粗糙齿面油膜压力作用下的齿根应力分析

2013-10-17亓秀梅高创宽

制造业自动化 2013年22期

秦亮，亓秀梅，高创宽

QIN Liang1,QI Xiu-mei1,GAO Chuang-kuan2

（太原理工大学机械工程学院，太原 030024；2. 杭州万向职业技术学院，杭州 310023)

0 引言

齿轮传动应用广泛，在机械传动中具有重要的地位。齿轮设计是以齿面接触疲劳强度及齿根弯曲疲劳强度为设计准则进行尺寸计算和校核。传统的设计方法设计周期长，效率低并与齿轮传动的实际工况有一定差异，因为绝大多数齿轮传动都在混合润滑状态下工作，即接触载荷由润滑油膜和齿面粗糙峰的直接碰撞共同承担。这样作用在每个啮合点的齿面接触载荷必然是随机分布载荷。近年来，一些学者借助ANSYS软件的强大分析功能及求解功能分析了齿轮弯曲应力[1～6]，但分析过程中并未考虑润滑作用。2010年，张延化和王优强[7]分析了油膜压力作用下的齿根弯曲应力，然而仍未计及齿面粗糙度效应。

本文首先基于实测所得试件的表面粗糙度数据，得出其数学模型；再利用多重网格法、多重网格积分法、逐列扫描法求得了油膜压力；然后，在Pro/E中基于参数化功能进行三维实体模型的建立，并将齿轮实体模型导入ANSYS中进行有限元分析求解，获得了真实粗糙齿面在混合弹流润滑状况下的齿轮弯曲疲劳强度的情况。从理论上探讨了润滑油膜与齿面粗糙度对齿轮弯曲疲劳强度的综合影响。

1 粗糙齿面压力分布计算

1.1 基本方程

1.1.1 Reynolds方程

润滑剂选Ree-Eyring型非牛顿流体，其非稳态线接触弹流润滑的Reynolds方程为[8]：

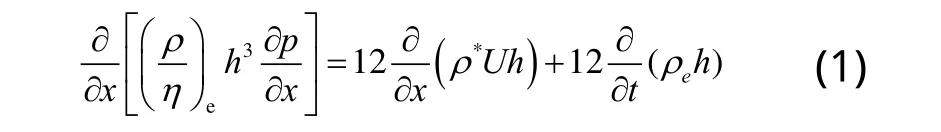
Reynolds方程的边界条件为：

式中，xin、xout分别为计算域始、终点坐标。

1.1.2 油膜厚度方程

假设齿轮a为粗糙齿面，齿轮b为光滑齿面，则齿面间的油膜厚度为：

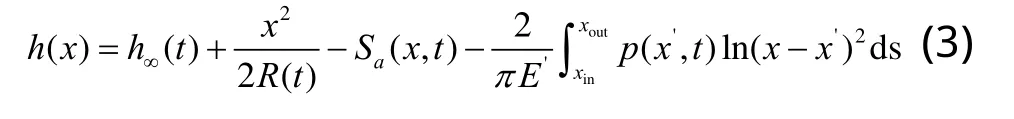
式中，h∞(t)—刚体中心膜厚；

R( t)—啮合点处的综合曲率半径；

Sa(x,t)—齿面a的粗糙度函数；

E'— 两轮齿材料的综合弹性模量。

本文应用Taylor Hobson公司生产的粗糙度轮廓测量分析仪，选用轮廓算术平均偏差Ra=0.26（μm)的试块，测得其表面真实粗糙度数据；然后借助MATLAB中的Curve Fitting功能，利用快速傅立叶变换获得了形如下式的齿面粗糙度函数：

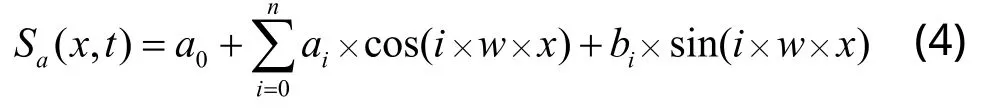
由式（4）可得粗糙度函数曲线如图1所示。

图1 粗糙度函数曲线

1.1.3 黏度方程

需要说明的是，基本方程中还包括密度方程、能量方程、热传导方程及载荷方程等，其推导与建立详见文献[8,9] ，在此不再赘述。

1.2 粗糙齿面油膜压力计算示例

某工业齿轮传动及其所用润滑剂参数如表1所示。

表1 齿轮传动及润滑剂基本参数

基于表1中参数，采用多重网格法、多重网格积分法、逐列扫描法[8]获得了沿齿轮传动啮合线五个特殊点：啮入点、双齿变单齿、节点、单齿变双齿、啮出点处的粗糙齿面油膜压力分布。图2为五个特殊啮合点处的计算结果。

图2 五个特殊点处齿面油膜压力分布

2 齿轮建模及有限元分析

2.1 齿轮参数化建模

在齿轮三维建模中，轮廓渐开线的生成是最核心、最重要的环节，齿轮模型的准确与否直接影响到有限元计算结果的正确性。本文在Pro/E中进行了齿轮参数化建模，在Pro/E中根据式（6）所示方程绘制了渐开线曲线，创建完整的齿轮模型。应用Pro/E的全参数化特性，可直接修改参数值，再生之后，生成另一齿轮。

2.2 ANSYS有限元分析

鉴于本文的载荷施加区为单个轮齿的Hertz区域，且计算所关注的区域仅为轮齿的齿根部位。根据圣维南原理，可只取整个齿轮模型的3个轮齿作为研究对象。简化后的计算模型如图3所示。本文将Pro/E文件以IGES保存，并在ANSYS中通过Import导入文件。

图3 简化的齿轮三维模型

2.2.1 前处理

选择单元类型为solid185，定义材料弹性模量和泊松比分别为2.1E5 (MPa)与0.28。利用辅助圆柱面使其分为两部分，采用体扫掠生成网格，最终生成了160280个单元、173102个节点。生成后的网格如图4所示。

图4 网格划分

对齿轮轴孔圆柱面施加全约束，两个切割面施加对称约束。齿轮在传动中，理论上为线接触，但因在齿面压力作用下会产生弹性变形，故将加载区域设置成宽为两个Hertz半宽的狭窄接触带，在区间表面施加如前计算所得的粗糙齿面油膜压力。

2.2.2 求解及后处理

下文以轮齿在节点啮合为例进行阐述。对齿轮进行静力学分析，应力云图如图5所示，可见最大应力在加载处，最大等效应力值为652.261(MPa)，最大位移为0.042 (mm)。

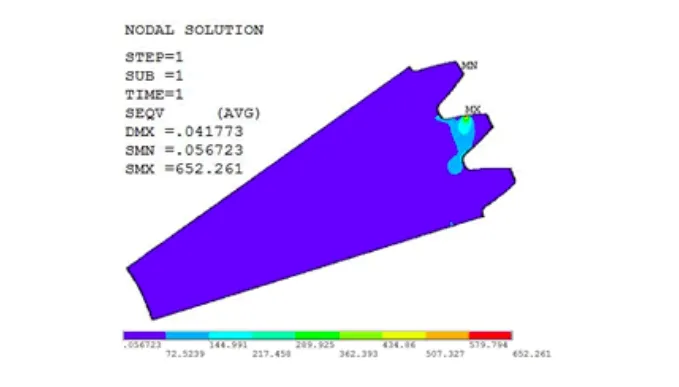
图5 齿轮应力云图

2.2.3 五个特殊啮合点处计算结果比较与分析

对于表1所给齿轮传动，沿其传动啮合线五个特殊啮合点处的计算结果如表2所示。

表2 五个特殊点的计算结果

为了获取不同齿轮模型的计算结果，本文在完成上述算例的基础上又进行了两个算例的计算。两个算例计算的绝大多数输入参数维持表1所给参数不变，仅对少数参数做了变动，变动条件分别如下：算例2的变动参数为：齿数分别为50、200，模数为10（mm），小齿轮转速为446.7244(r.p.m)，单位齿宽载荷为1.2072×106(N/m)；算例3的变动参数为：齿数分别为30、60，模数为 10（mm），小齿轮转速744.5407 (r.p.m)，单位齿宽载荷为6.0358×105(N/m)。计算结果分别列于表3和表4中。