流体遇障碍物后流动的初步发展数值模拟

张俊婷，崔小朝，王宥宏

(太原科技大学应用科学学院，太原 030024)

绕流在实际工程中的应用是十分广泛的，在众多工程领域如:能源环境、机械航空、土木、水利、海洋等，都具有非常重要的现实意义。例如水流对渡槽槽墩、桥梁、海洋钻井平台支柱、海底输运管线、桩基码头等作用引起的振动和局部冲刷，均与绕流引起的分离、不稳定尾流、局部复杂流动结构密切相关[1-3]。流体流经不同结构的物体时会形成复杂且不稳定的分离及尾流结构，尽管已有一个多世纪的研究历史，但是迄今对该流动现象物理本质的理解仍不完整，绕流依然是流体力学中具有挑战性的课题[4-5]。

随着计算机的快速发展，数值模拟逐渐成为重要的研究手段。人们曾使用多种数值方法，如直接数值模拟法(DNS)、大涡模拟法(LES)、求解雷诺平均 N-S方程(加湍流模型，如 k-ε 模型)[6-12]等对各种各样的流体绕流问题进行研究，但相关理论研究成果较贫乏，进行研究具有重要的基础理论意义。本文基于雷诺平均方程加湍流模型，利用Ansys软件对同一雷诺数下流体流经不同形状障碍物后流动的初步发展进行数值模拟，模拟了流场流经四种不同形状障碍物的绕流问题，分析了流体流经不同形状障碍物的流场，同时比较了不同来流速度下流体流经障碍物的流场变化，了解其流动机理和水动力规律，并希望对工程实际具有一定的指导意义。

1 数学模型

1.1 控制方程

连续性方程:

动量守恒方程:

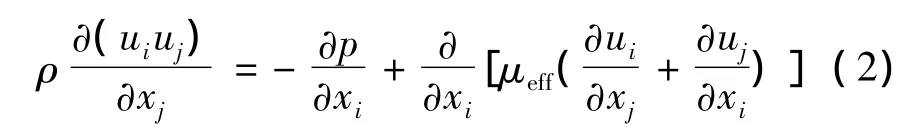
能量方程:

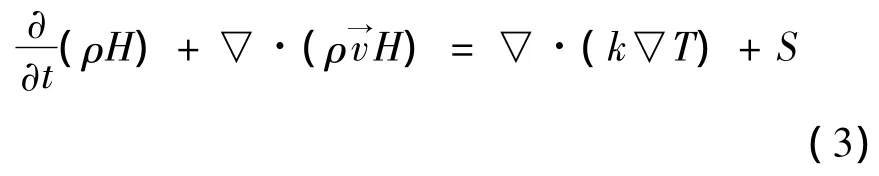
其中:

H——材料的热焓:H=h+△H;

S——源项，无内热源时其值为0.

采用标准k-ε双方程模型来描述明渠的湍流流动，其对应的输运方程如下:

湍动能方程:

k—— 湍动能;

ε——湍动能耗散率;

μeff—— 有效粘度系数;

Gk——由于平均速度梯度引起的湍动能k的产生项。

1.2 模型的建立

本文主要分析了流体流经四种形状障碍物后的流动发展情况，并将问题简化为平面模型，利用ANSYS11.0软件建模分析，表1为四种形状障碍物的水力半径:

表1 四种模型的水力半径Tab.1 The hydraulic radius of four kinds of molds

设dh相同，有Re=，这样就可以使流体流通过不同形状障碍物雷诺数相同，从而得到相同雷诺数下不同形状的障碍物对流体流动的影响。

1.3 边界条件

(1)入口边界条件

在本模拟计算中将入口边界设置为进口来流速度，根据湍流模式选取了3种来流速度;而且使用SFE和SFL命令设置了湿润边界。

(2)出口边界条件

在水流流动过程中，没做任何设置，默认为自由流动。

(3)底层壁面条件

在水流流动过程中，设置水流速度设为0.

2 模拟结果分析

由图1可以看出，当流体以0.3 m/s的速度流经障碍物时，在不同位置处其流速不同。当流体流经障碍物的前半部时，由于压强沿流动方向逐渐降低，流体质点的速度得到提高;当流体越过障碍物的最高位置流经其后半部时，流体的势能变小并转换为动能，流体的速度也进一步增大。在图1(a)-图1(d)中，流体的主体流线基本类似。但图1(d)在矩形障碍的下游处产生明显的回流区，即在矩形障碍的尖角点处发生了边界层分离。

图2为流体以0.6 m/s的速度流经障碍物时的流场分布，其中图2(a)和图2(b)中流体的流线相似，并且从图中还可以发现在障碍物的最高处边界层的速度达到最大，同时流体在障碍物尖角处发生边界层分离，在该处流体质点的速度几乎为零。而在图2(c)和图2(d)中，在越过障碍流经障碍物的下半部时处均产生明显的回流区，与图1(c)和图1(d)中的回流区域相比，图2(c)和图2(d)中产生的回流区域变大，特别地对于三角形障碍物来讲，该变化更加显著。

图3为速度为1.5 m/s时，流体流经障碍物的流场分布。比较图1、图2及图3，发现随着速度的增大，流体越过障碍物后的主流速度也提高。一方面是因为在障碍物前半部由于压强沿流动方向在减小，从而提高了流体质点的速度;另一方面由于在流体流过障碍物的最高点后流体的势能逐渐减小，动能逐渐增加，流体的速度进一步得到增加。另外，随着来流速度的提高，流经障碍物的流体在障碍物的后半部产生面积越来越大的回流区。分析其原因可能是随着来流速度的增大，在流体流经障碍物的后半部时产生的逆压梯度也越大，致使更多的被阻滞流体质点被迫停滞和倒退，同近壁处的流体质点一同堆积在障碍物表面和主流之间，使边界层剧烈增厚，同时边界层的流体质点的倒流也迅速扩展。

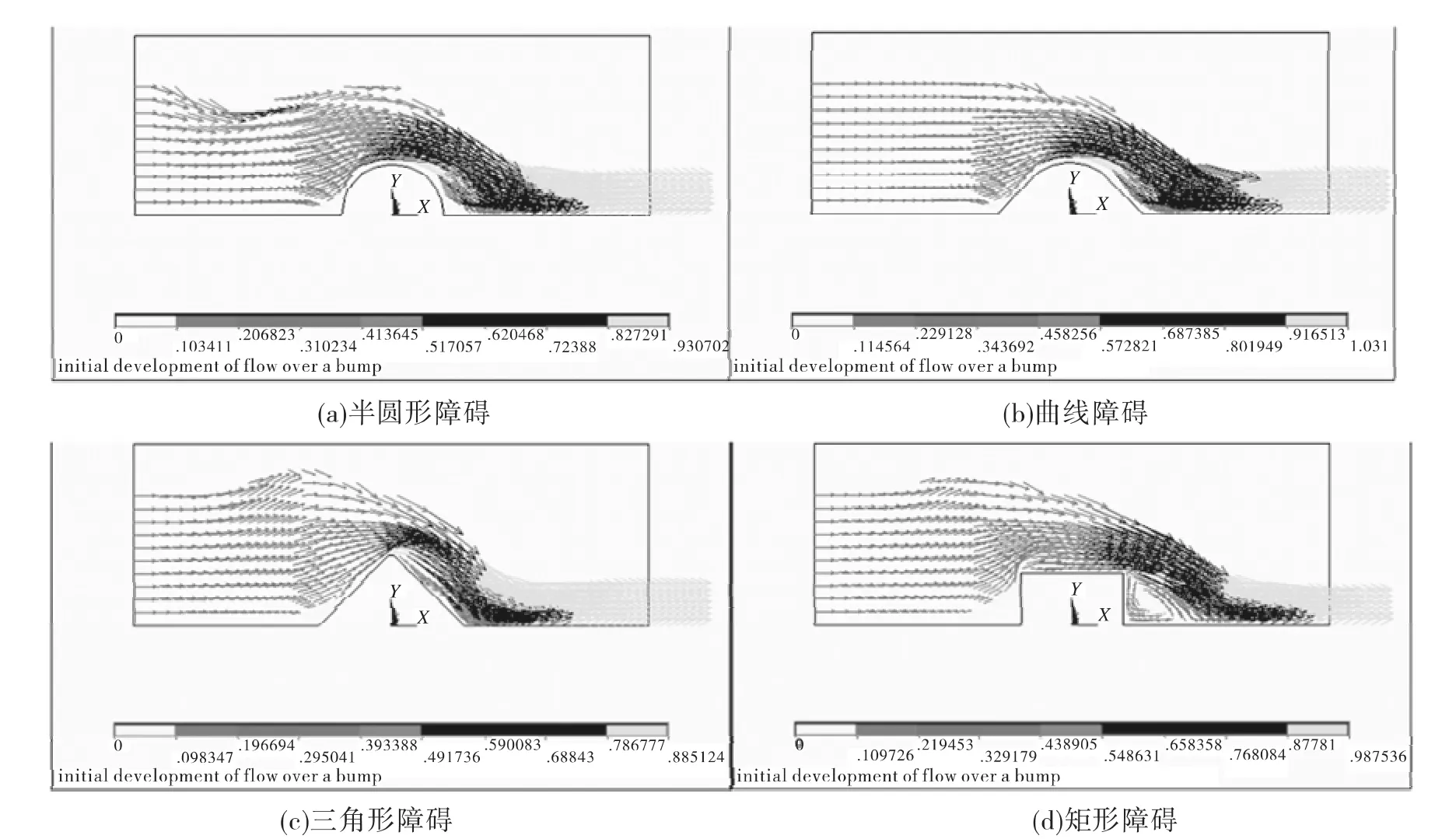
图1 速度为0.3 m/s时的流场分布Fig.1 The distribution of the flow field at the velocity of 0.3 m/s

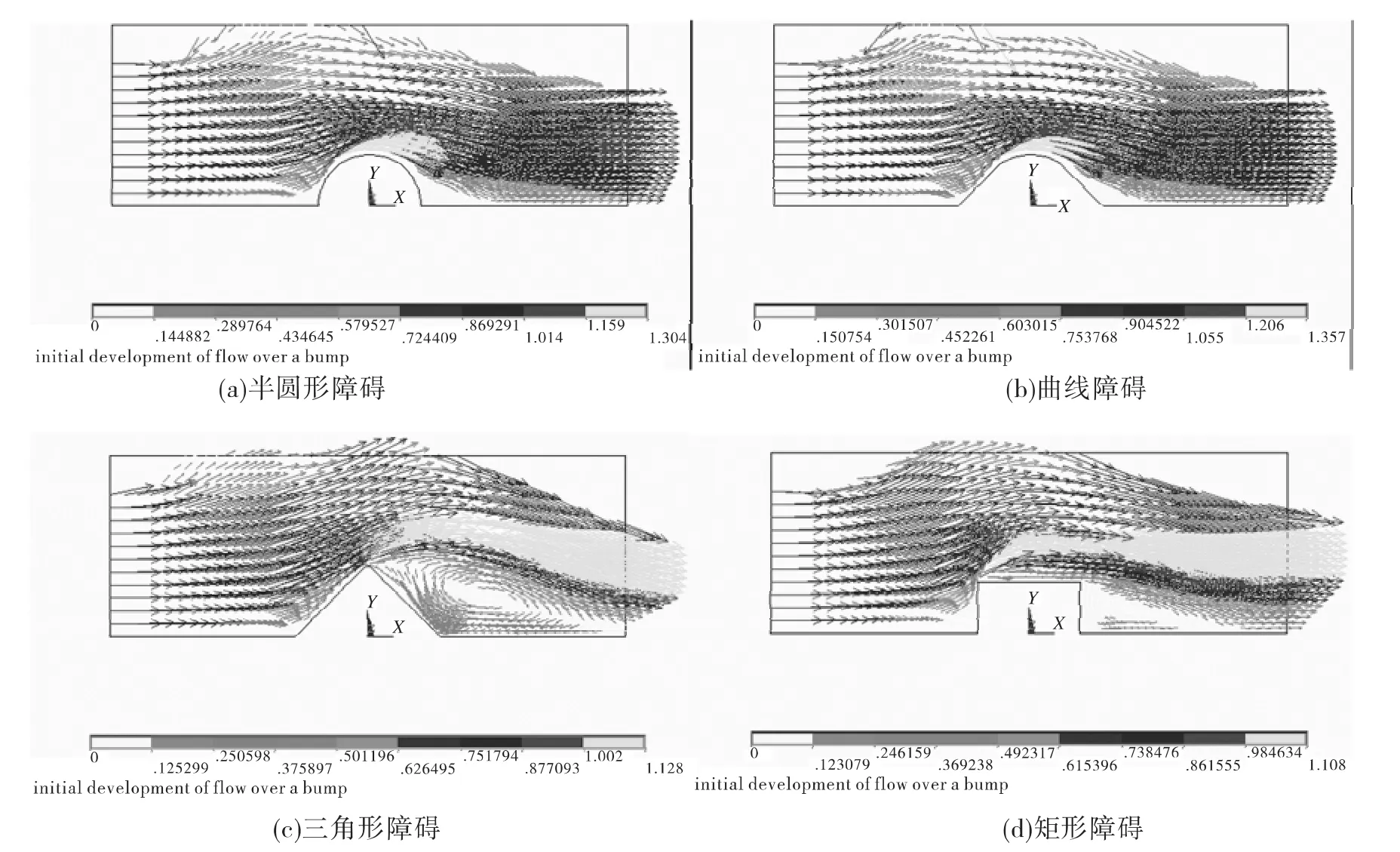
图2 速度为0.9 m/s时的流场分布Fig.2 The distribution of the flow field at the velocity of 0.9 m/s

3 结论

随着来流速度的提高，流体越过障碍物后的主流速度也提高，且对于不同形状的障碍物，均出现了不同区域大小的边界层分离区，即回流现象，并且对于半圆形障碍和曲线障碍，边界层分离出现在障碍的角点位置附近，而对于三角形障碍和矩形障碍来讲，当流体越过其最高点位置处即出现边界层分离，且出现的边界层分离区域也较大，该模拟结果与边界层理论相一致。

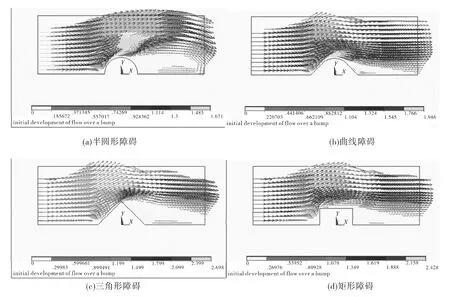
图3 速度为1.5 m/s时的流场分布Fig.3 The distribution of the flow field at the velocity of 1.5 m/s

[1]ZDRAVKOVICH M.Flow around circular cylinders:applications[M].2nd ed.UK:Oxford university Press，2002.

[2]SUMER B M，FREDSOE J.Hydrodynamics around cylindrical structures:advanced series on ocean engineering[M].Singapore:World Scientific，1997.

[3]李玲，李玉梁，祁雪春，等.浅水层圆柱绕流流动模式的实验研究[J].自然科学进展，2000，10(6):554-559.

[4]WILLIAMSON C H K.Vortex dynamics in the cylinder wake[J].Annual Review of Fluid Mechanics，1996，28:477-539.

[5]ZDRAVKOVICH M.Flow around circular cylinders:fundamentals[M].England:Oxford University Press，1997.

[6]TUTAR M，HOLDOB A E.Computational modeling of flow around a circular cylinder in sub-critical flow regime with various turbulence models[J].Int J Numer Meth Fluids 2001，35:763-784.

[7]KARABELAS S J.Large-Eddy simulation of high-Reynolds number flow past a rotating cylinder[J].International Journal of Heat and Fluid Flow，2010，31(3):518-527.

[8]魏英杰，何钟怡.槽道中方形障碍物绕流的大涡模拟[J].水动力学研究与进展，2003，18(4):433-438.

[9]姚育成，李万平，李良军.高雷诺数情况下钝体绕流的数值模拟[J].华中科技大学学报:自然科学版，2003，31(2):106-108.

[10]郝鹏，李国栋，杨兰，等.圆柱绕流流场结构的大涡模拟研究[J].应用力学学报，2012，29(4):437-443.

[11]姚熊亮，方媛媛，戴绍仕，等.基于LES方法圆柱绕流三维数值模拟[J].水动力学研究与进展，2009，2(5):564-572.

[12]常书平，王永生，庞之洋.用基于SST模型的DES方法数值模拟圆柱绕流[J].舰船科学技术，2009，31(2):30-33.