B样条曲面变形方法的设计与实现
2013-10-16朱美玲董玲珍
朱美玲,董玲珍
(1.太原城市职业技术学院,太原 030027;2.太原理工大学理学院,太原 030024)
曲面造型是计算机辅助设计(CAD)和计算机图形学(CG)领域最活跃、关键的学科分支之一[1-2]。目前,计算机中的表面建模技术被不同的应用领域所需求[3]。为满足不同的应用需求,基于不同的表示方法发展衍生了相应的曲面造型技术。根据曲面变形的机理可大致分为4类[4-5]:基于几何模型的曲面变形、自由变形(FFD)、基于物理模型的变形方法和基于几何约束优化的变形。B样条曲面作为一种应用广泛的逼近样条类,它允许曲面可以局部控制,同时因为样条曲面是线性连续且光滑的曲面,所以用样条曲面来定义变形的参数空间可以使变形更加精确。
本文首先介绍了双三次B样条曲面的变形基础和曲面拼接的表达式,提出了一种双三次B样条曲面生成的改进算法,然后采用点约束、目标曲线约束两种几何约束驱动双三次B样条曲面变形,在点约束求解中以控制节点位移最小为目标函数,使用LINGO软件计算得到该目标下的最优解,并给出计算实例验证了该方法的可行性。
1 变形基础
1.1 双三次B样条曲面
一个双三次B样条曲面用下面的等式来表示:
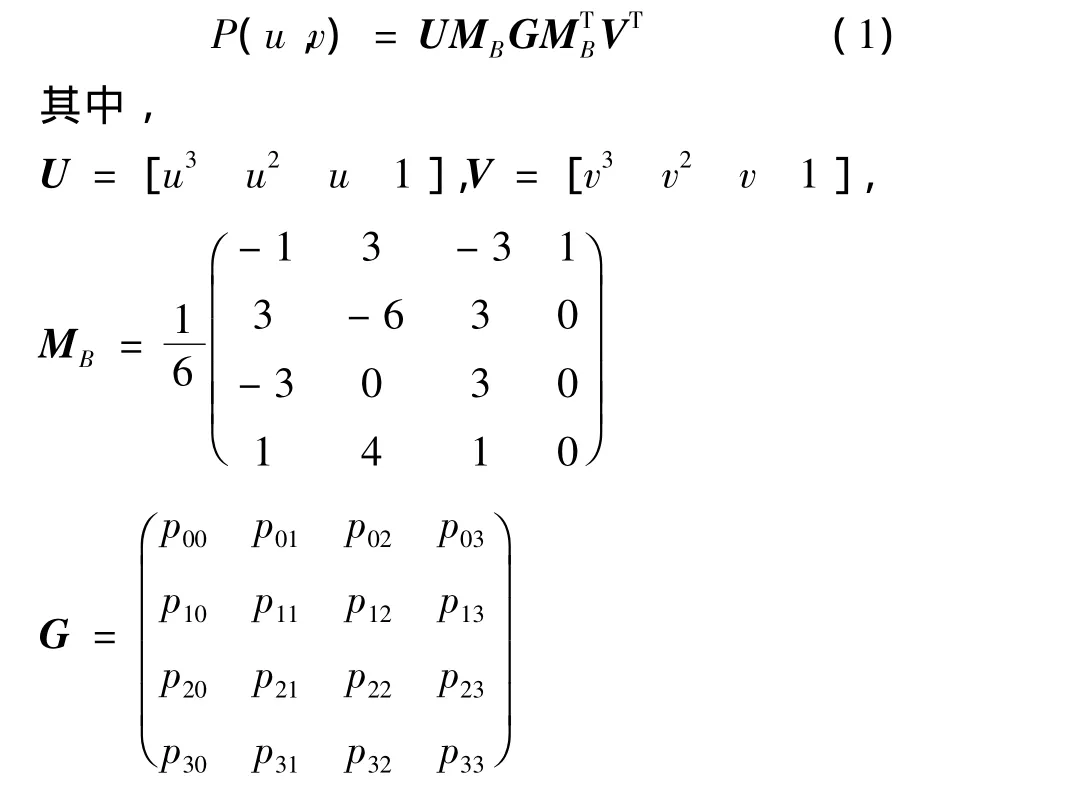
式中,G代表控制节点矩阵。
等式(1)也可用如下等式来表示:

使用方程(2),当u和v由0到1改变时,能够生成一个双三次B样条曲面,它能有效地提高生成效率。图1为一个双三次B样条曲面的例子。
1.2 曲面拼接

图1 双三次B样条曲面Fig.1 Three B-spline surfaces
为了实现双三次B样条曲面拼接,扩展控制节点矩阵G,然后以每次4×4的方式获取单面的控制节点矩阵来拼接。下面是一个控制节点矩阵。
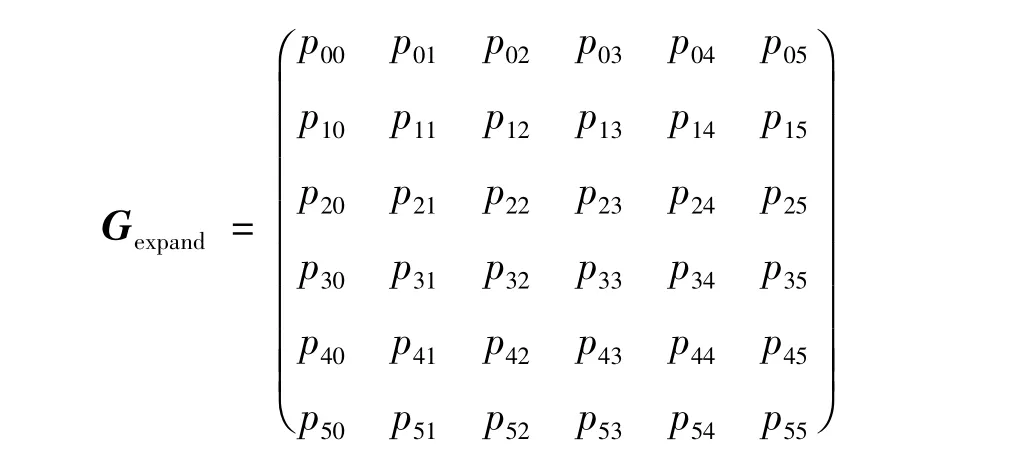
拼接完Gexpand后,获得了9个4×4的控制节点矩阵。图2表示了在这个合成曲面中单面位置。

图2 单面和合成面的关系Fig.2 The relationship between single surface and synthesis surface
这个合成面在变形过程中始终保持C2的连续性。如图3所示。

图3 改变控制节点后的变形Fig.3 The deformation after change control nodes
2 几何约束及其求解
目前主要有两种常用的几何约束用于变形操作:离散约束和连续约束。其中离散约束包括空间点信息、控制顶点位移等,连续约束包括曲线和子曲面等。由于连续约束的处理将给求解引入非线性的约束,使得变形过程复杂且难以收敛,因此主要关注离散约束类型,连续约束可通过离散采样等方法转化为一般的离散约束类型。
2.1 点约束及其求解
在平面上点pm(u,v)处,位置约束(2)和切线约束(3)形成了基本约束,能够被写成[6]:

其中N=(A,B,C)是变形后曲面在pt上的法向量,Pt为目标点。
考虑方程(1)和点约束,因而,目标是计算一个新的控制节点矩阵。

节点控制矩阵是4×4方阵,考虑到未知量的个数和曲面变形的效果,将控制节点矩阵中4个坐标值设为变量,其余12个坐标值保持固定,变形问题在各个维度上就转换为求解4元一次方程组的问题,所以是以最小控制节点位移求解的最佳模型。为了降低复杂度,在变形过程中设 Px10,Px11,Px12,Px13是变量,其他的都是固定值。这样,点约束的求解转变成线性等式的求解。在点约束下,沿着坐标y轴,得到等式(4)。
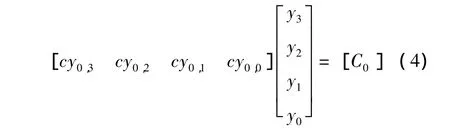
建立以最小控制节点位移求解的最佳模型。使用LINGO计算新的控制节点解。图4展示了求解节点约束解的过程。
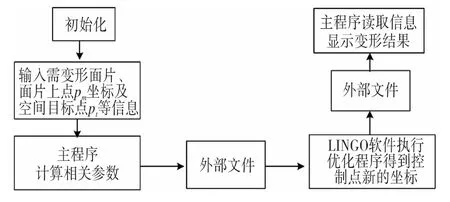
图4 点约束的求解过程Fig.4 The solving process of point constraint
2.2 目标曲线约束及其求解
目标曲线约束是一种连续的约束,解决这种约束将给系统引入非线性约束,会使得解决过程复杂而且难以聚合[7]。因此,在解决这种约束之前,先分离目标曲线为离散的点,然后像解决多个点约束一样解决它。比较等式(4),在目标曲线约束下我们沿着y轴能够获得等式(5).
式中,AY表示系数矩阵,AYb表示常数矩阵,则(5)可以表示为:

使用最小二乘法得到等式(7):

其中NAY=AYT×AY,并且有:
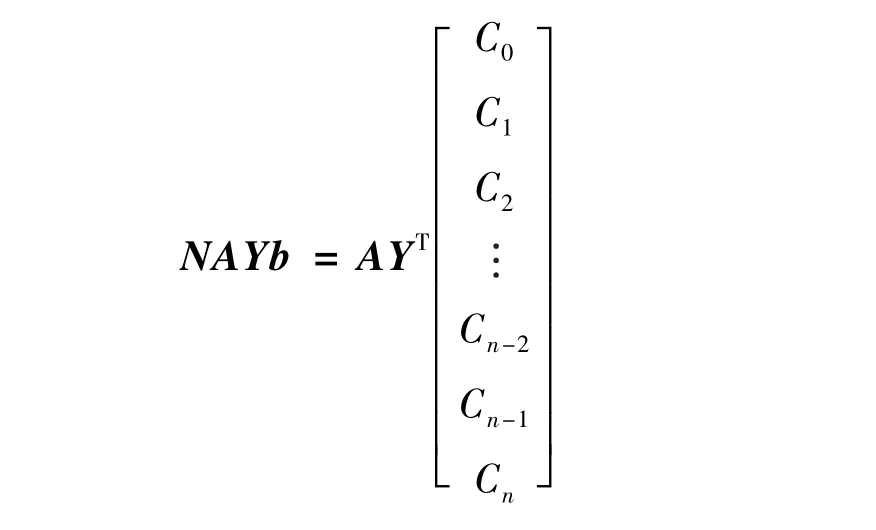
如果NAY是可逆,则:y=NAY-1·NAYb
否则:y=NAY+·NAYb
其中NAY+是矩阵NAY的伪逆。
3 求解几何约束实例
3.1 点约束求解的例子
输入需变形的曲面面片5(如图2)上的点以及目标点,利用如图4所示的求解过程,求解3个例子。
例1:
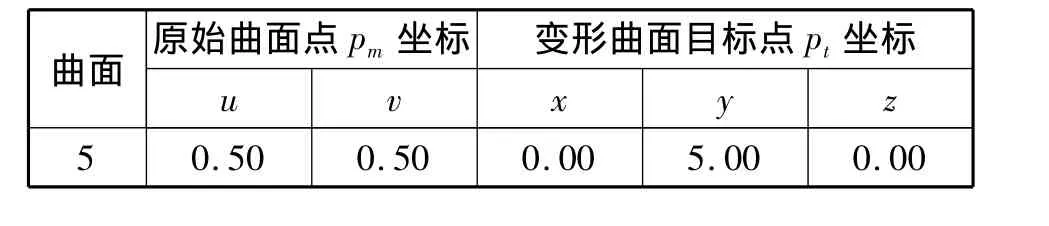
表1 变形信息Tab.1 The deformation information

图5 求解点约束(例1)Fig.5 The solving point constraint(example 1)
图5展示了表1给出的变形信息,即面片5上点 pm(0.50,0.50)变形到空间点 pt(0.00,5.00,0.00)的变形结果。
例2:
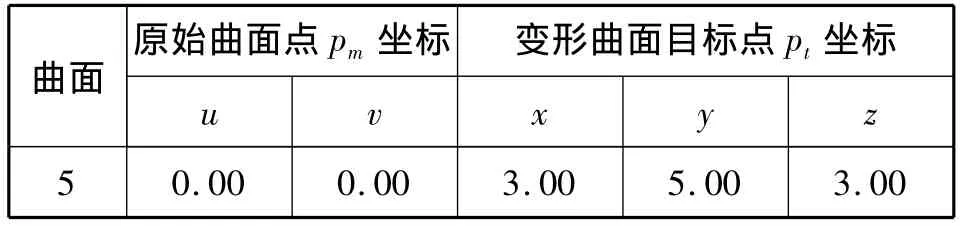
表2 变形信息Tab.2 Deformation information

图6 点约束求解(例2)Fig.6 Solving point constraint(example 2)
图6展示了表2给出的变形信息,即面片5上点 pm(0.00,0.00)变形到空间点 pt(3.00,5.00,3.00)的变形结果。
图7展示了表3给出的变形信息,即面片5上点 pm(0.80,0.90)变形到空间点 pt(3.00,5.00,3.00)的变形结果。图5-图7给出了以控制节点最小位移求解点约束目标方程的结果。

图8 求解目标曲线约束(例4)Fig.8 Solving point constraint(example 4)
例3:

表3 变形信息Tab.3 Deformation information

图7 求解点约束(例3)Fig.7 Solving point constraint(example 3)
3.2 求解目标曲线约束例子
如图8(a)所示,在原始曲面面片上选取5个目标点,将目标曲线离散为5个点(用红色绘制),通过MATLAB获得变形结果。
例4:
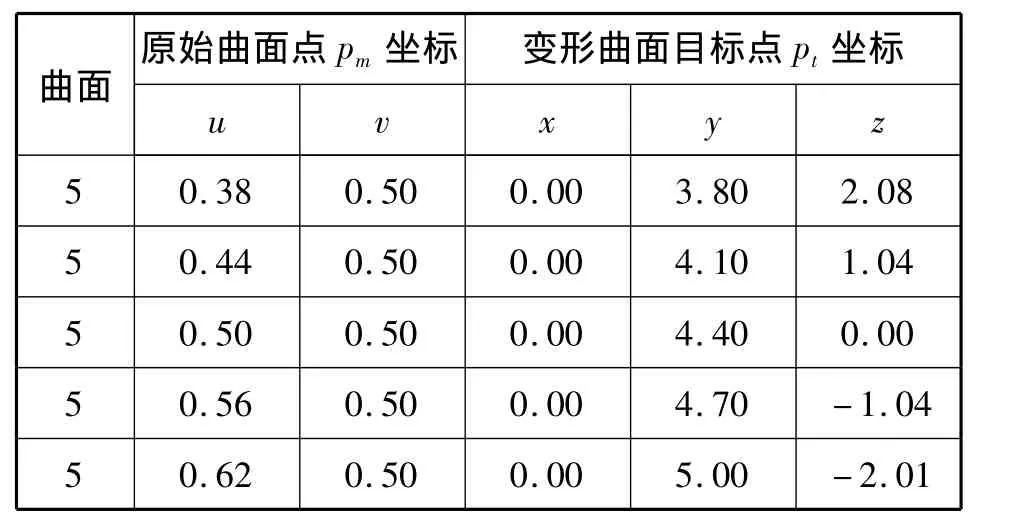
表4 变形信息Tab.4 Deformation information
从图8(b)及图8(c)中可以看出随着单个面片向着目标曲线趋近时,与其拼接的曲面也都相应的发生改变最终维持了整个复合曲面的C2连续性。
在图9中可以看出,需要变形的曲面没有完全通过第1、3、5个目标点,而较好的通过第2、4个目标点。
例5:

表5 变形信息Tab.5 Deformation information

图9 求解目标曲线约束(例5)Fig.9 The constraint of solving point(example 5)
4 结论
文章论述了以几何约束来驱动双三次B样条曲面。双三次B样条曲面采用矩阵的表达形式。在这一基础上对控制节点矩阵进行扩充,并且按照4×4的规模进行分割从而实现双三次B样条曲面的拼接。各个曲面面片拼接后满足C2连续度。之后,对几何约束,包括点约束,目标曲线约束进行分析。开发系统能够完成接收变形曲面面片标号,面片上的点以及空间目标点等用户输入信息,计算参数,调用LINGO程序进行计算,展示变形结果等功能。在目标曲线约束求解中借助MATLAB,模拟得到变形结果。但还应进一步研究其它一些约束表达与实现(如目标曲线的切线约束等),开发以点约束驱动曲面变形的程序,使其能够实现用鼠标拾取曲面上点,拖动鼠标实现曲面的变形。
[1]LI HAN,FAFFAELE DE AMICIS,etal.Interactive B-spline Surface Modeling based on Force Density Method[J].Journal of Image and Graphics,2009,14(9):1900-1907.
[2]CHEN YUEPING,LI SHUPING,SHENYANHUI,et al.Key technology study on generating bi-cubic B-spline surface[J].Machinery Design & Manufacture,2010(4):225-228.
[3]GUILLET S,LEON J C.Parametrically deformed free-form surfaces as part of a variational model[J].Computer Aided Design,1998,30(8):621-630.
[4]王青,柯映林,李江雄.基于力密度方法的NURBS曲线和曲面变形框架[J].机械工程学报,2007,43(3):135-142.
[5]NEALEN A,IGARASHI T,SORKINE O,et al.Laplacianmesh optimization[C]∥Proceedings of ACM GRAPHITE,2006:381-389.
[6]HU S S,ZHU Q X.Stochastic Optimal Control and Analysis of Stability of Networked Control Systems with long delay[J].Automatica.2003,39(11):1877-1884.
[7]BAUER P H,SICHITIU M.Total Delay Compensation in LAN Control Systems and Implications for Scheduling[J].Proc of the American Control Conference,Arlington,2001(6):4300-4305.
