用插值函数绘制离心泵叶片流线展开图

胡家顺 王 冕 杨 明 董 川 熊 勃

（武汉工程大学机电工程学院)

在叶轮的绘型中，当完成流线的分点后需将流线在方格网图上展开。传统的绘制方法是用弹性较好的软尺，弯折其两端使与流线的入、出口安装角相等，按软尺自然形成的曲线绘出。若按此绘出的展开流线前后角度不平缓时，需修改叶片入口边在轴面投影图上的位置，再绘制流线的展开图，直到符合要求为止。可见该方法误差大、效率低。

因此不少研究者对此提出了改进的方法，如文献 [1] 给出的用样条函数和文献 [2] 给出的用贝赛尔曲线绘制流线展开图的方法都十分方便有效，但均有数值计算量偏大之疵。

本文给出了一种用n次插值函数绘制离心泵叶片流线展开图的方法。利用该方法绘制叶片流线展开图，可通过选择不同的插值节点，方便地控制或改变叶片流线展开图形，以满足不同的设计要求。

1 一元n点插值函数的构成

当已知n个点时，可以通过全部n个点作一插值函数P（x），如式 （1）所示，可以用它求其任意节点间的函数插值。

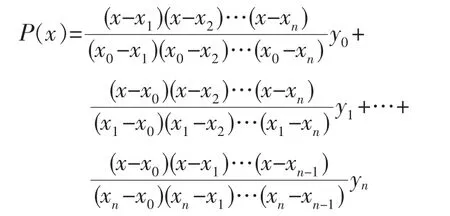
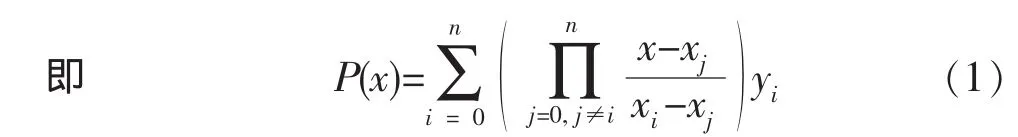
一元n点插值函数，虽然在应用时十分方便，但由于该插值函数为一高次方程，特别是当n值很大时（节点数很多时)，可能出现插值的不稳定性。为避其弊端，现取n=4构成插值函数，用以绘制叶片流线展开图。插值函数的具体表达式如下式所示。

其一阶导数为

2 插值函数节点的确定

2.1 节点0、1、3、4的确定

节点0(x0，y0)和节点4(x4，y4)可选在流线的进出口的两个端点上 （见图1），即

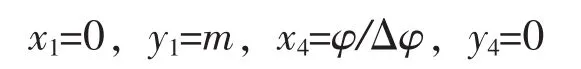
式中m——流线在入口边处的分点序号；

φ——叶片包角；

Δφ——任意轴面间夹角。

为使流线两端点处满足

可将节点1(x1，y1)和节点3(x3，y3)分别选在流线进出口安装夹角 β1和 β2的射线 l1和 l3上 （见图1）。笔者经大量算例表明，当取

时，流线能较好地满足式 （4）、式 （5）所给出的条件，且各流线在距出口端约20°～30°时具有趋于重合的特性。x1、x3确定后，y1、y3可按下式计算:

2.2 节点2的确定

由式 （4）、式 （5）给出的流线两个端点处的边界条件，可分别解得

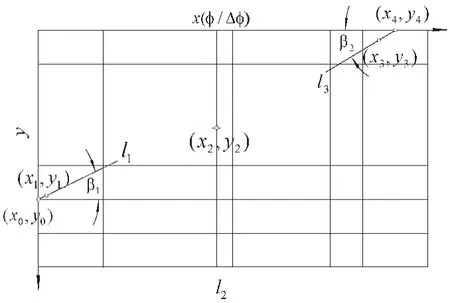
图1 n=4插值函数节点确定的示意图

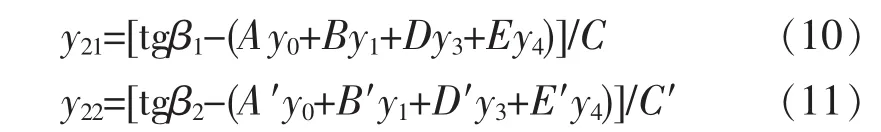
其 中 A、 B、 C、 D、 E分 别 为 x=x0时 ， i=0， 1， 2， 3， 4 的

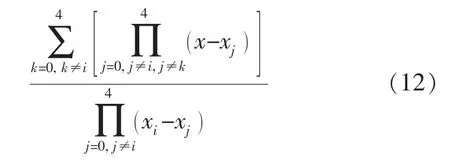
值； A′、 B′、C′、 D′、 E′分别为 x=x4时 ， i=0， 1，2， 3，4 的

值。y21应等于y22，即

这是一个以x2为未知量的非线性方程，可用数值方法求解得x2后代回到式 （10）或式 （11），便可求得y2。由于用数值方法求解方程 （14）过于繁复，为简化计算，在按式（6）～式（9）确定节点1、3后，可将节点2的x2值取为x0、x4的中点，即

而将y2取为

经笔者大量算例表明，用上述简化方法确定的节点所构成的插值函数来绘制流线展开图，均获得较为满意的结果。

3 计算实例

某电解液循环泵叶轮的绘型中，已知叶片流线进口处的分点值及进出口安装角 （见表1），叶片包角及任意轴面间夹角为=110°、 Δφ=5°。

表1 叶片流线分点值及进出口安装角

先确定绘制前盖板流线a插值函数的节点。

节点0： 取x0=0，y0=9.34；

节点 4： 取 x4=φ/Δφ=110°/5°=22， y4=0；

节点1：按式 (6)取 x1=0.01，

节点3：按式 (7)取x3=0.95x4=21，

其中 A′、 B′、 C′、 D′、 E′由式 (13) 计算得到：

将上述数值及y0、y1、y3、y4值一并代入上式得

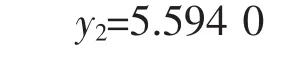
后盖板流线b和中间流线c插值函数的节点确定方法同上。表2列出了各流线插值函数的节点以及由这些节点所构成的插值函数一阶导数在两个端点上的值。

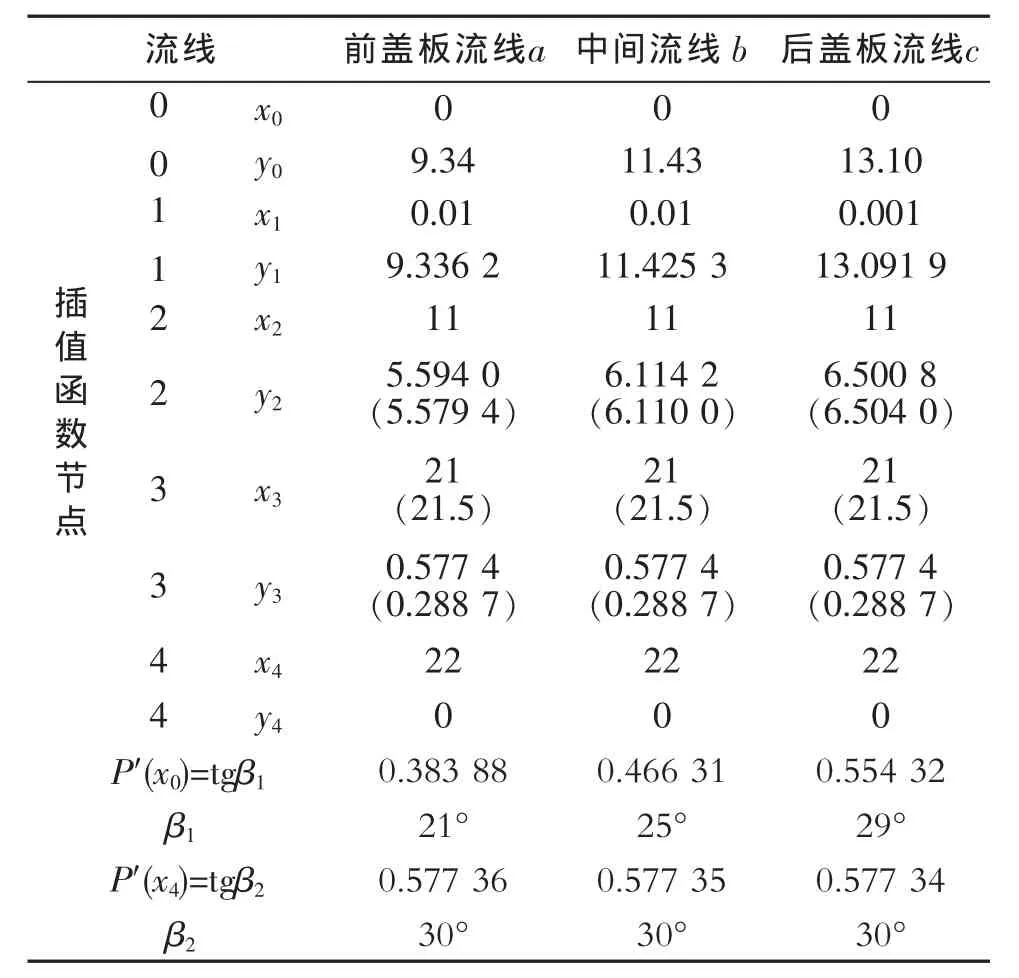
表2 插值函数节点值

在确定了各流线的插值函数的节点后可按式(2)分别计算各不同x值时的P（x），得到一系列点（x，P（x）），连接这些点即得各流线的展开图，其结果见图2。

图2 Q25H58电解液循环泵叶片流线展开图之一

将表2中节点3的x3值取为21.5而其他条件均保持不变，据此绘出的各流线展开图如图3所示。 比较图2、 图3可见， 在90°～110°（即x=18～22）处有明显的差异，图2上各流线在此范围的重合度较之图3的要高，也更符合离心泵叶片流线在出口处的走向特性。

图3 Q25H58电解液循环泵叶片流线展开图之二

由此可见，用插值函数绘制叶片流线展开图，通过选择不同的插值节点，即能方便地控制或改变叶片流线展开图形，以获得满意的结果。

[1] 陈世亮.叶片流线展开的计算方法 [J] .流体工程，1992 （2）： 44-45.

[2] 谢俊.贝赛尔曲线设计离心泵叶轮的叶片型线 [J] .排灌机械， 2000， 18 （4）： 1-3.