一种新的Q学习算法在机械臂轨迹规划中的应用

李艳辉,赵 辉,李珊珊

(东北石油大学 电气信息工程学院,黑龙江 大庆 163318)

0 引 言

机械臂轨迹规划是机器人学习的重要分支之一,已有不少学者对其进行了研究。具有代表性的PID (Proportion Integration Differentiation)策略,它可以控制柔性机械臂,实现干扰量快速补偿及系统偏差纠正,不足之处在于当控制对象发生变化时需要重新调整控制器参数[1]。在空间站机械臂系统中,当机械振动、电磁干扰等不确定性因素可估计时,自适应控制方式可有效地控制机械臂的稳定性[2]。文献[3,4]的智能控制策略将神经网络与TD (Temporal Differences)算法结合,能对变结构机械臂在线实时建模,可以实现轨迹最优。遗憾的是其引入两种学习方式,因耗时多而影响运行速度,对处理器和对象模型都提出了较高的要求。由此可知,研究兼具快速性和稳定性的机械臂控制策略将具有非常重要的实际工程意义。

Q学习是一种不依赖于对象模型,以实现优化决策序列为目的的智能算法[5]。近年来,已有不少学者研究了该算法在多移动机器人协同控制中的应用[6-8],而机械臂可视作由多个具有耦合关系的移动个体,通过共享知识,相互紧密协作构成。因此,可将Q学习算法应用于机械臂轨迹规划中。由于Q学习算法在搜索最优动作时易陷入局部最优解状态[9,10],所以,笔者提出一种新的对知识的探索----利用比例能进行合理分配的动态搜索Q学习算法,有效地增强了算法的决策能力； 同时,提出根据动作效果进行量化评判的函数,显著地提高了评价的公平性和客观性。仿真结果验证了该算法在机械臂轨迹规划中应用的可行性和有效性。

1 机械臂二维工作空间描述

机械臂轨迹规划目的是使其沿一条优化轨迹达到目标位置。根据机械臂结构特性,在忽略机械结构约束和连杆间轴向间距的前提下,假设机械臂首端连杆可以绕基座旋转180°。规定在任意时刻,机械臂以基座为圆心,r为半径的圆形区域内运动,该区域称为机械臂的work空间,在work中建立直角坐标系,以基座位置为原点,机械臂的工作空间如图1所示。

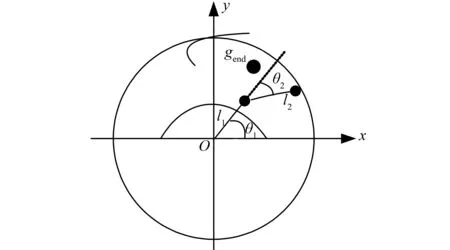
图1 机械臂工作空间示意图

设机械臂在[-π/2,π/2]范围内旋转,坐标gend(x,y)表示目标位置,其中

x=r*cos(φ),y=r*sin(φ)

(1)

其中φ=((rand()×2)-1)×π,rand为[0,1]间的随机数； 参数rmin≤r≤rmax,rmin=l1,rmax=l1+l2;p1(x1,y1),p2(x2,y2)分别表示连杆l1、l2的端点位置。目标点gend(x,y)的取值范围:{gend(x,y)|-rmax≤x≤rmax,rmin≤y≤rmax},由此可将目标位置限定在第1、2象限的扇形区域内。

2 基于Q学习的轨迹规划控制器设计

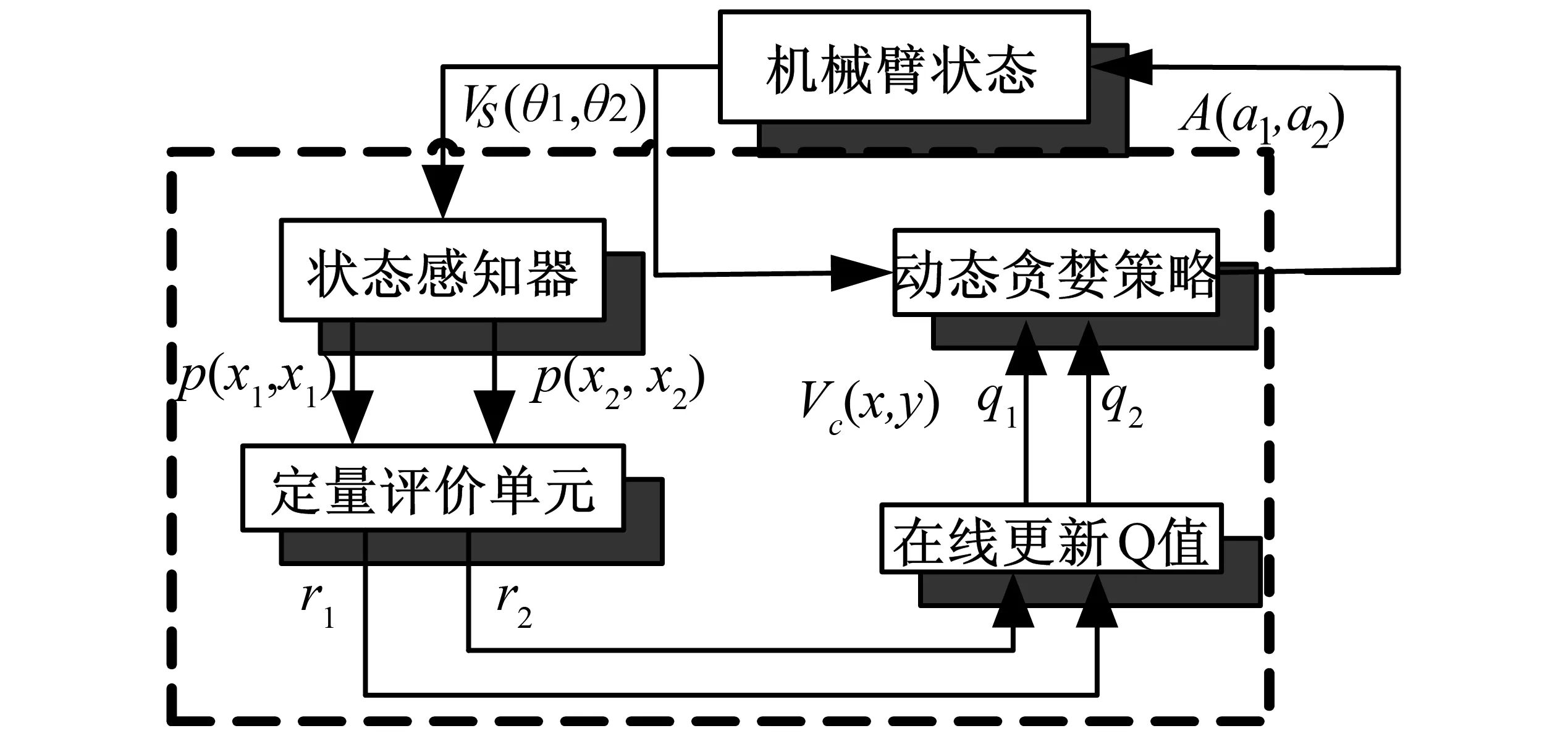
图2 控制器结构图

笔者设计的控制器依赖于强化学习原理,以在线试错的学习方式寻求最优动作策略,最终达到目标状态。控制器结构如图2中虚线框内4部分所示,状态感知器获得机械臂当前状态后,由定量评价单元对本次动作效果进行评价,同时在线更新机构累积学习经验,最后利用贪婪策略参考学习经验和状态,搜索最优动作并执行该动作。其中Vs(θ1,θ2)为角度向量,θ1,θ2分别为连杆l1,l2的偏移角；A(a1,a2)为动作向量,r1,r2为对应动作的立即回报值；q1,q2为两个连杆的动态更新的Q值。下面针对4个部分分别给出详细的设计原理。

2.1 状态感知器

状态感知器的作用是首先读取连杆l1,l2的角度位置,然后求得各端点的直角坐标,为定量评价单元和动态贪婪策略提供输入参数。端点坐标计算方法如下

(2)

式(2)分别用于确定连杆l1,l2的端点位置,规定θ1,θ2顺时针为负,逆时针为正,连杆l2的末端为当前位置。

2.2 动态贪婪策略

Q学习算法中采用贪婪策略(ε-greedy)搜索最优动作,其中ε代表知识的探索和利用之间比例,ε的大小影响着动作搜索效果,通常ε是经过大量实验找出较合适值,存在盲目性且搜索效果不佳。因此,笔者给出一种使ε能根据学习效果做出自适应调整的新动态贪婪策略。

根据ε值对算法的影响,学习之初应使探索占主要成分,随着学习及经验的积累,知识利用成分增加,这一过程ε应逐渐减小。经过大量实验验证,提出以学习次数k为自变量,ε(k)值为因变量的函数,使ε随着k变大而逐渐减小。函数表达式如下

(3)

其中M为学习次数。当k=1时,ε(k)≈1代表学习之初只探索不利用； 当k=M时,ε(M)≈0代表只利用不探索； 0.99防止了ε(k)取到边界值0或1无意义状态。函数ε(k)随k渐变的过程就是由探索向利用经验知识的过渡过程。

通过利用动态贪婪策略可使学习过程动态调整,较之传统的固定ε贪婪策略更具智能化,同时也避免了盲目性,提高了效率。最后,将根据动态贪婪策略搜索得到的最优动作a输出并执行该动作,其中a∈A={-0.5,-0.3,-0.1,0,0.1,0.3,0.5},单位为弧度值； 动态贪婪策略在选择动作之初,根据ε随机选择匹配动作,之后根据被选动作对当前状态的有效程度给予相应的概率分配,当进行下一状态选择动作时,动态贪婪策略根据前次搜索结果优先选择概率较大的动作,概率较小的动作次之； 在遍历所有动作后再重新分配各动作概率,直至完成规划。将被选动作乘系数180/π后与被控量θ∈(θ1,θ2)求和,达到使被控连杆角度发生偏移的目的。

2.3 定量评价单元

定量评价单元用来评价学习策略的优劣,笔者提出的定量评价策略遵循的原则是：求取当前位置和目标点gend(x,y)间的欧氏距离‖d(k)‖,若变大,则说明学习过程恶化,惩罚此次行为； 反之,奖励该动作。

根据上述原则,传统方法通常以‖d(k)‖变化情况确定奖惩量,当‖d(k)‖减小,则给予奖励值1,当‖d(k)‖变大时,则给予惩罚量-1。这易使原本最优动作被次优动作取代,有失评价客观性。因此,笔者提出可根据‖d(k)‖值做出量化评价的函数r(k),表达式如下

(4)

2.4 在线更新机构

学习策略的优劣取决于动作序列累积回报,利用Q值函数对累积回报动态修改,更新步骤如下。

第1步 初始化q1,q2为0。

第2步 搜索动作ak并执行。

第3步 获取对应动作的立即回报r(k)。

第4步 对应图2中的在线更新Q值函数,计算累积回报并更新Q值

(5)

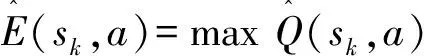
第5步 重复步骤2～4直到达到目标状态为止。

文献[4]证明了在满足一定条件下,式(5)经过迭代后Q函数以概率1收敛。通过在线更新学习经

验,对好的动作给予较高的Q值,使机械臂在以后的学习中可根据Q值状态判断动作的优劣,以此不断优化动作序列。

3 仿真分析

表1 机械臂机械参数表

仿真中随机目标的位置限定在图1所示的扇形区域内,两连杆长度相同。机械参数如表1所示。

利用式(3)的可调ε(k)策略和固定ε(大量实验表明ε=0.24效果最好)策略对同一目标进行30次重复搜索测试,规定最大搜索步数100。比较结果如图3所示。仿真结果说明,可调ε(k)策略前期处于探索阶段,搜索步数较多,随着知识积累和后期的利用,使搜索步数逐渐趋于最少,说明了该策略的有效性。

随机对多目标进行搜索,并调整学习速率,比较相邻参数下的效果。如图4～图6所示,当学习速度由α=0增加到0.6时,稳定性增强； 继续增大速率,稳定性明显降低。说明学习速率影响系统的稳定性。

图3 定值ε和可调ε(k)策略比较 图4 α=0与α=0.3

图5 α=0.3与α=0.6 图6 α=0.7与α=1

表2为不同目标位置时两种策略轨迹规划比较,“*”为末端点轨迹。从表2中看出,改进策略以较少运行步数达到目标位置。表3将规划时间和运行步数作为评价两种策略的指标,可以发现改进策略消耗时间和运行步数更少,进一步验证了改进算法的优越性。

表2 传统策略与改进策略轨迹规划比较

表3 两种策略占CPU时间和运行步数

4 结 语

笔者研究了将一种新的Q学习算法在机械臂轨迹规划上的应用问题。算法中通过改进搜索策略并增设评价单元,同时Q值函数在线修改最优轨迹,最终使机械臂快速达到目标位置。较之传统方法不仅克服局部最优解问题,同时也增强了系统的稳定性和快速性。仿真结果表明了该算法的有效性,可扩展应用于更高自由度的机械臂控制中。

参考文献：

[1]党进,倪风雷,刘业超,等.基于新型补偿控制策略的柔性关节控制器设计[J].机器人,2011,33(2):150-155.

DANG Jin,NI Feng-lei,LIU Ye-chao,et al.Design for Flexible Joint Controller Based on a New Compensation Control Strategy[J].Robot,2011,33(2):150-155.

[2]YU Zhi-gang,SHEN Yong-quan,SONG Zhong-min.Robust Adaptive Motion Control for Manipulator[J].Control Theory &Applications,2011,28(7):1021-1024.

[3]DUGULEANA M,BARBUCEANU F G.Obstacle Avoidance of Redundant Manipulators Using Neural Networks Based Reinforcement Learning[J].Robotics and Computer-Integrated Manufacturing,2012,28(2):132-146.

[4]YE Jian,QIAO Jun-fei,LI Ming-ai,et al.A Behavior-Based Intelligent Controller for a 2-Dof Manipulator[J].Control Theory &Applications,2007,24(3):441-448.

[5]SARMADI,HENGAMEH.Q-Learning Applied to Genetic Algorithm-Fuzzy Approach for On-Line Control in Autonomous Agents[J].Journal of Intelligent Systems,2009,18(1/2):1-31.

[6]CHEN K,KE W D,PENG Z P.An Improved Cooperative Method of Q Learning on Soccer Robot[J].Journal of Harbin Institute of Technology:New Series,2011,18(1):38-40.

[7]KHRIJI L,TOUATI F,BENHMED K,et al.Mobile Robot Navigation Based on Q-Learning Technique[J].International Journal of Advanced Robotic Systems,2011,8(1):45-51.

[8]吴洪岩,刘淑华,张嵛.基于RBFNN的强化学习在机器人导航中的应用[J].吉林大学学报:信息科学版,2009,27(2):185-190.

WU Hong-yan,LIU Shu-hua,ZHANG Yu.Application of Reinforcement Learning Based on Radial Basis Function Neural Networks in Robot Navigation[J].Journal of Jilin University:Information Science Edition,2009,27(2):185-190.

[9]GOMES E R,KOWALCZYK R.Dynamic Analysis of Multi-Agent Q-learning withε-Greedy Exploration[C]∥Proceedings of the 26th International Conference on Machine Learning.New York,NY,USA:ACM,2009:369-376.

[10]AKRAMIZADEH A,AFSHAR A,MENHAJ M B.Exploration Strategies inn-Person General-Sum Multiagent Reinforcement Learning with Sequential Action Selection[J].Intelligent Data Analysis,2011,15(6):913-929.