一类三元ZCZ序列偶集的构造法

许成谦,路江海

(燕山大学 信息科学与工程学院,河北 秦皇岛 066004)

0 引 言

近年来,准同步码分多址(AS-CDMA：Approximately Synchronized-Code Division Multiply Access)引起了人们的广泛关注。在AS-CDMA通信系统中,同步误差控制在一定的范围内(一个或几个码片周期),相应地要求扩频序列在同步误差范围内具有或接近理想相关特性,以减小甚至消除共道干扰和多径干扰[1]。针对上述情况,文献[2,3]给出了零相关区的概念,构造很多能满足要求的ZCZ(Zero Correlation Zone)序列集。序列偶理论的提出进一步拓宽了扩频序列的存在空间[4]。序列偶的理论改变了传统相关检测的做法,把序列偶中的一个序列作为发射端的扩频序列,而另一个序列作为接收端的扩频序列。文献[5]利用迭代法、级联法和递归构造出二元ZCZ序列偶,给出ZCZ序列偶存在的必要条件和理论界。刘凯等[6]提出利用差集偶构造二元ZCZ序列偶集。文献[7,8]将屏蔽序列偶应用于低/零相关区中,构造出屏蔽低/零相关区序列偶集,把伪随机序列应用到ZCZ序列偶中,提出了三元的ZCZ序列偶集的构造方法[9]。文献[10]把序列偶集的构造扩展到了多相。后来一些学者用递归[11]、移位和用酉矩阵扩展[12]等方法构造了大容量的ZCZ序列偶集。把序列偶的理论应用到阵列偶中[13,14],构造出ZCZ阵列偶集。笔者给出了新的序列偶集合的构造方法,得出的ZCZ序列偶集,通过减小零相关区长度即可增大序列偶的数量,从而增加用户的数量。

1 基本概念

定义1 设a=(a0,a1,…,aN-1)和b=(b0,b1,…,bN-1)是两个长度为N的序列,a,b组成一个序列偶,记为(a,b),如果序列偶(a,b)自相关函数满足

(1)

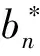
定义2 设(a,b),(c,d)是周期长度为N的序列组成的序列偶,则序列偶(a,b)和(c,d)的周期互相关函数定义为

(2)

定义3T是含有M个序列偶的集合,T={(a0,b0),(a1,b1),…,(aM-1,bM-1)},集合中组成序列偶的序列周期为N,如果任意两个序列偶的周期相关函数满足关系式

(3)

则集合T是一个(N,M,Z)-ZCZ序列偶集。其中N是集合中构成序列偶的序列长度,M是集合中序列偶的个数,Z是零相关区长度。定义序列偶集的渐进率

(4)

由ZCZ序列偶集的理论界[6]可知,η≤1,当η=1时称ZCZ序列偶集是达到理论界限的最佳序列偶集。

定义4 设A,B为M×N阶矩阵,如果ABT=cIM,则称(A,B)为正交矩阵偶[15],其中BT为B的转置矩阵。

定义5 设a=(a0,a1,…,aN-1)为长度为N的序列,u=(u0,u1,…,um-1)为长度为m的向量,N=km。定义序列a与向量u的运算及序列偶(a,b)与向量u的运算如下

a⊕u=(a0u0,a1u1,…,am-1um-1,amu0,…a2m-1um-1,…,aN-1um-1)

(5)

(a,b)⊕u=(a⊕u,b⊕u)

(6)

定义6 设a=(a0,a1,…,aN-1)为长度为N的序列,序列a左移位运算定义如下

Lτ(a)=(aτ,aτ+1,…,aN-1,a0,a1,…,aτ)

(7)

L为左移位算子。

定义7 设a=(a0,a1,…,aN-1)为长度为N的序列,X是一个n0×n1阶矩阵

并且满足gcd(N,n1)=1,假设N>n1,序列a和矩阵X运算得到

Y=Xoa=[y0,y1,…,yn0-1]T

(8)

YT表示矩阵[y0,y1,…,yn0-1]的转置矩阵,矩阵Y中每个元素是长度为Nnr的序列,具体如下

(9)

定义8 设U={u0,u1,…,uk-1}是含有k个向量的集合,对于0≤g≠h

2 ZCZ序列偶集的构造

笔者给出一种新的序列偶集合的构造方法,该方法基于三元最佳序列偶和正交矩阵偶(二元或三元),具体的构造步骤如下。

第1步 取一个三元最佳序列偶(a,b),序列偶中序列的长度为n0,再取一个n1×n2阶正交矩阵偶(H,R),并且满足gcd(n0,n2)=1,假设n0>n2。序列偶(a,b)中的序列a,b表示为a=(a0,a1,…,aN-1),b=(b0,b1,…,bN-1)。正交矩阵偶(H,R)的矩阵表示为

序列a与矩阵H按照定义7的运算得到C=Hoa,序列b与矩阵R运算得到D=Rob,具体如下

C=[c0,c1,…cn1-1]T

(10)

D=[d0,d1,…dn1-1]T

(11)

其中ci表示矩阵C的第i行,di表示矩阵D的第i行,分别表示为

(12)

(13)

其中ci,di为长度为n0n2的序列,(ci,di)组成一个序列偶,序列偶中的序列长度为n0n2。所有行组成一个含有n1序列偶的序列偶集E={(c0,d0),(c1,d1),…,(cn1-1,dn1-1)},0≤i

第2步 对已构造的n1个序列偶的序列按定义6进行移位,得到新的序列偶集合

S={s0,0,s0,1…,s0,k-1,s1,0,s1,1,s1,k-1…,sn1-1,0,sn1-1,1,…,sn1-1,k-1}

(14)

si,t=(Ltαci,Ltαdi) 0≤i

(15)

在这里补充一个条件：kα

第3步 取向量集合U={u0,u1,…,uk-1},集合中向量的长度为n2,并且集合中的向量满足移位不等价条件。按照定义5序列偶(Ltαci,Ltαdi)和ut运算,得到新的序列偶集合

P={p0,0,p0,1,…,p0,k-1,p1,0,p1,1,…,p1,k-1,…,pn1-1,0,pn1-1,1,…,pn1-1,k-1}

(16)

pi,t=(Ltαci⊕ut,Ltαdi⊕ut) 0≤i

(17)

定理1 通过第1步得到的序列偶集E是一个(n0n2,n1,n0-1)-ZCZ序列偶集。

证明 设(ci,di),(cj,dj)是集合E中任意两个ZCZ序列偶(0≤i

根据矩阵H和R的正交性和(a,b)是最佳序列偶可得

(18)

所以定理1成立。

定理2 通过上述3个构造步骤得到的P是一个含有kn1个序列偶的集合,序列偶中序列的长度为n0n2,kn1个序列偶组成一个(n0n2,kn1,α)-ZCZ序列偶集。

证明 设pi,t,pj,g是集合P中任意两个序列偶,这两个序列偶的周期相关函数如下

Rpi,t,pj,g(τ)=RLtαci⊕ut,Lgαdj⊕ug(τ)=(Ltαci⊕ut)(Lτ((Lgαdj)⊕(ug)))=

(Ltαci⊕ut)(Lτ(Lgαdj)⊕Lτ(ug))=(Ltαa)(Lgα+τb)(Ltαhi⊕ut)(Lτ((Lgαrj)⊕ug))=

R(a,b)((g-t)α+τ)RLtαhi⊕ut,(Lgαrj)⊕ug(τ)

根据矩阵H和R的正交性和(a,b)是最佳序列偶,可得

(19)

当i≠j,τ=0时,因为hi和rj相互正交,又因为t=g,所以

RLtαhi⊕ut,(Lgαrj)⊕ug(τ)=0

定理2成立。

推论 如果将最佳序列偶(a,b)替换为(N1,M1,Z1)-ZCZ序列偶集,在这里gcd(n0,N1)=1,kα

证明推论的过程和证明定理2的过程类似,和定理2不同的是要对序列ai,bj是否属于同一个序列偶进行讨论,定理2是推论的一种情况,即ai,bj是同一个序列偶里的两个序列。

构造实例 周期为5的三元最佳序列偶(a,b)=(++000,++-+-),取k=2,α=1,正交矩阵偶

U={(++),(--)},“+”表示1,“-”表示-1,按照定理2可以构造出1个ZCZ-(10,4,1)序列偶集,具体如下

3 性能分析

根据定义3得到的ZCZ序列偶集P是一个(n0n2,kn1,α)-ZCZ序列偶集,其渐进率为

(20)

序列偶集合中的序列偶的个数和零相关长度随参数的变化而变化。如果取k=1,n1=n2,α=n0-1,则η=1,所以,构造的ZCZ序列偶集的性能参数达到了理论界。从最终的构造结果看,改变k和α的值,即可得出不同的ZCZ序列偶集。通过减小α,可增大k的值,从而可增加序列偶的数量。在实际的应用中,序列偶数目直接决定了系统可支持用户的多少,因而序列集中序列偶数目越多越好,以减小序列偶的零相关区长度为代价,换取更多的ZCZ序列偶数量的方法是可行的方法。

4 结 语

笔者给出一种新的构造ZCZ序列偶集方法。该方法基于三元最佳序列偶和正交矩阵偶,构造的ZCZ序列偶集的序列偶的数目和零相关区长度的乘积满足一定的条件,而且随着设定参数的改变而改变,通过改变设定的参数值即可得到不同的ZCZ序列偶集,通过该构造方法得出的ZCZ序列偶集适用于多种延时的准同步CDMA通信系统。

参考文献：

[1] FAN P Z,HAO L.Generalized Orthogonal Sequences and their Applications in Synchronous CDMA Systems[J].IEICE Trans Fundamentals,2000,E83-A(11):2054-2069.

[2]FAN P Z,SUEHIRO N,KUROYANAGI.A Class of Binary Sequence with Zero Correlation Zone[J].Electronics Letters,1999,35(10):777-779.

[3]LONG B Q,ZHANG P,HU J D.A Generalized QS-CDMA System and the Design of New Spreading Codes[J].IEEE Transactions Vehicular Technology,1998,47(4):1268-1275.

[4]赵晓群,何文才,王仲文.最佳二进阵列偶理论研究[J].电子学报,1999,27(1):34-37.

ZHAO Xiao-qun,HE Wen-cai,WANG Zhong-wen.The Theory of the Binary Array Pairs[J].Journal of Electronic,1999,27(1):34-37.

[5]梁清梅,刘金明,许成谦.一种达到理论上限的新型扩频序列集[J].无线电工程,2006,30(10):27-30.

LIANG Qing-mei,LIU Jin-ming,XU Cheng-qian.A Novel Spread Spectrum Sequence Set up to Upper Bound of Theory[J].Radio Engineering of China,2006,30(10):27-30.

[6]刘凯,许成谦,刘洺辛.由平方剩余差集与差集偶构造二元ZCZ序列偶集[J].北京邮电大学学报,2009,32(4)：50-53.

LIU Kai,XU Cheng-qian,LIU Ming-xin.Construction of Binary ZCZ Sequence Pair Based on Quadratic Difference Set and Difference Set Pair[J].Journal of Beijing University of Post and Telecommunications,2009,32(4):50-53.

[7]许蕾,蒋挺,周正.最佳屏蔽二进序列偶在低/零相关区中的应用研究[J].通信学报,2006,27(10)：19-24.

XU Lei,JIANG Ting,ZHOU Zheng.Application Research of Perfect Punctured Binary Sequence Pair in LCZ/ZCZ[J].Journal of Communication,2006,27(10):19-24.

[8]李兆斌,魏占祯,池亚平.ZCZ屏蔽序列偶集的构造方法[J].北京邮电大学学报,2011,34(3):17-20.

LI Zhao-bin,WEI Zhan-zhen,CHI Ya-ping.Construction Method of ZCZ Puncture Sequence Pair Set[J].Journal of Beijing University of Post and Telecommunications,2011,34(3):17-20.

[9]李兆斌,蒋挺,周正.基于伪随机序列的零相关区三元序列偶集的研究[J].通信学报,2009,30(8)：27-31.

LI Zhao-bin,JIANG Ting,ZHOU Zheng.Study on ZCZ Ternary Sequence Pair Based on Pseudo Random Sequence[J].Journal of Communication,2009,30(8):27-31.

[10]肖丽萍,许成谦.最佳几乎四相信号[J].吉林大学学报：工学版,2011,41(3):855-858.

XIAO Li-ping,XU Cheng-qian.Perfect Almost-Quadphase Signal[J].Journal of Jilin University：Engineering and Technology Edition,2011,41(3):855-858.

[11]王志华,柯品惠,张胜元.ZCZ序列偶集的构造研究[J].福建师范大学学报:自然科学版,2010,26(5):16-19.

WANG Zhi-hua,KE Pin-hui,ZHANG Sheng-yuan.Study on the Construction of ZCZ Sequence Pair Set[J].Journal of Fujian Normal University:Natural Science Edition,2010,26(5):16-19.

[12]肖丽萍,李卫卫,许成谦.ZCZ序列偶集及大容量ZCZ序列偶集的构造[J].北京邮电大学学报,2010,33(5):89-93.

XIAO Li-ping,LI Wei-wei,XU Cheng-qian.Construction of ZCZ Sequence Pairs Set and ZCZ Sequence Pairs Set with Large Family Size[J].Journal of Beijing University of Post and Telecommunications,2010,33(5):89-93.

[13]柯品惠,王志华,张胜元.基于交织方法的ZCZ阵列偶集的构造研究[J].电子与信息学报,2010,33(5):89-93.

KE Pin-hui,WANG Zhi-hua,ZHANG Sheng-yuan.Construction of ZCZ Array Pairs Set by Interleaving Techniques[J].Journal of Electronic and Information,2010,33(5):89-93.

[14]高军萍,李琦,戴居丰,等.ZCZ阵列偶及构造方法研究[J].通信学报,2008,29(9):62-67.

GAO Jun-ping,LI Qi,DAI Ju-feng,et al.Research of ZCZ Array Aair and Its Construction Method[J].Journal of Communication,2008,29(9):62-67.

[15]刘凯,许成谦,李刚.二元二值周期自相关序列偶的应用研究[J].电子信息学报,2009,31(7):1536-1541.

LIU Kai,XU Cheng-qian,LI Gang.Application Research on Binary Sequence Pairs with Two-Level Periodic Autocorrelation[J].Journal of Electronic and Information,2009,31(7):1536-1541.