时滞三角型混沌系统的滑模自适应同步控制方法

梅 蓉

(南京森林警察学院 侦查系,南京 210046)

0 引 言

三角型混沌系统是非线性系统中结构最简单的一种系统,在客观世界中也是普遍存在的,因此,研究三角型混沌系统及其应用具有重要意义。到目前为止,三角型混沌系统的同步控制问题得到了广泛的研究[1-3]。文献[1]主要基于Lyapunov方法和backstepping方法实现四维三角型系统的同步;文献[2]主要基于Lyapunov方法和backstepping方法实现参数未知Genesio三角型混沌系统的同步;而文献[3]也利用Lyapunov方法和backstepping方法实现参数未知混沌系统的自适应同步。但在现有的研究成果中,很少考虑到三角型混沌系统的结构不确定性,笔者将采用滑模自适应控制方法设计时滞不确定三角型混沌系统的同步控制问题。

对于参数确定或不确定的混沌系统,要实现同结构或异结构混沌系统的同步,自适应同步控制[4-7]、滑模控制[8,9]、滑模自适应同步控制[10-12]、线性同步控制[13]和主动同步控制[14,15]等都是常用的控制方法,但文献[4-15]所设计的控制器都是多维控制器。为了便于实际应用,笔者运用自适应滑模控制设计单维同步控制器实现具有参数不确定性的三角型混沌系统同步,有效地减少了同步控制器的维数。将该同步控制方法实现混沌同步保密通信,单维的同步控制器在同步电路实现时也更为简单容易,因此,笔者设计的单维同步控制器具有较为重要的实际意义。

1 时滞三角型混沌系统的构建和混沌判定

在工程中有许多实际系统具有三角型结构,同时也可以通过反馈线性化的方法将非三角型系统转化为三角型系统。因而,研究三角型混沌系统具有重要的实际意义。

1.1 时滞三角型混沌系统的构建

常见的三角型混沌系统形式如下

(1)

其中x=[x1,x2,…,xn]T∈Rn为系统状态向量,f(x,t)∈R,g(x)∈R均为非线性项,φ∈R为未知常数或时变常数,w为系统不确定项。

通过引入时滞非线性项,构建如下三维时滞三角型系统

(2)

其中k为时滞非线性项参数,τ为延迟时间。

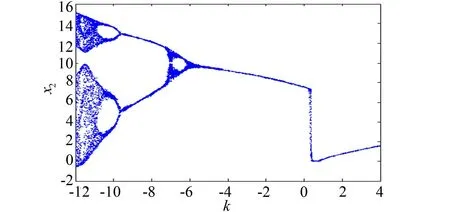
图1 系统(2)参数k变化的状态x2的分岔图

利用系统分岔图分析各个参数变化时系统(2)部分状态的变化情况。系统初始状态条件为x(t)=[0.1,0.1,0.2]T,-τ≤t≤0,选取τ=0.35,分析随着参数k变化系统(2)动力学变化特性。图1为k∈[-12,4]的时滞三角型系统(2)的分岔图。k=-11,随着τ的取值不同,系统也表现出不同的动力特性(见图2)。

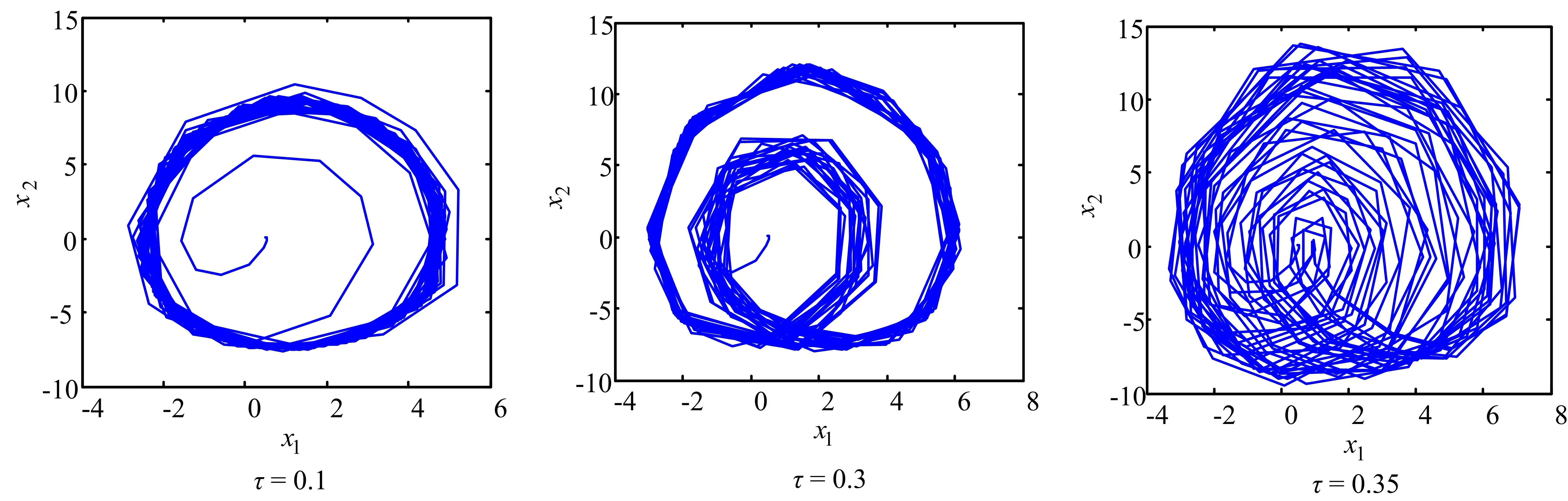
图2 τ取不同值时的时滞三角型系统(2)的x1-x2相图

由图1和图2可看出,时滞三角型系统(2)的动力学特性敏感依赖于参数k,τ。图1是状态变量x2关于参数k的分岔图,参数k的取值范围[-12,4]。从图1中可看出,当参数k从-12开始,以步进长0.01变化到4,状态变量x2从混沌运动形成周期运动、混沌运动、周期运动、混沌运动、周期运动的交替过程。图2是状态变量x1-x2的相图,τ=0.1为倍周期运动,τ=0.3,0.35为混沌运动,实验仿真发现,τ>0.35时系统发散。由图2可看出,随着τ的变化,系统的动力学特性发生很大的变化。

1.2 时滞三角型系统的混沌判定

在系统初始状态x(t)=[0.1,0.1,0.2]T条件下,取τ=0.35,k=-6.5。经数值仿真可得时滞三角型系统(2)的状态空间图、相图、功率谱图、Poincare映射图,分别如图3～图6所示。由图3和图4可知系统运动轨迹局限在一定的区域内,且永不重复地运动;图5显示状态x1的功率谱出现了连续功率谱叠加尖峰;图6表示的是Poincare映射图。由该图可看出,Poincare映射图包含不同方向的分支,且有成片的密集点;参数k=-6.5时,最大Lyapunov指数Lmax=7.460 5,这些特征均可确定系统(2)表现出混沌行为。

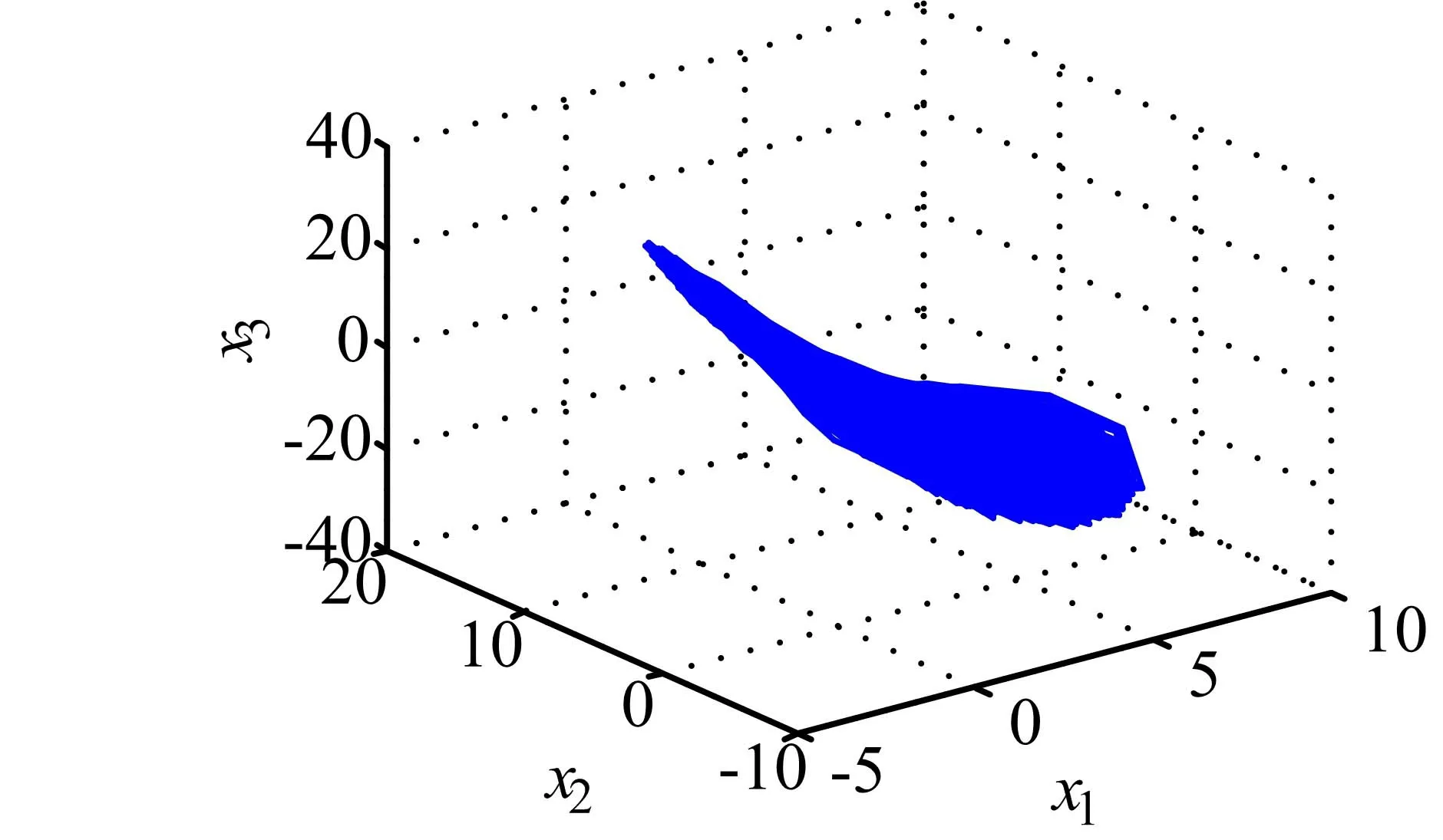
图3 系统(2)的x1-x2-x3空间图

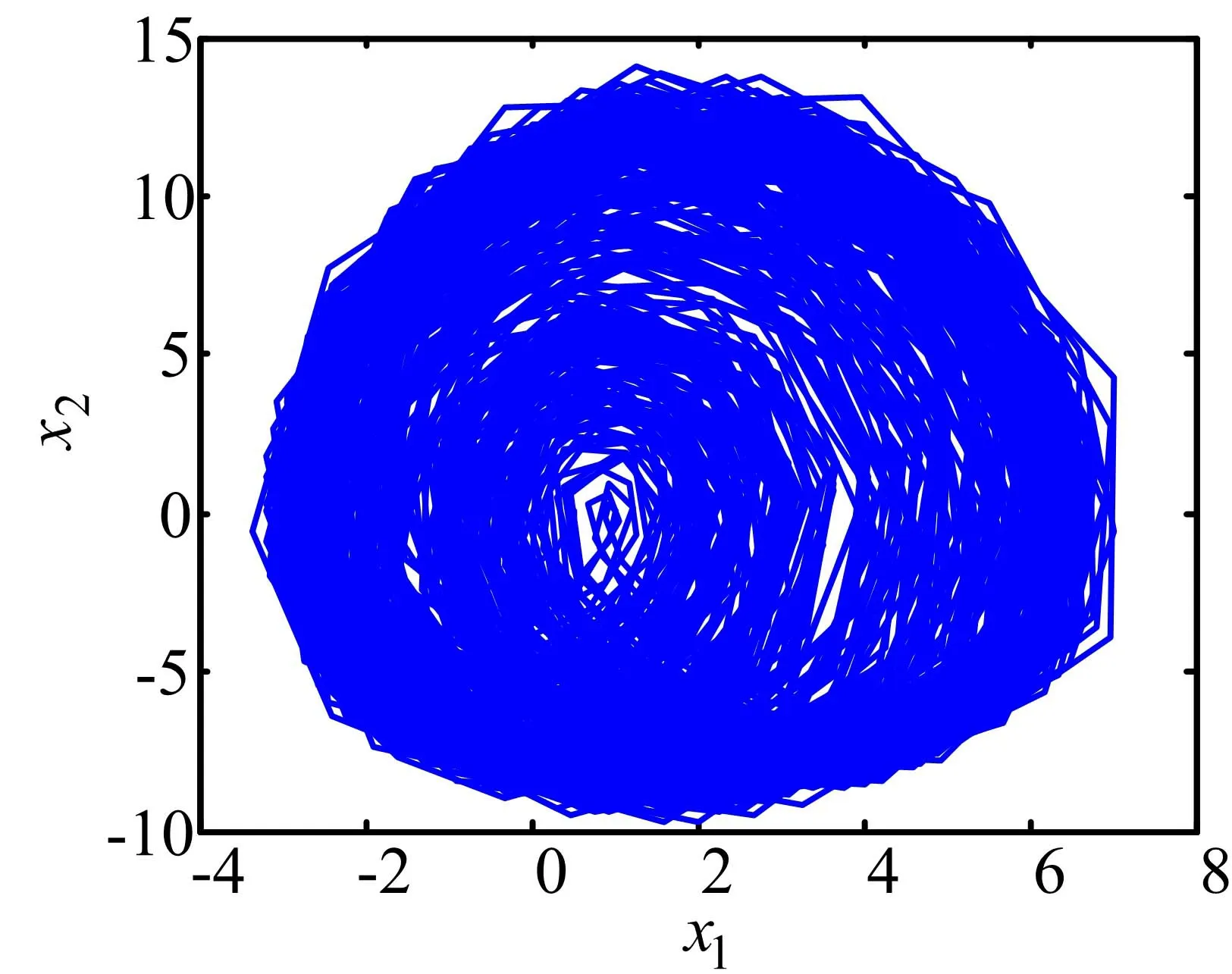
图4 系统(2)的x1-x2相图

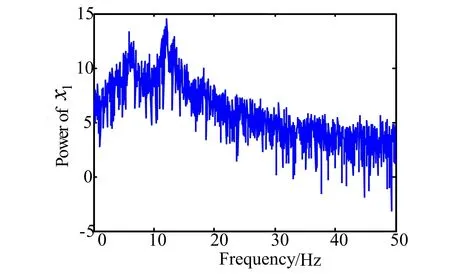
图5 系统(2)的状态x1功率谱

图6 系统(2)的Poincare映射

2 三角型不确定混沌系统滑模自适应同步控制器的设计

根据三角型混沌系统(2),给出如下时滞不确定三角型混沌系统

(3)

其中x=[x1,x2,x3]T∈R3为时滞不确定三角形混沌系统的状态向量,θi(t)∈Rm×1(1≤i≤3)为系统未知参数,τ为混沌系统的时间延迟。

考虑将系统(3)作为主系统,对应的从系统为

(4)

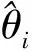
(5)

滑模面设计为

s=e3+c1e1+c2e2

(6)

其中c1和c2为大于零的设计参数。

定理 对于混沌同步误差系统(5),如果选取系统参数自适应变化律为

(7)

则单维同步控制输入可设计为

(8)

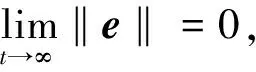
证明 选择如下的Lyapunov函数

(9)

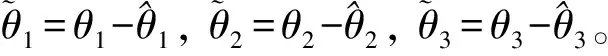
对式(9)两边求导可得

(10)

将式(5)和式(6)代入式(10)有

将单维同步控制输入式(8)代入式(11)有

(12)

将式(7)代入式(12)可得

(13)

由式(13)可得

(14)

式(14)也可写成

(15)

则得到s∈L2,根据Barbalat引理可知,当t→∞,s→ 0,则由式(6)可推出t→∞,e→ 0。

由式(15)可知,混沌误差系统是稳定的,即在单维控制输入式(8)作用下系统(4)和系统(3)达到同步,证明完毕。

3 数值仿真

为验证所提出的滑模自适应同步控制方法的有效性和科学性,在Matlab 7.0工作环境下进行数值仿真。主系统(3)的初始值为[0.3,0.1,0.3]T,从系统(4)的初始值为[1,3,2]T,选取时变未知参数θ1(t)=e-0.5t,θ2(t)=e-t,θ3(t)=9e-2t,τ=0.35,该系统的状态相图和空间图如图7所示。

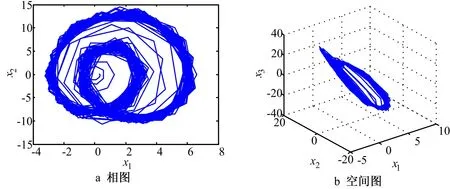
图7 三角型混沌系统(3)状态相图和空间图

由图7可看出,尽管存在不确定项,系统仍然保持混沌特性。为使混沌系统(3)和(4)达到同步,按式(8)设计单维同步控制器,其中滑模面选取为

s=e3+2e1+2e2

系统参数自适应变化律为

取控制器设计参数r=10,则控制器设计为如下形式

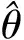
图8 系统(3)和(4)的同步误差

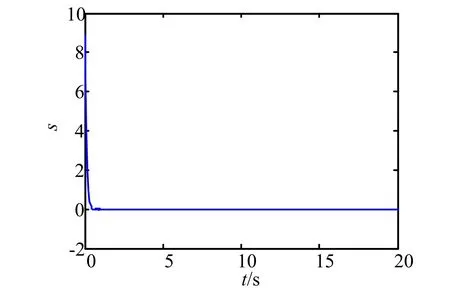
图9 滑模面

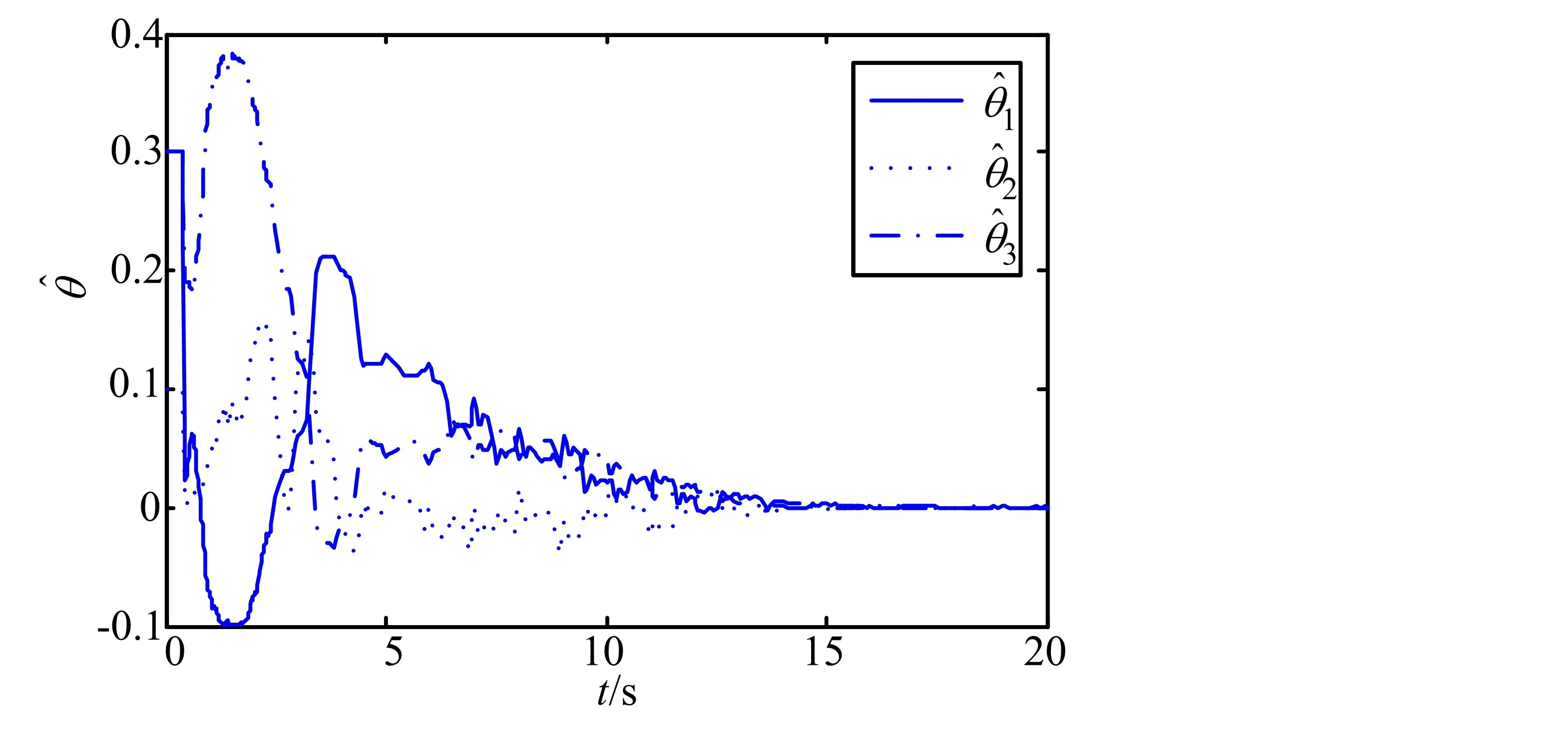
图10 系统参数自适应变化律

图11 控制输入u(t)

4 结 语

笔者研究了不确定时滞三角型混沌系统同步控制器的设计。设计了一类时滞三角型系统,通过分岔图分析了随着参数的变化系统的动力学特性发生变化的情况;利用Poincare映射、功率谱分析、最大Lyapunov指数等判定时滞三角型系统是否为混沌系统;利用滑模控制和自适应控制方法设计了单维同步控制器。实验仿真表明,设计的不确定时滞三角型混沌系统同步控制器的有效性。

参考文献:

[1]WANG Bo,WEN Guang-jun.On the Synchronization of a Class of Chaotic Systems Based on Backstepping Method[J].Physics Letters A,2007,370(1):35-39.

[2]JU H PARK.Synchronization of Genesio Chaotic System via Backstepping Approach[J].Chaos,Solitons and Fractals,2006,27(5):1369-1375.

[3]YU Yong-guang,ZHANG Suo-chun.Adaptive Backstepping Synchronization of Uncertain Chaotic System[J].Chaos,Solitons and Fractals,2004,21(3):643-649.

[4]ZHANG Gang,LIU Zeng-rong,ZHANG Jian-bao.Adaptive Synchronization of a Class of Continuous Chaotic Systems with Uncertain Parameters[J].Physics Letters A,2008,372(4):447-450.

[5]WANG Yan-wu,WEN Chang-yun,YANG Meng,et al.Adaptive Control and Synchronization for Chaotic Systems with Parametric Uncertainties[J].Physics Letters A,2008,372(14):2409-2414.

[6]SUN Yong-hui,CAO Jin-de.Adaptive Synchronization Between Two Different Noise-Perturbed Chaotic Systems with Fully Unknown Parameters[J].Physica A:Statistical Mechanics and Its Applications,2007,376(15):253-265.

[7]GE Zheng-ming,YANG CHENG-HSIUNG.Pragmatical Generalized Synchronization of Chaotic Systems with Uncertain Parameters by Adaptive Control[J].Physica D:Nonlinear Phenomena,2007,231(2):87-94.

[8]HER-TERNG YAU.Chaos Synchronization of Two Uncertain Chaotic Nonlinear Gyros Using Fuzzy Sliding Mode Control[J].Mechanical Systems and Signal Processing,2008,22(2):408-418.

[9]余洋,米增强,刘兴杰.双馈风力发电机混沌运动分析及滑模控制混沌同步[J].物理学报,2011,60(7):112-119.

YU Yang,MI Zeng-qiang,LIU Xing-jie.Analysis of Chaos in Doubly Fed Induction Generator and Sliding Mode Control of Chaos Synchronization[J].Acta Physica Sinica,2011,60(7):112-119.

[10]TSUNG-CHIH LIN,CHEN Ming-che,MEHDI ROOPAEI.Synchronization of Uncertain Chaotic Systems Based on Adaptive Type-2 Fuzzy Sliding Mode Control[J].Engineering Applications of Artificial Intelligence,2011,24(1):39-49.

[11]MEHDI ROOPAEI,MANSOOR ZOLGHADRI JAHROMI,ROBERT JOHN,et al.Unknown Nonlinear Chaotic Gyros Synchronization Using Adaptive Fuzzy Sliding Mode Control with Unknown Dead-Zone Input[J].Communications in Nonlinear Science and Numerical Simulation,2010,15(9):2536-2545.

[12]MOHAMMAD POURMAHMOOD,SOHRAB KHANMOHAMMADI,GHASSEM ALIZADEH.Synchronization of Two Different Uncertain Chaotic Systems with Unknown Parameters Using a Robust Adaptive Sliding Mode Controller[J].Communications in Nonlinear Science and Numerical Simulation,2010,16(7):2853-2868.

[13]姜玉秋.Lorenz混沌系统的线性同步控制[J].吉林大学学报:信息科学版,2011,29(6):571-575.

JIANG Yu-qiu.Linear Synchronization for Lorenz Chaotic System[J].Journal of Jilin University:Information Science Edition,2011,29(6):571-575.

[14]张袅娜,周邃,张德江.基于主动控制的异结构混沌系统有限时间同步[J].吉林大学学报:工学版,2011,41(4):1131-1134.

ZHANG Niao-na,ZHOU Sui,ZHANG De-jiang.Synchronization Control of Finite Time Convergence between Two Different Structure Chaos Systems[J].Journal of Jilin University:Engineering and Technology Edition,2011,41(4):1131-1134.

[15]王兴元,朱全龙,张晓鹏.基于三种方法的新Lü混沌系统的同步[J].物理学报,2011,60(10):1-10.

WANG Xing-yuan,ZHU Quan-long,ZHANG Xiao-peng.Synchronization of New Lü Chaotic System via Three Methods[J].Acta Physica Sinica,2011,60(10):1-10.