双馈风力发电机交流励磁及其幅度频率控制

廖恩荣，唐志伟

（1.南京高精传动设备集团有限公司，江苏南京211151;2.嘉兴电力局，浙江嘉兴 314000）

0 引言

风力发电在国内外发展迅速［1］。变速恒频双馈（doubly fed induction generator DFIG）风力发电是风力发电的主流类型之一，与传统的同步发电机直流励磁不同，DFIG实行交流励磁，可调量有三个:励磁电流幅值、励磁电流频率、励磁电流相位。通过改变励磁电流频率，双馈电机可以调节转速，从而实现变速恒频运行;通过调节励磁电流的幅值和相位，可达到调节有功功率和无功功率的目的。与同步发电机相比，控制量多了两个，控制上更加灵活，但控制也更加复杂［2-4］。

双馈发电机的控制策略取得了很多成果，应用最广的控制策略是矢量控制策略（vector control）［5］，矢量控制实现了电动机有功和无功功率的解耦控制，动态性能好，但控制策略比较复杂且需要精确的定子磁链和转子位置角。直接功率控制（direct power control）［6-7］利用直接转矩控制的思路，将电力电子变流器和电机合并，通过开关矢量直接控制电机的有功和无功功率，简化了控制策略的设计，但由于其开关频率不固定增加了滤波器设计的难度。转子磁链幅值和角度控制（flux magnitude and angle control）［8-12］通过转子磁链的角度和幅值来控制定子的有功和无功功率，但控制复杂。

通过对电压电流等易测量的磁链观测估计转速和转子位置信号的无速度传感器方法［13-14］，一方面增加了控制系统的复杂性，另一方面其估计精度受参数变化、运行状态的影响。

本文从双馈电机的原理出发，简要叙述了电网侧和转子侧变频器矢量控制策略;为了避免转子位置编码器的影响，提出了无需测量转子位置信号的幅度频率控制策略;仿真验证了幅度频率控制策略的有效性，提高了系统的可靠性。

1 双馈风力发电机原理

图1 不同风速下风力机的输出机械功率特性曲线

对于一台确定的风力机，在风速和桨叶节距角一定时，总存在一个最佳叶尖速比对应着一个最大的风能转换系数，此时风力机的能量转换效率最高。图1为不同风速下风力机的输出机械功率特性曲线，从图1中看出，对于一个特定的风速，风力机只有运行在一个特定的机械角速度下，风力机才会获得最大的能量转换效率［15］。因此，变速风电机组才能捕获最大风能，提高发电效率。

双馈风力发电机组的结构示意图如图2所示，DFIG的转子经变流器与电网相连，利用交流转子励磁和DFIG配合实现变速恒频。

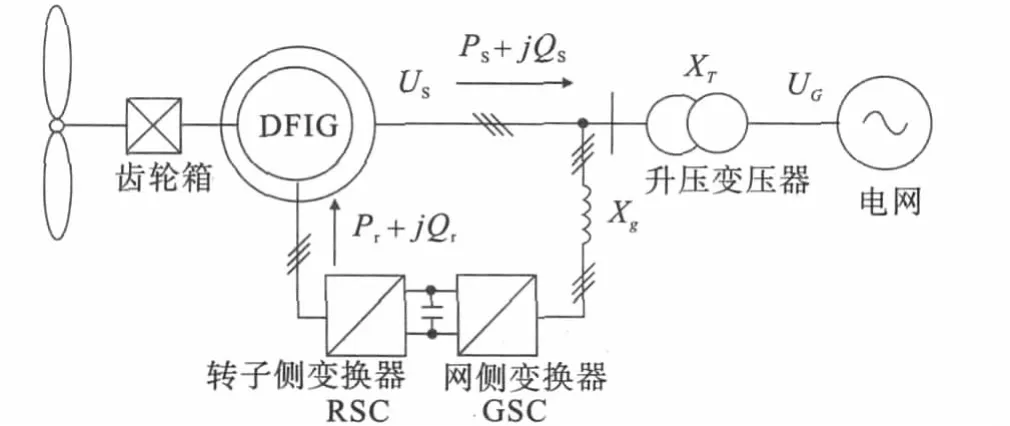
图2 双馈风力发电机结构示意图

变速恒频原理如式（1）所示:

式（1）中，fm，fr，fs分别代表转子转速、转子电流和定子电流的频率，Np表示双馈电机的极对数。当双馈风机发电机运行时，风力机带动转子以fm的频率旋转，形成电角频率为Npfm的旋转磁场，由于转子励磁电流矢量的频率为fr，气隙中感应出与定子电流同频率的合成磁场，频率由式（1）表示。因此双馈电机实现了变速恒频［16］。

将转子侧的各个物理量折合到定子侧，通过Park变换将abc坐标系下的异步电机方程变换到一般的dq旋转坐标系可以推导出双馈电机的电压和磁链方程分别如式（2）和式（3）所示（定子侧按发电机惯例，转子侧按电动机惯例）［16］。

转矩方程可以表示成:

转子运动方程可以表示成:

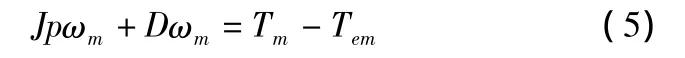
式（2）到式（6）中，uds，uqs为定子电压的d，q轴分量，ud r，uq r为转子电压的d，q轴分量，Ids，Iqs为定子电流的d，q轴分量，Id r，Iq r为转子电流的d，q轴分量，ψds，ψqs为定子磁链的d，q轴分量，ψd r，ψq r为转子磁链的d，q轴分量，rs，rr，Ls，Lr为定、转子的电阻、电感，Lm为互感，ωs，ωr，ωm为定子磁链、转子电流、转子旋转的角速度，Tm，Tem为机械转矩、电磁转矩，P为微分算子，J，D为转动惯量、摩擦系数。取ωs等于定子旋转磁场的角速度，这样dq坐标系就变成了同步旋转坐标系，ABC坐标系下的正弦量对应于dq坐标系下的直流量。

2 双馈电机电网侧变流器控制

网侧变流器是一个电压源型PWM整流器，控制变流器直流母线电压，且功率因数可调，实现功率的双向流动。其矢量控制框图如图3所示［4］。

图3 网侧变流器矢量控制策略框图

图3中，id g，iq g为网侧变流器电流的d，q轴分量，Lg为网侧变流器电感，udc为网侧变流器直流电压，us为网侧变流器交流电压d轴分量，ωs为网侧变流器交流电压频率，Qg为电网侧变流器的无功功率，θs为电网电压位置角。dq轴电压通过dq→ABC变换之后得到PWM整流器输出的三相电压。

3 双馈电机转子侧变流器控制

双馈电机并网时，转子侧变流器控制目标为控制定子的有功和无功功率，双馈电机定子的有功功率Ps和无功功率Qs可以表示成:

按照定子磁链定向的方式，忽略定子磁链的暂态和定子电阻，将d轴固定在定子磁链矢量的轴线ψs上，于是ψds=ψs，ψqs=0，代入式（2）的前两式可以得到:

将式（7）代入式（6）可以得到

再将磁链定向结果代入式（3）可以得到

将式（9）代入式（8）可以得到:

从式（10）可以看出，如果定子磁链和频率保持不变，按照定子磁链定向之后，定子的有功功率和转子q轴电流成正比，定子的无功功率和转子d轴电流成正比。

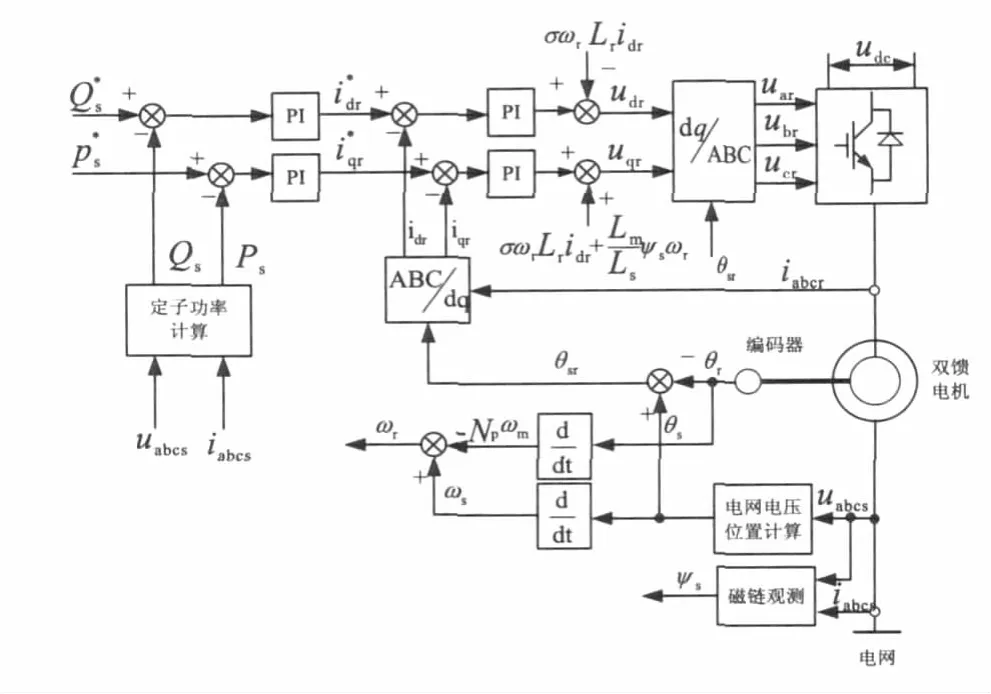
图4 双馈电机并网后矢量控制策略框图

4 同步化双馈电机

4.1 同步化的双馈电机数学模型

虽然双馈电机工作在异步状态下，但是其转子励磁磁场的旋转速度和定子磁场的旋转速度相等，具有和同步电机类似的控制特性［17-18］。双馈电机的功角δ为q轴暂态内电势矢量和定子电压Us之间的夹角，双馈电机的有功和无功表达式可以写成:

式（11）中X`s为定子暂态电抗。可以看出，如果将d轴放在转子合成磁势的轴线上，经过整理后，双馈电机具有和同步电机类似的有功和无功表达式。也就是说，从q轴暂态内电势的角度来看，双馈电机和隐极同步电机等效。

省略定子磁链动态过程的同步化双馈电机三阶方程为式（12）:其中Xs为定子电抗，Edf、Eq f为折合到定子侧的转子dq轴励磁电压，T=表示转子回路的时r0间常数:

此外还有两个定子电压方程和一个附加的转子电压方程:

式（13）中s为转差率，Tr0为 双馈电机在同步点运行时，有约束条件Npωm=ωs，ωr=0。将约束条件代入式（12），同步化双馈电机三阶方程就变成了同步电动机的三阶方程［8，15］。

4.2 双馈电机与同步电机的比较

通过上面的分析可以看到，双馈电机和同步电机有相似的地方也有不同之处，归纳如下:

a）相同点:

1）从q轴暂态内电势的角度来看，双馈电机和隐极同步电机等效;

2）都可以通过励磁控制来调节定子输出的无功功率。

b）不同点:

1）励磁调节:同步电机的励磁电压为直流，只有其幅值可以调节;但双馈电机的励磁电压为交流，有电压幅值、频率和相位三个可调量，控制更加灵活;

2）转速范围:同步电机的转速等于同步转速，但双馈电机既可以超同步运行，也可以次同步运行;

3）转子励磁的功能。同步电机的转子仅提供无功励磁，但双馈电机的转子除提供无功励磁外，还要提供转差有功功率。

5 幅度频率控制策略

矢量控制策略中所需的转子位置信息一般通过增量式或绝对式光电编码器来获得，实际中增量式编码器应用最广，但由于风力发电系统运行的环境比较恶劣，编码器信号很容易受到干扰，这会对系统稳定运行带来负面影响［13-14］。

5.1 幅度频率控制

对式（12）第一项进行分析可以看出，当双馈电机转子电流的角频率ωr≠sωs时，双馈电机的功角δ就会发生变化。从式（11）可以看出，功角的变化可以引起有功和无功功率的变化。

根据同步电机理论，同步电机输出有功功率主要和功角δ有关，输出的无功功率主要和暂态励磁电压E`q的大小有关［8］。根据式（11）可知，这个关系在双馈电机中仍然适用。

当Npωm+ωr＞ωs时，功角增大，有功功率增大;当Npωm+ωr＜ωs时，功角减小，有功功率减小。由于转子侧采用全可控电力电子变流器，转子电压和电流矢量的旋转角速度ωr完全可控，因此控制ωr就可以控制双馈电机定子的有功功率。

有功功率给定和实际的有功功率相减之后通过PI控制器得到转子电压的频率;

从式（12）和（13）中的第三项可以看出，双馈电机的暂态励磁电压E`q和转子电压的大小有关。转子电压Edf部分表示无功励磁分量，而Edf表示在变频过程中，转子侧需要提供的电压，这部分电压和转子侧提供的转差有功功率相关。改变转子电压的幅值可以改变E`q进而改变定子发出的无功功率［17-20］。

根据式（11）可知，双馈电机定子的无功功率主要和定子电压有关，因此可以在电压环外面加上无功功率外环。无功功率给定和实际无功功率相减之后通过PI控制器得到定子电压的给定值。定子电压给定和实际电压相减之后通过PI控制器得到转子电压幅值，有了转子电压的幅值和频率给定之后经过简单运算就可以生成转子的三相电压给定值uar，ub r，uc r，三相电压再通过PWM调制送到转子侧变流器。其控制框图如图5所示。

图5 有、无功功率控制的幅度频率控制策略框图

当然也可以将无功外环和电压环进行合并，无功功率控制器直接输出双馈电机转子电压的幅值。

5.2 仿真验证

为了验证图5中的控制策略，在PSCAD里面搭建模型进行仿真，仿真中用附录中的参数。电机定子有功功率给定在第2 s从2 kW阶跃到6 kW，然后在第9 s又阶跃回2 kW，定子无功功率给定为0 kVar并保持不变，双馈电机的转速为0.9倍的同步转速。仿真结果如图6所示。图中（a）～（d）分别表示定子有功和无功功率、转子电流、转子电压频率和双馈电机的功角。

图6 有功和无功功率控制的幅度频率控制仿真结果

从图6可以看出，有功功率给定变化前，双馈电机的转子电压频率等于转差频率5 Hz。当有功功率给定增大时，从图6（b）和（c）可以看出，双馈电机转子电压和电流的频率增加，使得图6（d）中的功角增大，定子有功功率增加。由于无功控制器的作用，定子无功功率经过暂态的调节之后在稳态又回到0 kVar，当有功功率稳定在6 kW时，转子电压的频率又恢复到转差频率。在调节过程中，转子电压频率有一个振荡的过程，功角有一些超调。

当有功功率给定减小时，双馈电机转子电压的频率减小，功角减小，使得定子有功功率减小，定子无功功率经过暂态的调节之后在稳态又回到0 kVar，当有功功率稳定在20时，转子电压的频率又恢复到转差频率。在调节过程中，转子电压频率有一个振荡的过程。

从仿真结果可以看出，幅度频率控制可以独立控制双馈电机定子的有功和无功功率。

5.3 幅度频率控制在容错控制上的应用

幅度频率控制既可以直接控制并网后的双馈电机，也可以在角度传感器出现永久性故障的情况下作为容错控制策略。采用矢量控制和幅度频率控制组成的容错控制系统的逻辑图如图7所示，当容错控制系统判断角度传感器出现永久性故障时，就从矢量控制切换到幅度频率控制策略。

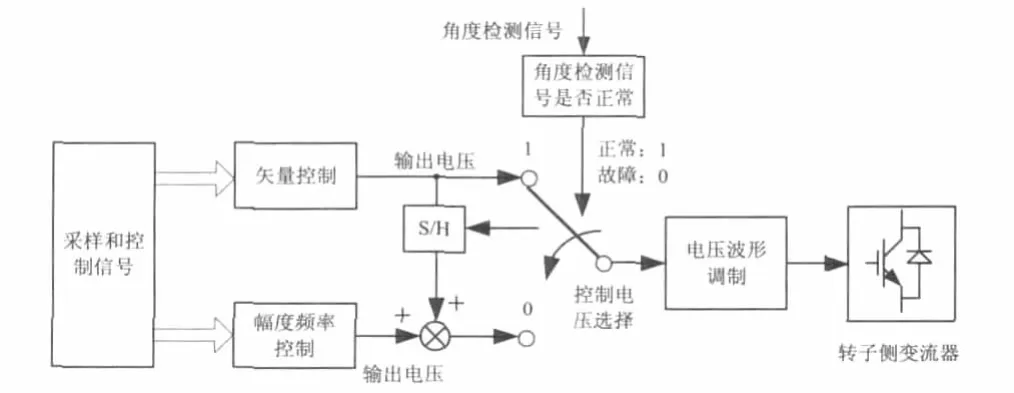
图7 幅度频率控制用于容错控制逻辑框图

正常情况下控制系统采用矢量控制，转子电压选择矢量控制的输出电压，当角度传感器出现永久性故障时，转子电压就选择幅度频率控制的输出电压。由于幅度频率控制刚投入时输出的电压为0，为了保证切换过程尽可能地平滑，需要计算出故障前矢量控制输出电压的幅值|ur0|和频率ωr0，将它们作为初始值分别叠加在幅度频率控制的输出上。其中|ur0|叠加在无功功率控制器输出上，ωr0叠加在有功功率控制器的输出上，如图8所示。幅度频率控制的采样和控制信号与矢量控制完全相同。

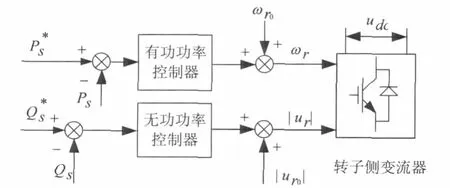
图8 幅度频率控制用于容错控制框图

在PSCAD里建立模型，对图7和图8所示的容错控制系统进行仿真。电机参数为附录中的参数，定子电压为380 V。控制系统先采用矢量控制，有功功率给定为6 kW，无功功率给定为0 kVar，双馈电机转速为0.9倍的同步转速，故障出现以前控制系统已经达到稳态。在第5 s角度传感器出现永久性故障，根据图7容错控制系统切换到幅度频率控制，并将故障前的转子电压的幅值和频率作为初始值叠加到幅度频率控制的输出，如图8所示。

仿真的结果如图9所示，图中（a）～（d）分别表示定子有功和无功功率、转子电流、转子电压频率和双馈电机的功角。按照图7和图8的容错控制方法，当角度传感器出现永久性故障时，可以用幅度频率控制代替矢量控制，控制策略切换的过渡过程比较平稳，满足容错控制的要求。

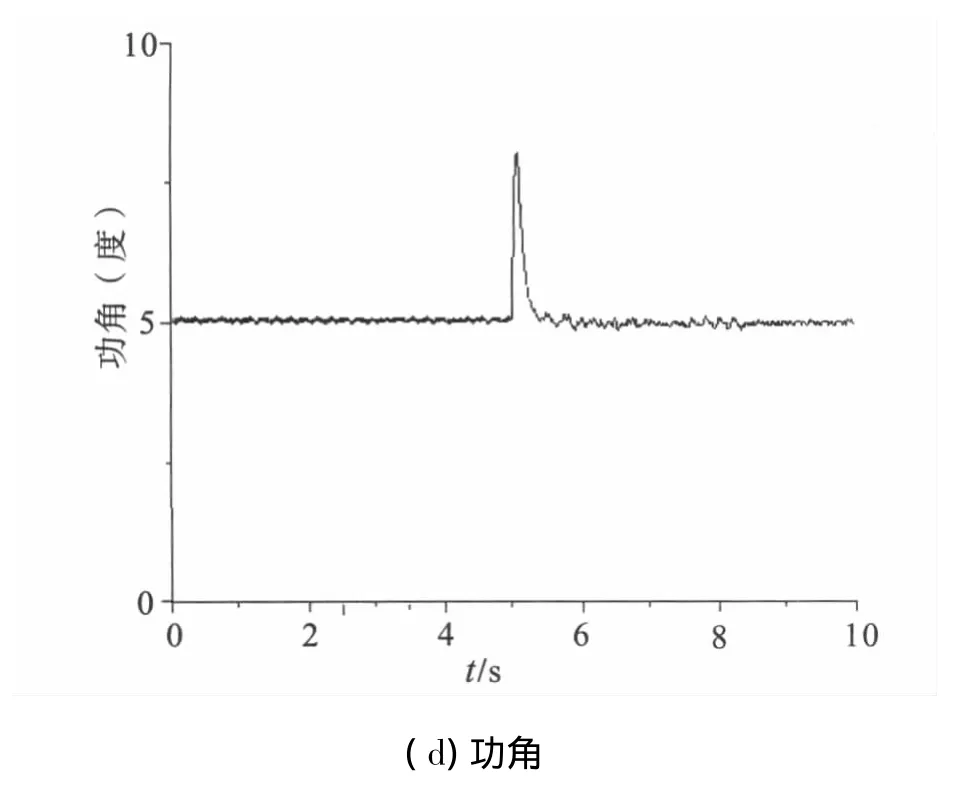
图9 幅度频率控制用于容错控制的仿真结果

6 结论

双馈电机以其自身显著的优点，成为现在风电的主力机型之一，并且由于双馈电机具有一定的同步机特性，可以从同步机类比的角度讨论新的控制策略。具体研究内容如下:

1）简述了双馈电机变速恒频原理及其dq坐标系下数学模型，简要分析了双馈电机网侧变流器和转子侧变流器的矢量控制策略。

2）根据双馈电机dq坐标系下的模型，推导了同步化双馈电机数学模型，归纳了双馈电机与同步电机的异同点。

3）基于同步化模型提出了幅度频率控制策略。此策略通过控制转子电压的幅值和频率来控制定子无功和有功功率，不需要角度传感器，简化了控制器设计，避免了转子角度编码器对发电系统的影响。

4）利用电磁暂态仿真软件PSCAD，验证了控制策略对双馈电机功率控制的有效性，并且分析了幅度频率控制在容错控制方面的性能，表明此控制策略满足容错控制的要求。

［1］孙元章，吴俊，李国杰.风力发电对电力系统的影响［J］，电网技术，2007，31（20）:55-62.

［2］贺益康，郑康，潘在平，等.交流励磁变速恒频风电系统运行研究［J］.电力系统自动化，2004，28（13）:55-59.

［3］李国杰，阮思烨.应用于并网风电场的有源型电压源直流输电系统控制策略［J］.电网技术，2009，33（1）:52-55.

［4］李晶，宋家骅，王伟胜.考虑变频器特性的变速恒频双馈风力发电机组控制策略的研究与仿真［J］.电网技术，2004，28（21）:11-16.

［5］MullerS，Deicke M，De Doncker R W.Doubly fed induction generator systems for wind turbines［J］.IEEE Ind Appl.Mag，2002，17（1）:26-33.

［6］LieXu，P.Cartwright，"Direct active and reactive power control of DFIG for wind energy generation，"IEEE Transactions on Energy Conversion，vol.21，no.3，pp.750-758，Sept.2006.

［7］Z.Dawei and X.Lie，"Direct Power Control of DFIG With Constant Switching Frequency and Improved Transient Performance，"Energy Conversion，IEEE Transaction on，vol.22，pp.110-118，2007.

［8］O.Anaya-Lara，F.M.Hughes，N.Jenkins and G.Strbac，"Contribution of DFIG-based wind farms to power system shortterm frequency regulation，"Generation，Transmission and Distribution，IEE Proceedings-，vol.153，pp.164-170，2006.

［9］F.M.Hughes，O.Anaya-Lara，N.Jenkins and G.Strbac，"Control of DFIG-based wind generation for power network support，"Power Systems，IEEE Transactions on，vol.20，pp.1958-1966，2005.

［10］O.Anaya-Lara，F.M.Hughes，N.Jenkins and G.Strbac，"Provision of a synchronising power characteristic on DFIG-based wind farms，"Generation，Transmission ＆ Distribution，IET，vol.1，pp.162-169，2007.

［11］F.M.Hughes，O.Anaya-Lara，N.Jenkins and G.Strbac，"A power system stabilizer for DFIG-based wind generation，"Power Systems，IEEE Transactions on，vol.21，pp.763-772，2006.

［12］P.Ledesma and J.Usaola，"Effect of Neglecting Stator Transients in Doubly Fed Induction Generators Models，"Energy Conversion，IEEE Transaction on，vol.19，pp.459-461，2004.

［13］R.Cardenas，R.Pena，J.Proboste，G.Asher and J.Clare，"MRAS observer for sensorless control of standalone doubly fed induction generators，"Energy Conversion，IEEE Transaction on，vol.20，pp.710-718，2005.

［14］S.Baike and O.Boon-Teck，"Novel Sensorless Decoupled P-Q Control of Doubly-Fed Induction Generator（DFIG）Based on Phase Locking to Gamma-Delta Frame，"in Proc.2005 Power Electronics Specialists Conference，2005.PESC ＇05.IEEE 36th，pp.2670-2675.

［15］Akhmatov V.Analysis of dynamic behaviour of electric power systems with large amount of wind power［D］.Denmark:ElectricPower Engineering，Orsted-DTU，Tech.Univ.Denmark，Kgs.Lyngby，2003.

［16］王中，李国杰，孙元章，等.转子角度偏差对双馈风力发电系统稳定性的影响［J］，电网技术，2010，32（12）:147-153.

［17］Ekanayake J and Jenkins N.Comparison of the response of doubly fed and fixed-speed induction generator wind turbines to changes in network frequency［J］.IEEE Trans.on Energy Conversion，2004，19（4）:800～802.

［18］（俄）Ю.Г.夏卡梁著，徐绳均译.异步化同步电机［M］.北京:中国电力出版社，1997.

［19］高景德，王祥珩，李发海.交流电机及其系统的分析［M］（第二版）.北京:清华大学出版社，2005.

［20］Qiang Lu，Yuanzhang Sun and Shengwei Mei.Nonlinear control systems and power system dynamics.London:Kluwer academic publishers，2001.

［21］倪以信，陈寿孙，张宝霖.动态电力系统的理论和分析［M］.北京:清华大学出版社，2002.

［22］Prabha Kundur.Power System Stability and Control［M］，1st E-dition.New York:McGraw-Hill，1994.