某新型火炮发射过程建模与仿真
2013-10-14刘圣杰张相炎
刘圣杰,张相炎
(南京理工大学机械工程学院,江苏南京 210094)
0 引言
现代战争对火炮的综合性能提出很高的要求,但是火炮的威力与机动性能等条件通常是相矛盾的。如何协调好它们之间的关系,是提高火炮综合性能的关键。根据无后坐力炮与膨胀波火炮在发射过程中都有火药气体流出的技术特点,提出了一种新型火炮,在火炮发射过程中的某一膛压下使火药气体向后喷出,产生一个向后作用的冲量,这样起到协调火炮威力与机动性能的关系。该炮的发射过程不同于无后坐力炮与膨胀波火炮,本文针对其特点建立其发射模型,并分析其发射性能。
1 物理模型
该型火炮采用半可燃药筒,发射时药筒卡在膛内,火炮发射过程中火药燃烧膛内压力增大,当达到半可燃药筒金属筒底的许用剪应力时,半可燃药筒被剪断,在高膛压下,半可燃药筒的金属筒底与火药气体同时向后喷出。其发射过程可以分为以下几个阶段:第一阶段,底火点燃发射药,达到弹丸的启动压力后推动弹丸向前运动,这一过程与普通闭膛火炮一样;第二阶段,当膛压到达半可燃药筒金属筒底的剪断条件时,金属筒底被剪断后火药气体喷出,膛内火药气体流动状态发生改变,膛内压力迅速下降,同时弹丸继续向前运动,直到出炮口;第三阶段,即弹丸出炮口后的后效期阶段。
图1是根据该新型火炮的特点而简化的物理模型。
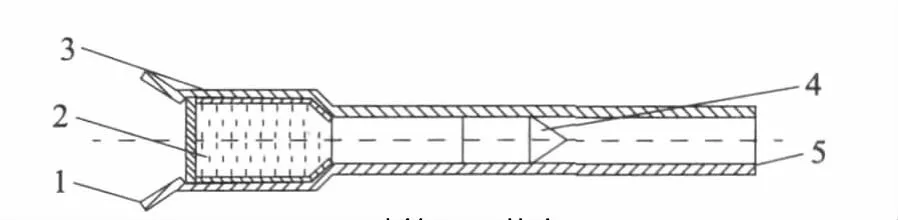
图1 火炮的结构示意图
2 数学模型
该型炮的发射过程不同于其他火炮,由于采用半可燃药筒,燃烧过程需考虑其对发射过程的影响。且在发射的最大膛压时期有火药气体喷出,同时炮尾处增加了提高气流喷出速度的拉瓦尔喷管,其发射过程的物理化学现象显得相当复杂。为了近似计算它的发射过程,需要对其进行一定的假设与简化:该模型基于内弹道零维模型,运用经典内弹道理论进行建模与计算。
2.1 半可燃药筒燃烧模型[1]
该弹药采用半可燃药筒技术,主要有金属筒底、可燃药筒、底火、主发射药及弹丸等组成。半可燃药筒在火药燃烧时会连同药筒一起燃烧。假设半可燃药筒符合几何燃烧定律,并由内向外燃烧。可将半可燃药筒装药当作是一种混合装药,现将半可燃筒体简化成一圆柱体(图2)。
则可推导出半可燃药筒的形状特征量:

其中:D0,d0分别为半可燃药筒的外径与内径;c0为半可燃药筒的筒壁厚;c为半可燃药筒的筒长。

图2 半可燃药筒简化模型
2.2 半可燃药筒剪切受力分析
在膛内火药气体压力的作用下,半可燃药筒金属筒底的受力如图3所示。其中,pt为膛底压强;L为半可燃药筒金属筒底的厚度。
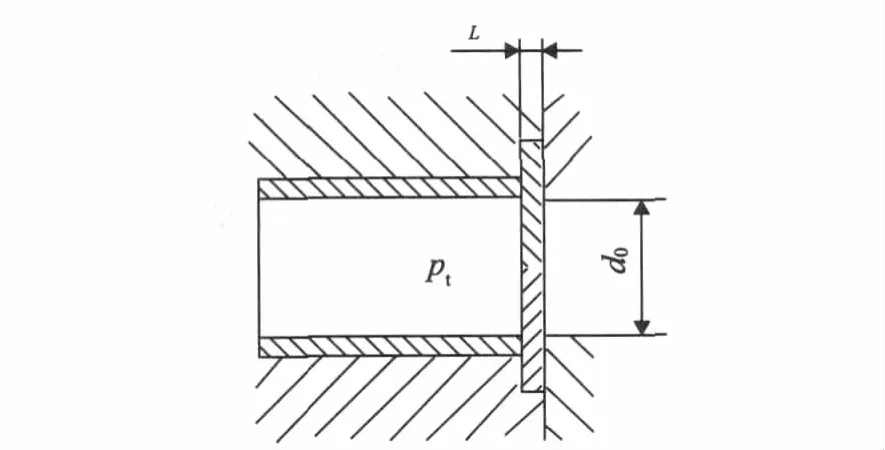
图3 半可燃药筒剪切受力计算简图
在膛底压强pt的作用下,金属筒底所受到的剪应力为:

若金属筒底所用材料的许用剪应力为[τ],则金属筒底被剪断时的膛底压强为:

2.3 该型火炮膛内压力分布假设[2]
火炮在射击过程中有大量火药气体流出。气流向两端流动,在炮膛的某一断面会存在一滞止点,并假设膛内密度均匀分布。其压力分布为:
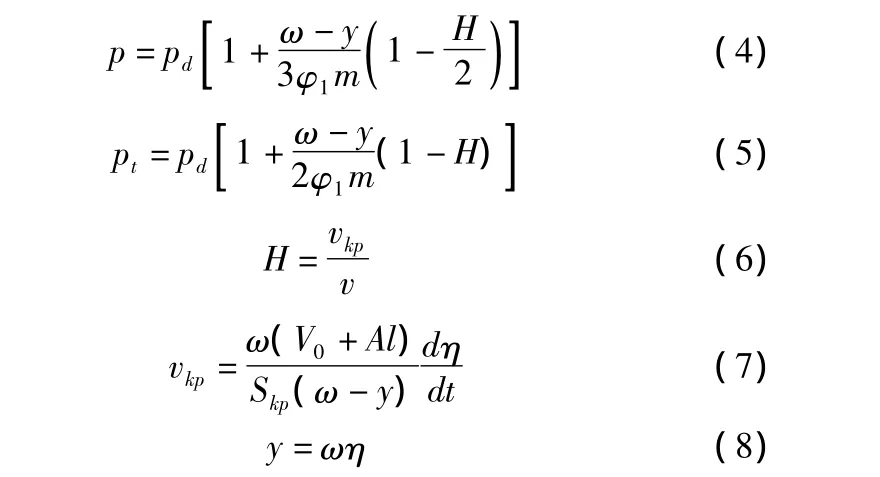
该膛内压力分布条件同样适用于炮尾无火药气体流出的常规火炮,其中:p为膛内平均压力;pd为弹底压力;ω为装药量;y为火药气体流出量;φ1为阻力系数;m为弹丸质量;H为速度比;vkp为炮尾喷管火药气体临界流速;Skp为喷管临界断面积;η为火药气体相对流出量;A为炮膛断面积。
2.4 内弹道基本方程[2-4]
火药形状函数:
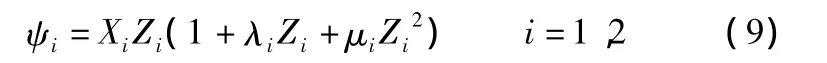
其中:ψi为火药已燃相对质量;Zi为火药已燃相对厚度;Xi,λ,μi为火药形状特征量;i=1,2 分别表示主装药与半可燃药筒。
火药燃速方程:

其中:ui为火药燃速系数;ni为火药燃速指数。
弹丸速度与行程方程:
其中:l为弹丸行程;t为弹丸运动时间;v为弹丸速度。
弹丸运动方程:

其中:S为炮膛截面积。
能量守恒方程:
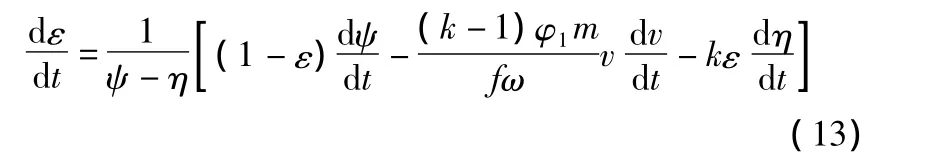
其中:ε为相对温度;η为火药气体相对流量;k为绝热指数;f为火药力。
燃气状态方程:

其中:lψ为药室自由容积缩径长;l0为身管长;Δ为装填密度;ρpi为火药密度;αi为气体余容。
炮尾火药气体流量方程:

其中φ2为消耗系数。
3 数值计算与仿真结果分析
以某35 mm膨胀波火炮的参数为计算依据,其具体初始计算数据可参考文献[2]。半可燃药筒金属筒底的材料采用 H62 黄铜,其 σb=294 MPa,取[τ]=σb=98 MPa。
为检验上述模型的正确与否,现将计算曲线与35 mm膨胀波火炮实验曲线作比较,从图4可以看出,由于半可燃药的燃烧,会导致最高膛压相比会大点,模型基本满足要求,所以上述模型能用于实际计算。
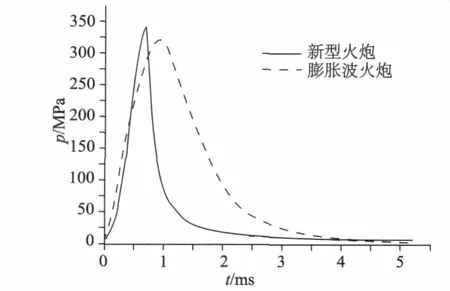
图4 与膨胀波火炮的膛压—时间对比曲线
3.1 半可燃药筒金属筒底厚度对发射性能的影响
根据上述数学模型,通过Matlab编程进行数值计算,可以得到相关的内弹道数据。图5是不同的半可燃药筒金属筒底厚度计算出的弹丸速度曲线。

图5 不同金属筒底厚度下的弹丸速度—行程曲线
从图5可以看出,随着金属筒底厚度的增加,弹丸初速相应增加,但当达到一定的值时不再变化,这是由于金属筒底厚度的增加必然会导致剪断压强的增加,即火药气体喷出时间向后的延迟,这样进一步增大弹丸的初速。当厚度达到一定程度时,半可燃药筒金属筒底不被剪断,其过程与闭膛火炮一样,无火药气体的喷出,故发射性能不再变化。图6是不同的金属筒底厚度与弹丸速度的大致关系。

图6 弹丸初速与金属筒底厚度关系图
3.2 最佳剪断条件下该型火炮与常规火炮性能比较
为了获得在剪断条件下的最大弹丸初速,必须尽量使金属筒底的厚度刚好满足在闭膛下的最大膛压,此时刚好被剪断,该新型火炮获得最大弹丸初速,达到最佳剪断条件。
图7是最佳剪断条件下该型火炮与同口径闭膛火炮的膛压曲线,由于在火药气体未喷出前,该新型火炮的发射过程与常规火炮一样,其膛压曲线重合。当达到最大膛压341.01 MPa时,即在内弹道时间 0.68 ms,火药气体向后喷出,膛内压力急剧下降。这比较符合实际情况。
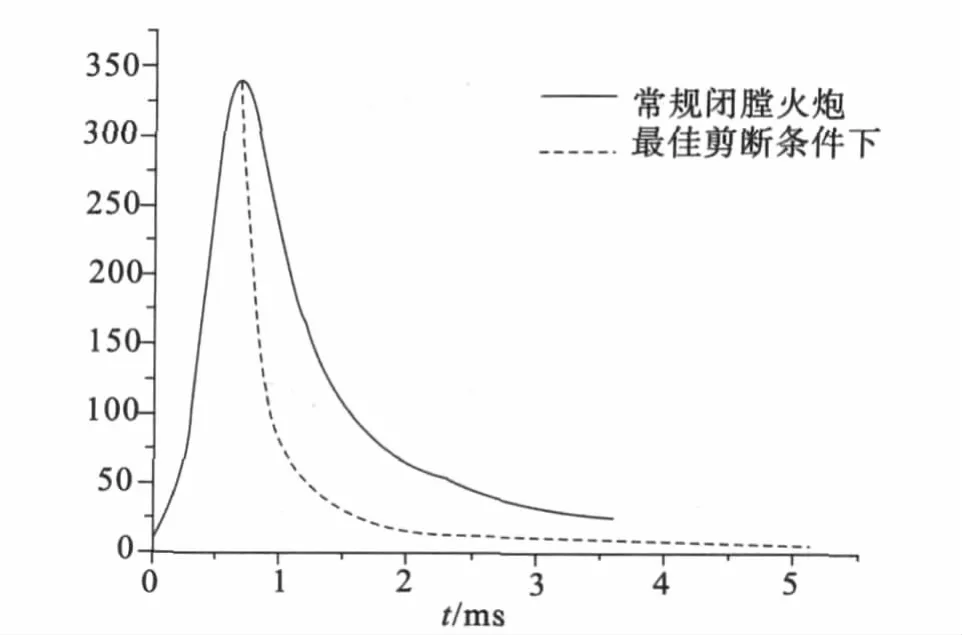
图7 与常规闭膛火炮的膛压—时间对比曲线
图8是在该条件下与常规火炮的弹丸速度与行程关系的对比曲线,由于火药气体在最大膛压时喷出,膛内压力下降,弹丸在膛内相比闭膛火炮没有得到足够的加速,因此弹丸的初速要比闭膛火炮小。
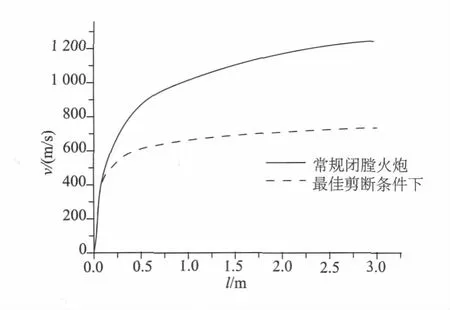
图8 与常规火炮的弹丸速度-行程对比曲线
根据膛内压强可以计算出火药气体在炮膛轴线上的作用力,在炮膛闭合时的火药气体作用力为F=p·A,当火药气体喷出时的作用力为火药气体对喷管的推力F=-ξ·Skp·p,其中ξ为推力系数。
图9是该条件下与常规闭膛火炮的火药气体作用力的对比曲线。图中虽然火药气体在炮膛轴线方向的最大力没有发生改变,但在火药气体喷出后,火药气体作用力的方向反向,这对于反后坐装置的设计能带来极大的好处。

图9 与常规闭膛火炮的火药气体作用力-时间对比曲线
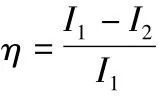
4 结语
该型火炮虽然牺牲了部分的弹丸初速,但是极大地减小了火炮发射过程中火药气体的作用冲量,对于不同要求的火炮武器系统具有重大意义。本文主要建立了它的发射模型,并以某35 mm口径炮作为原型进行了数值仿真。对于该型火炮的进一步研究与工程实际应用具有参考作用。
[1]张才友.全可燃药筒高速发射内弹道性能仿真[D].南京:南京理工大学,2008.
[2]金志明.枪炮内弹道学[M].北京:北京理工大学出版社,2004.
[3]王颖泽,张小兵,袁亚雄.膨胀波火炮后喷装置流场性能分析[J].兵工学报,2009,30(5):525-530.
[4]KATHE E.Sonic rarefaction wave recoilless gun system [P].US.Patent:6460446B1,2002-10-08.
[5]DILLON R,KATHE E.Sonic rarefaction wave low recoil gun[R].AIAA2001-0743,2001.
[6]支建庄,郑坚,狄长春,等.惯性炮尾式膨胀波火炮膨胀波速度和行程计算仿真[J].火炮发射与控制学报,2009(1):5-8.
[7]张帆,廖振强,刘国鑫,等.膨胀波枪炮发射性能若干影响因素的研究[J].兵工学报,2008,29(1):23-27.
