重型数控落地铣镗床主轴组件温度场分布建模

邓健，刘一磊，高栋

（哈尔滨工业大学机电工程学院，黑龙江哈尔滨 150001）

0 引言

重型数控落地铣镗床由于其开放式的加工方式、大功率切削等特点，广泛应用于航天、国防等领域。随着对加工效率的要求不断提高，高速化已成为落地铣镗床的一个主要发展趋势。主轴组件作为机床的核心部件，随着主轴转速的提高，其温度和热变形也愈加显著，会严重影响机床的加工精度。目前，许多学者开展了机床主轴热特性的研究工作，取得了一定的进展［1-3］，但是针对重型数控落地铣镗床热特性的研究还较少。

针对重型数控落地铣镗床主轴组件的热特性进行分析，首先研究了主轴组件热边界条件的确定方法，在此基础上建立了主轴温度场有限元分析模型，并进行了实验研究，通过相同的工况下实验结果与模型计算结果的对比分析，建立了有限元模型对流系数的修正方法，为后续主轴组件热特性分析作准备。

1 主轴组件热源及边界条件确定

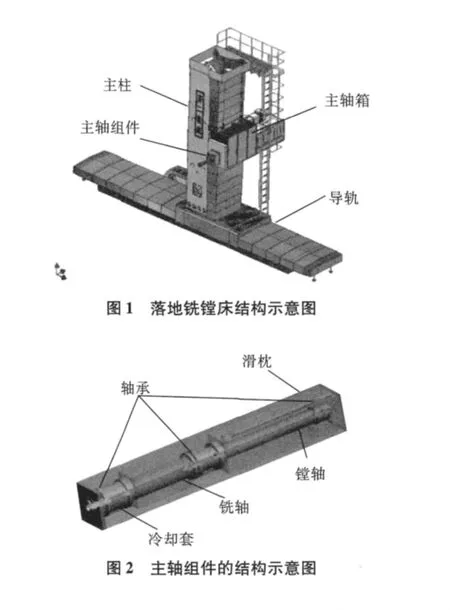
主轴组件位于机床的主轴箱内，由滑枕、铣轴、镗轴、轴承、冷却套等几部分组成，其结构形式如图1和图2所示。主轴组件内部的主要热源为主轴轴承的摩擦热，轴承产生的热量一部分通过对流换热被润滑油带走，另一部分则通过主轴与滑枕传递到机床的其他部分。

1.1 轴承生热量计算

重型数控落地铣镗床主轴组件中采用了三种型号的轴承，分别为 B71956、B71952 和 7926C。Palmgren［4］推导了计算轴承生热量的经验公式:

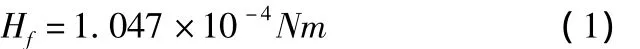
式中:Hf为轴承发热量 （w），n为轴承转速 （r/min），M为轴承摩擦力矩（N·mm）

在有限元分析中，热载荷是以体生热率qv加载的:

式中:Hf为轴承生热率;V为模型中轴承的计算体积。三种轴承和生热率的表1所示。

表1 轴承生热率

1.2 对流换热系数的计算

根据努谢尔特准则［5］，对流换热系数 h的计算公式为:

式中:λ为流体导热系数，Nu为努谢尔特数，L为特征尺寸。

努谢尔特数Nu反映了物体间的实际换热条件，可根据机床实际情况，利用传热学理论求得。表2所示是主轴各部分的对流系数计算结果。

表2 主轴组件各部分对流系数计算结果

2 主轴组件温度场有限元分析

2.1 有限元模型的建立

首先在三维制图软件PRO－E中建立主轴组件的三维模型，然后导入ANSYS软件进行主轴组件热稳态分析，初始温度设定为17℃，主轴转速1 000 r/min。热分析单元采用SOLID70三维热实体单元，该单元由8个节点组成，具有描述三维热传导的功能。为保证分析质量，在网格划分中优先使用六面体单元网格。将计算得到的轴承生热率作为体载荷，对流系数作为边界条件施加到有限元模型上，得到主轴组件的稳态温度场如图3所示。可以看到，轴承产生的热量沿着主轴和滑枕向主轴组件其他部分传递，呈现出明显的温度梯度。由于前轴承所受载荷最大，因此主轴组件达到热平衡时，前轴承处的温度最高，与实际情况相符。

图3 主轴组件稳态温度场分布

2.2 对流系数的实验修正

由于机床的结构和工作环境比较复杂，包含了许多不确定因素，因此将有限元分析与实验的方法相结合，采用正交实验方法，对有限元模型的热边界条件进行修正，使其能够更加精确地反映机床的热特性。

由于镗轴前端锥孔和滑枕外壁靠近前轴承处的温度与主轴与滑枕的热伸长密切相关，因此利用这两处的温度对模型进行修正。令机床以1 000 r/min转速空转，每半小时记录一次温度，分别记为 ai，bi（i=1，2，…，10）。

当主轴转速1 000 r/min时，根据对流散热性质不同，可由经验大致确定各部分对流系数的取值范围［6］:主轴组件与空气间的自然对流系数:1－30W/m2℃，与空气间的强制对流系数:20－150W/m2℃，与润滑油间的强制对流系数:50－300W/m2℃。首先在经验取值范围内，在各对流系数的计算值附近各选取4个值作为水平，建立L16（45）正交实验表。将正交表中各组实验参数带入有限元模型进行瞬态温度分析，得到与实验点相对应处节点的温度变化，分别记为 Xi，Yi（i=1，2，…，10）;取其与 ai，bi的差方和u作为正交实验的指标。

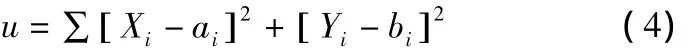
u表征了模型计算值与实验值的偏差，故其值越小，对应的因素水平越优。由表3可知，各组实验结果中u的最大值为371.53，最小值为 37.3，最小值对应的水平组合（20，25，100，150，200）即为已进行实验中的最优水平组合。由各因素水平的均值可绘制出效应曲线图，如图4所示。

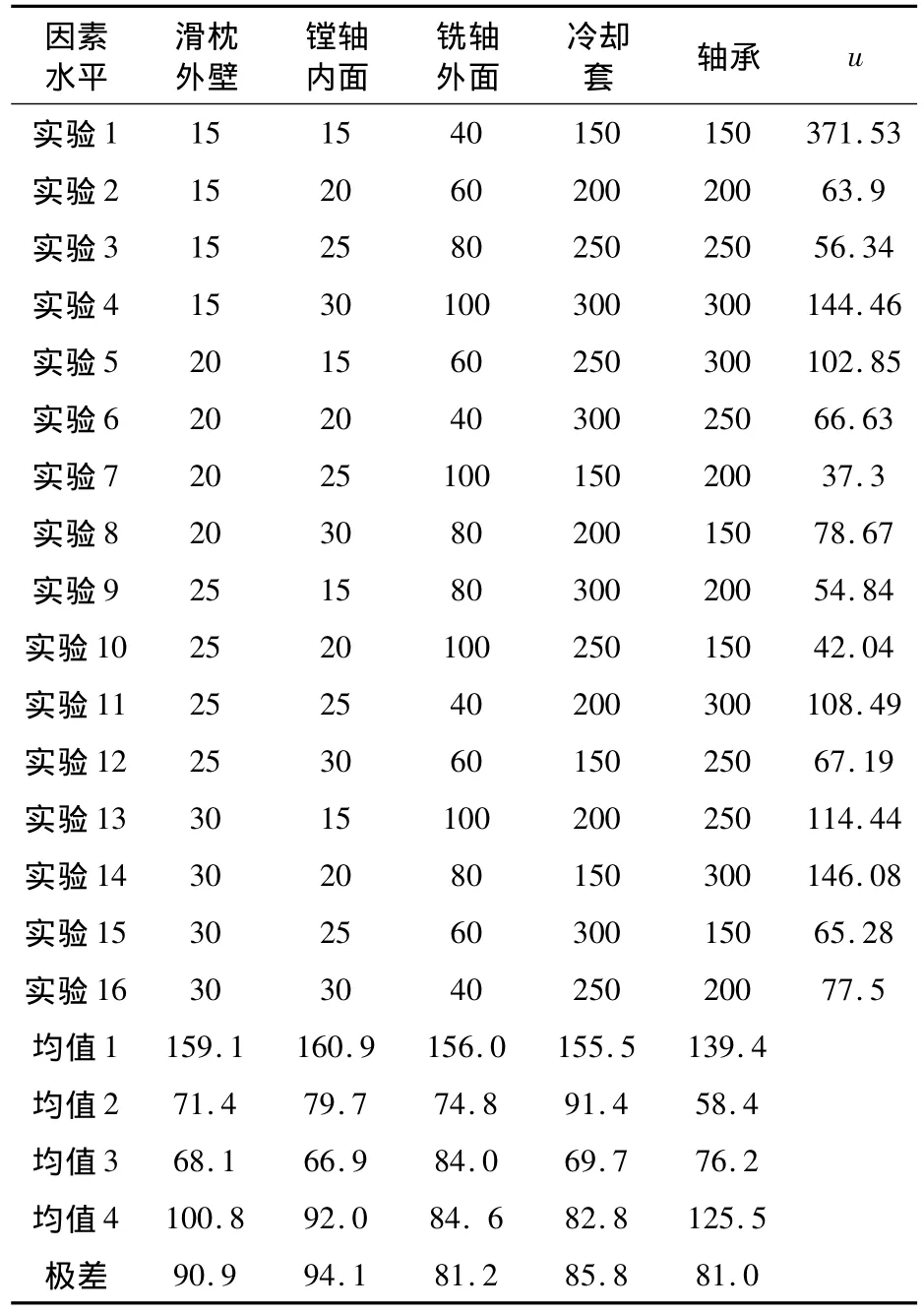
表3 试验1正交实验表

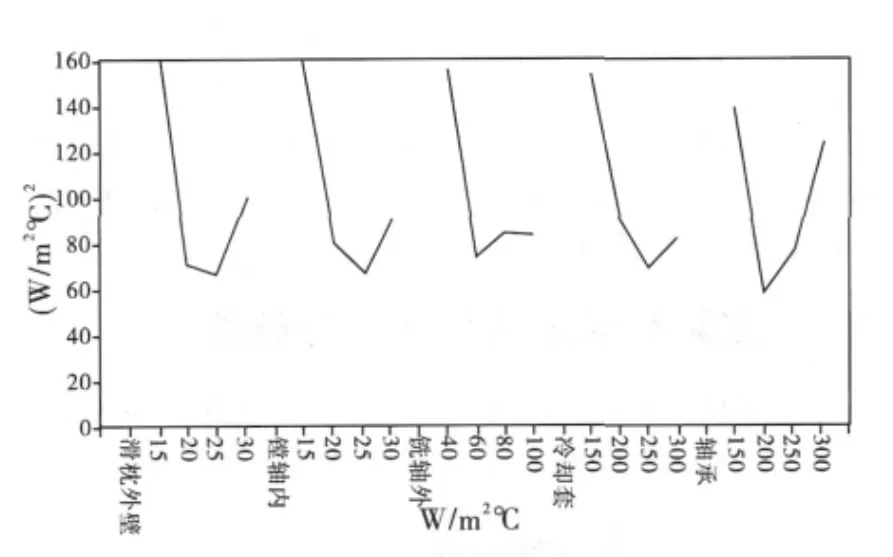
图4 试验1效应曲线图

效应曲线图反映了各因素水平的变化对u的影响，因此效应曲线的最低点所对应的水平组合（25，25，60，250，200）为推测的较优水平组合。将这一组对流系数带入有限元模型进行验算，发现其指标u值为54，并非最优组合，因此需进行进一步试验。

在试验1中推测出的较优水平附近继续取值，并缩小水平变化间隔，进行第二轮正交实验。由于镗轴内面对流系数这一因素推测出的较优水平正是已进行实验中的最优水平，并且水平间隔已较小，故可确定其取值。为简化实验，在下次实验中去除这一因素。

由表4可知，正交试验2中u的最大值为64.71，最小值为38.69，其变化范围明显缩小，说明在当前水平间隔下，各因素对u的影响已较小。根据本论试验结果绘制的曲线效应图，可推出一组可能的较优参数组合（23，80，210，200）。将这组对流系数带入有限元模型进行验算，得到u的值36.9为目前最小，因此取其为校正后的对流系数（图5）。

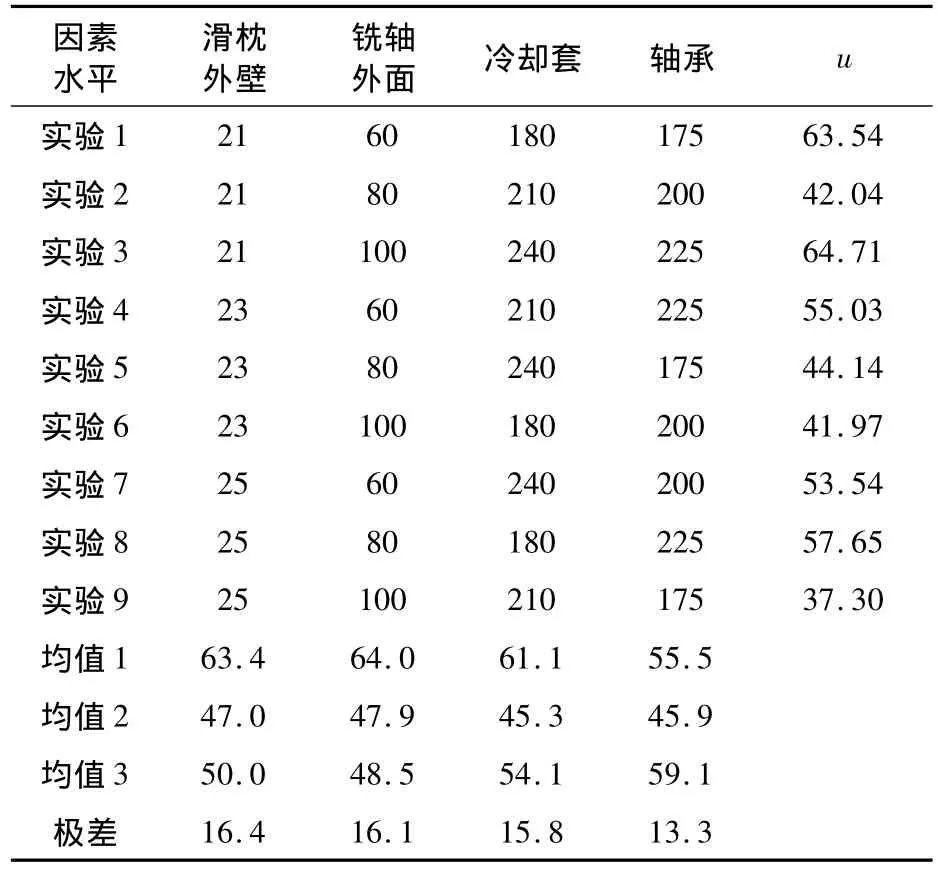
表4 试验2正交实验表

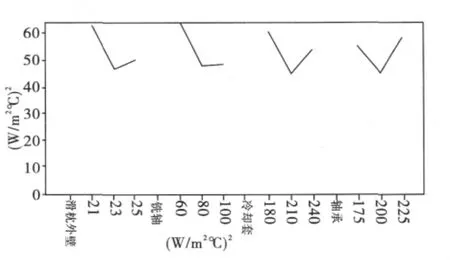
图5 试验2曲线效应图

如图6和图7所示，校正后有限元分析结果更加接近实验结果，但仍存在一定的误差，分析原因如下:

1）有限元模型为了便于分析，进行了简化，对主轴组件的温升规律产生一定的影响。

2）这里只考虑了主轴组件的热特性，未考虑主轴部分向机床其他部分的热量传递，也会产生误差。

3）实验数据受环境因素，测量因素等影响也会存在一定的误差。

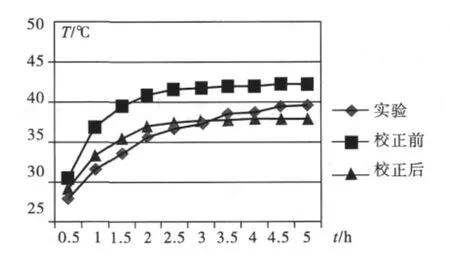
图6 参数校正前后的滑枕温度计算结果对比图

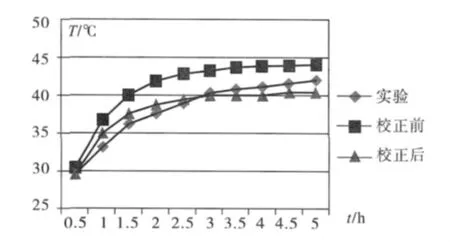
图7 参数校正前后的镗轴温度计算结果对比图

3 结论

本文建立了重型落地铣镗床的温度场分布的有限元分析模型，研究了主轴轴承生热量和热边界条件的确定方法。提出了利用正交试验分析的方法，根据机床主轴系统实测温度与仿真计算结果的比对分析，对有限元模型中的对流系数进行调整，有效的提高了主轴组件有限元模型的计算精度，为准确掌握机床主轴组件的热态特性打下了坚实的基础。

［1］石彦华，周华.CXK630五轴联动车铣复合加工机床高速主轴热态特性分析［J］.机床与液压，2009（6）:35-37.

［2］刘国庆，杨庆东，王科社.五轴加工中心主轴的热性能虚拟仿真研究［J］.北京机械工业学院学报，2000（12）:24-28.

［3］曹骏.HTM850G数控加工中心主轴系统的热特性研究［D］.杭州:浙江大学硕士学位论文.2007.

［4］Harris T A.Rollingd Bearing Analysis［M］.New York:John Wiley ＆Sons，inc，2001.

［5］黄晓明.高速电主轴热态特性有限元分析［D］.广州:广东工业大学硕士学位论文，2003.

［6］吴佳燕，李郝林.改善数控机床主轴系统热特性有限元分析精度的方法［J］.工具技术，2010，44（3）:30-33.