我国周边海域典型海洋锋特征建模研究

卢晓亭 , 濮兴啸, 李玉阳

(1.海军潜艇学院, 山东 青岛266071; 2.总参气象水文局, 北京100081; 3.中国白城兵器试验中心, 吉林 白城137000)

海洋锋是特征明显不同的两种或几种水体之间狭窄的过渡带[1]。在海洋锋区, 由于海水的温度、盐度在水平方向存在强烈的变化, 海洋锋存在明显的时空间特征变化, 导致锋区声速具有明显的水平梯度变化, 从而将显著改变水下声传播的方向和距离,引起声纳探测水下目标方位和距离的改变, 所有这些都对声纳的水下探测和反探测产生显著影响, 而目前还没有有效的实时估计获取锋区水下三维温、盐结构的方法。特征模型提供了一种解决这类问题的方法, 特征模型是充分利用遥感数据和有限的实测数据及历史数据, 结合目前已统计分析得出的海洋锋典型结构特征, 基于海洋锋空间几何结构数学模型快速有效获取海洋锋精细三维结构特征的方法[2]。Bennett和 Carnes[2-3]对湾流锋和冰岛-法罗锋特征模型做了相关研究, Gangopadhyay和Robinson等[4-6]对特定区域海洋锋特征模型做了研究。在国内, 菅永军等[7]以 Gangopadhyay海洋锋特征模型为基础, 建立了海洋锋区声速计算的理论模式。本文利用统计方法分析海洋锋年平均特征, 并结合海洋锋空间结构几何模型, 建立适用于我国周边海域典型海洋锋特征模型, 快速计算锋区温度场。

1 海洋锋特征模型

1.1 理想特征模型

理想特征模型(模型1)依据海洋锋区典型位置点温度剖面变化特征来构造特征模型。典型位置即锋区近岸侧边界、锋区中心、锋区离岸侧边界对于特定位置i(x,y)深度z处的温盐结构由下式给出[4]:

其中,T代表温度,i分别代表锋一侧边界、锋区中心、锋另一侧边界, 下标s, b分别代表海表和海底(或锋区下界),φi(z)是无维水温剖面, 在z=0时取值为1,z=H(H为海底或锋区下界深度)时取值为 0。例如黄海海水水温垂直剖面可大致分为三层: (1)上均匀层; (2)温跃层;(3)下均匀层, 利用最小二乘法分段拟合无维水温剖面:

其中,a1, … ,c3为经验系数, 通过大量历史数据统计分析确定;h代表上均匀层的下界;Z是温跃层下界深度,H为海底深度。分别计算得到海洋锋两侧边界处和锋区中心处的 3个典型位置温度剖面后,其他锋区位置点剖面, 根据位置点到锋中心轴的距离, 进行线性插值计算。

1.2 陆架坡折锋特征模型

陆架坡折锋是高温陆架水和低温陆坡水边界处形成的的跃迁带。它往往处于陆架坡折附近, 阻隔着外海和陆架水的水平交换。陆架坡折锋主要结构特征包括: 由卫星遥感数据海表温度SST、多通道海表温度MCSST提取的海洋锋海表统计的平均位置; 由温度或盐度等值线确定的锋底部平均位置、锋的坡度、宽度及锋区温度混合的形式。锋区三维温度分布形式为(模型2)[6]:

混合方程为:

其中:

其中,Tsh代表陆架区温度剖面,Tsl代表陆坡区温度剖面,z代表深度,η是从锋中心轴到分析位置的宽度,m是双曲正切形式的混合函数,θ是锋的坡度,γ是锋的宽度,xf是水平距离,h是垂直距离。

1.3 沿岸流锋特征模型

沿着局部浅海海岸流动的海流叫沿岸流, 它们是由河水和海水混合形成且具有淡水性质的低盐水流。低温、低盐沿岸水和高温、高盐外海水交汇的地方通常形成沿岸流锋, 中国近海典型的沿岸流锋面有黄海西部沿岸锋、江浙沿岸锋。沿岸流锋区温度或盐度的三维分布表示形式为(模型3)[7]:

式中,x为沿着流方向的坐标,y为与沿流方向坐标垂直的断面坐标,z轴为垂直坐标即由海表延伸至海底的坐标,α(x,z)为与流垂直方向上的振幅变化函数,Γ(y,z)代表温度水平梯度值,Ta(x,z)为锋区中心温度剖面函数,T0(x)主轴处海表温度,Tb(x)主轴位置底部温度,φ(x,z)为无维温度垂直剖面。

1.4 基于EOF重构温度剖面方法特征模型

分别根据锋区周围不同水体温度场建立锋区不同温度气候态, 通过海洋锋典型特征如锋宽度、坡度以及从计算网格节点到锋某一侧边界距离等建立加权函数, 通过对不同气候态的加权融合推断锋区温度剖面, 最后通过一系列温度剖面的集合来描述海洋锋的三维结构。

网格节点j在深度z的温度, 由下式给出[7]:

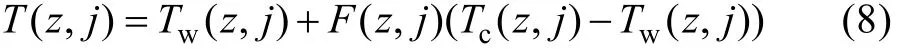
Tw,Tc为分别依据锋暖水侧、冷水侧的历史数据建立的气候态温度, 模型采用经验正交函数(EOF)和遥感SST数据来描述气候态剖面。假设在某个海域有N个已知的温度剖面样本, 每个剖面有k+1层, 则温度剖面样本的协方差矩阵可由下式来确定:

其中,T是位置点i、深度处n的加权平均值;,n为位置点i、深度处n的加权标准差, 表征位置点i和j之间的相关性。温度场就可通过经验正交函数来进行重构, 其特征向量V= [v0,v1,… ,vk]为重构模型的空间函数, 前三阶的特征向量可以很好地解释原始剖面, 因此, 任何一点的温度表示为(模型4):

上式中α即为时间函数, 可以利用距离预报点最近的观测点的完整温度剖面拟合出时间函数。公式(8)中,F是加权函数, 提供两气候态剖面的相对权重,如果网格节点在锋冷水侧, 则F(z)=1, 相反, 在锋暖水侧则F(z)=0, 锋区内的节点权重假设具有一个高斯加权函数的形式:

x,d分别为水平和垂直距离, 即分析点位置和所在深度到锋边界的距离, 锋海表以下边界由海表边界和历史数据统计分析后假定,W, D为锋的宽度和厚度, 由海表特征和历史数据确定。

2 模型仿真结果

东海黑潮锋和黄海西部沿岸锋是我国周边海域两类典型的海洋锋, 分别在上述海洋锋分布海域选取一温度观测断面作为模型仿真的对象, 其中, 东海 F701(29.98°N, 125.92°E)～F713(28.47°N, 129°E)断面 温 度 、 黄 海 A1(36.5°N, 122.1°E)～A10(35.9°N,122.7°E)2010年8月观测断面温度垂直分布见图1。

2.1 理想特征模型仿真结果

利用理想特征模型对东海 F701～F713断面温度进行仿真, 垂直断面温度仿真结果如图2 (模型1)所示, 模型和观测结果表明, 模型计算结果与实测数据符合较好, 锋区温度等值线的走向与实测基本一致。为了定量比较分析模型仿真结果和实测数据, 给出实验断面模型仿真剖面与观测剖面均方根误差如图3(模型1), 其均方根误差在2.5℃以内。

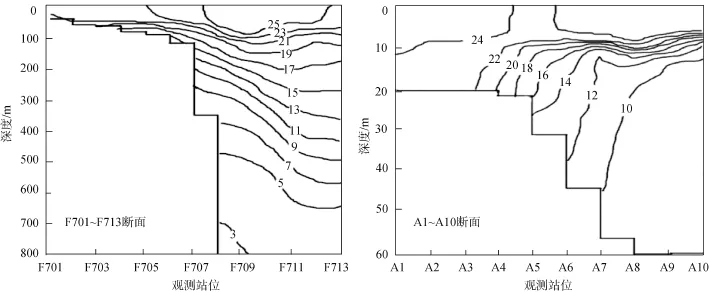
图1 断面温度(℃)垂直分布图Fig.1 The vertical temperature(℃)distribution of section

图2 特征模型仿真结果 (℃)Fig.2 The simulation results (℃)of feature models

2.2 陆架坡折锋特征模型仿真结果

选取与模型推测断面 A1～A10相同空间位置的观测断面进行对比验证分析, 结果见图 2(模型 2)。模型计算得到的温度等值线的走向基本与实测值相符合,海洋锋宽度、强度特征大致与实测数据相吻合, 坡度特征与实测相比偏大, 在温跃层深度内计算温度与实测值相比, 误差较大, 这与温跃层的不稳定性有很大关系, 其次, 与特征模型参数选择的理想化有关。图3 (模型 2)是均方根误差分布图, 均方根误差在 2℃以内, 说明了此特征模型的有效性, 可以满足一定的精度要求。

2.3 基于EOF重构温度剖面方法特征模型仿真结果

图2(模型3)给出图1F断面温度的特征模型计算结果。比较两图可以得出: 0～200 m层模型计算结果与实测数据吻合较好, 等温线的走向趋势与位置变化与实测值一致; 200至400 m层计算结果显示的锋区宽度小于实测值, 坡度与实测值吻合; 400 m以下水层, 等温线的走向与实测值还有一定差异。图3(模型3)说明其均方根误差在2.0℃以内由于东海黑潮锋北段主要位于200 m等深线以内的陆架区, 200 m以内均方根误差小于 1.5℃。因此, 该模型重构锋区温度比较理想。

2.4 沿岸流锋特征模型仿真结果

选取 A1～A10断面作为仿真断面, 图 2(模型 4)给出特征模型计算结果, 比较结果可以得出: 模型计算得到的温度等值线的走向与实测值吻合较好,锋宽度、强度、向下扩展的深度等特征也与实际值相符。图 3(模型 4)是均方根误差分布图, 均方根误差在2.5℃以内。

图3 模型仿真剖面与观测剖面均方根误差Fig.3 The RMS between the feature models and observations

3 小结

仿真结果表明: 理想化特征模型计算简单, 但对海洋锋温度剖面的重构精度不理想; 陆架坡折锋、沿岸流锋特征模型重构精度达到一定的要求, 这两类特征模型是基于海洋锋形成机制的基础上构建的,依据的是具体问题具体分析的原理, 因此, 结果较理想; 基于 EOF重构温度剖面方法特征模型, 要求使用EOF方法尽可能的精确重构基于不同水域经验正交函数系的区域海洋环境温度剖面, 在此基础上经过加权融合能够较好地重构锋区温度场。

[1]李风岐, 苏育嵩.海洋水团分析[M].青岛: 青岛海洋大学出版社, 2000: 87-88.

[2]Bennett T J, Carnes M R. Feature modeling: the incorporation of a front and eddy map into optimal interpolation-based thermal analyses [R]. Mississippi USA:Naval research laboratory stennis space center, 1988.

[3]Bennett T J, Boyd L, Knauer G, et al.A feature model of the iceland-faeroe front[J].Mar Tech Soc, 1992, 26(2), 44-52.

[4]Calado L, Gangopadhyay A, Robinson A R, et al. eatureoriented regional modeling and simulation (FROMS)for the western south atlantic: southeastern brazil region [J]. Ocean Modeling, 2008, 25: 48-64.

[5]Gangopadhyay A, Robinson A R. Feature-oriented regional modeling and simulations in the gulf of maine and georges bank[J].Continental Shelf research, 2003,23: 317-353.

[6]Gangopadhyay A, Robinson A R. Feature oriented regional modeling of oceanic fronts[J].Dynamics of Atmospheres and Oceans, 2002, 36: 201-232.

[7]菅永军, 张杰, 贾永君.海洋锋区的一种声速计算模式及其在声传播影响研究中的应用[J].海洋科学进展,2006, 24(2): 166-171.