对航姿参考系统的滤波方法研究

刘 禹

（船舶重工集团公司723研究所，扬州225001）

0 引 言

航姿参考系统（AHRS）是一种微型捷联惯导系统，可以在3D空间中测量平台的全角度方向，提供航向、俯仰和横滚信息。航姿参考系统采用微机电系统（MEMS）技术和磁阻传感器技术，成本低，体积小，集成度高，从而可以使得小型电子对抗设备这类对体积和成本敏感的系统具有航姿测量能力。由于成本和体积的约束，航姿参考系统输出的航向角等数据由于噪声的原因，误差通常较大，必须经过处理，才能达到使用要求。

1 卡尔曼滤波原理

卡尔曼滤波能够利用目标的动态信息，通过自回归数据处理算法，得到一个关于目标状态的最优估计。该估计可以是对过去状态的估计（平滑），可以是对当前状态的估计（滤波），也可以是对将来状态的估计（预测）。卡尔曼滤波算法以反馈控制的方法进行过程状态的估计：滤波器估计出过程中某一时刻的状态，然后以测量变量的方法获得反馈。卡尔曼滤波的递推最优估计方法［1］，采用状态空间描述法，在算法上采用递推形式，只需要很少的几个测量值和预测值就能进行最优的状态估计，因此在实时系统中能很好地对噪声起到滤波作用，适合处理航姿参考系统的输出数据。由于卡尔曼滤波器进行状态估计时，其动态方程和测量方程均为线性方程，状态可控，算法简练，十分适合工程应用［2］。下面对卡尔曼滤波方程进行分析。

在数学上，图1中的信号流程图至少可以表述为以下2个方程：

（1）过程方程：

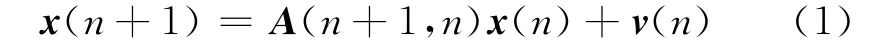
式中：M×1向量v（n）为过程噪声，按照高斯白噪声过程进行建模，其相关矩阵可定义为：

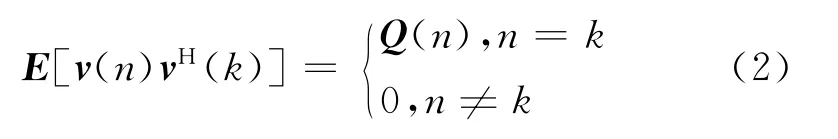
该线性动态系统可表达为2个反馈连接的独立单元，它们分别为：一个转移矩阵，用A（n＋1，n）来表达；一个存储单元，用z－1I来表达。其中，z－1为单位延迟，I为（M×M）单位阵。转移矩阵A（n＋1，n）表示系统从n时刻到n＋1时刻的转移过程。

（2）测量方程

观测向量可由下面的方程来表示：

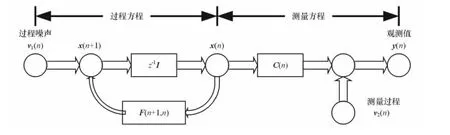
图1 线性动态离散时间系统的信号流程图

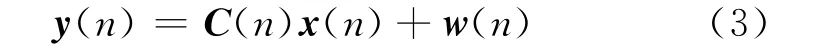
式中：C（n）为已知的N×M测量矩阵；N×1向量w（n）为测量噪声，按照高斯白噪声过程进行建模。

若i＝n，该问题称为滤波；若i＞n，称为预测；若1≤i＜n，则称为平滑。此处只考虑滤波和预测，它们是密切相关的。

实际算法中迭代步骤如下：

（1）新息过程

计算n时刻观测数据y（n）的最小均方估计，可以将y（n）对应的新息过程定义为［3］：

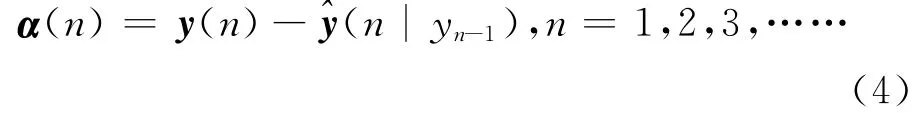
式中：M×1向量α（n）为观测数据y（n）中新的信息。

（2）新息过程的相关矩阵

为了求出新息过程α（n）的相关矩阵，通过递归法求解状态方程（1），可以得到：

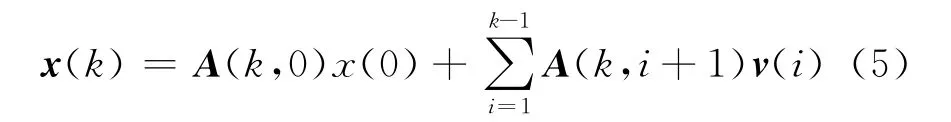
由式（5），可以将新息过程表示如下：

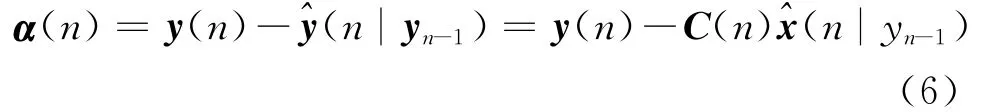
将测量方程式（3）代入式（6），得：

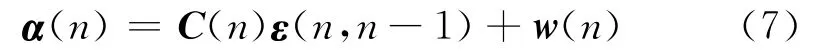
（3）卡尔曼增益

应用新息过程进行状态估计可得：

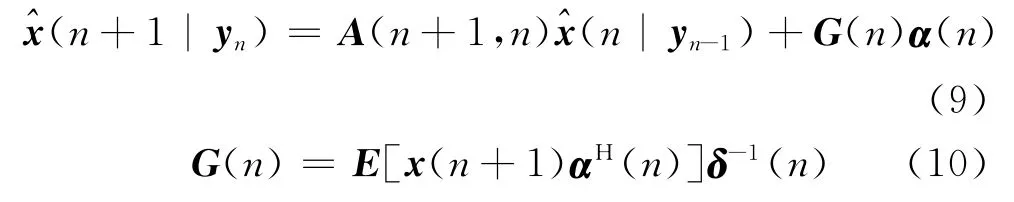
（4）滤波

首先假定过程噪声v（n）和状态向量x（n）相互独立。由状态方程（1）可以得到n＋1时刻状态x（n＋1）的最小均方估计为：

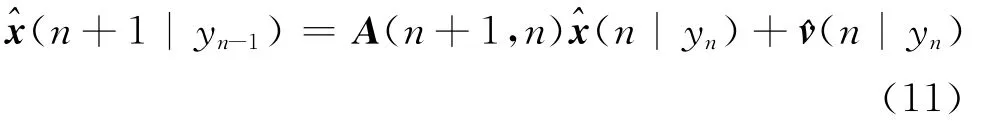
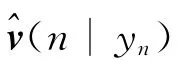
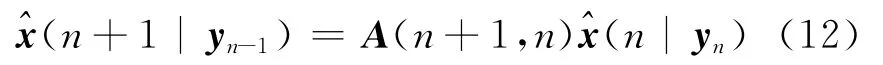
2 仿真分析

航姿参考系统使用的三轴MEMS陀螺和三轴磁阻传感器采用集成电路设计，成本低，可靠性高，环境适应性和适装性较采用模拟分立器件的传统导航设备大为提高。但这些集成器件的采样数据一致性差，包含随机漂移等误差。所以航姿参考系统输出的航向等数据需要使用卡尔曼滤波进行处理，提高数据的准确度，才能满足精度要求。

航姿参考系统输出的航向数据除了受器件噪声影响以外，转动到90°及270°附近时，会连续出现几个相同的数值。这是因为，磁力计的方位角α可以表示为：

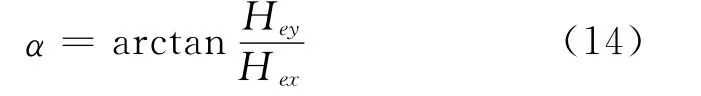
式中：Hey和Hex为地磁场在航姿参考系统的y轴与x轴方向上的分量。

由公式（14）可知，航姿参考系统转到90°或270°时存在奇异点，导致航向数据在特定角度范围内难以分辨出现几个相同的数值。所以卡尔曼滤波不但要解决噪声干扰还要能够解决上述问题。

仿真一：理论数据仿真。

该仿真主要评估卡尔曼滤波对噪声的处理能力。通过对夹杂噪声的正弦曲线的处理，可以评估出滤波效果。图2中，线状曲线是夹杂有高斯噪声的原始数据，点状曲线是通过卡尔曼滤波之后的数据。从图2可以看出，经过滤波后的数据明显得到了很好的改善。

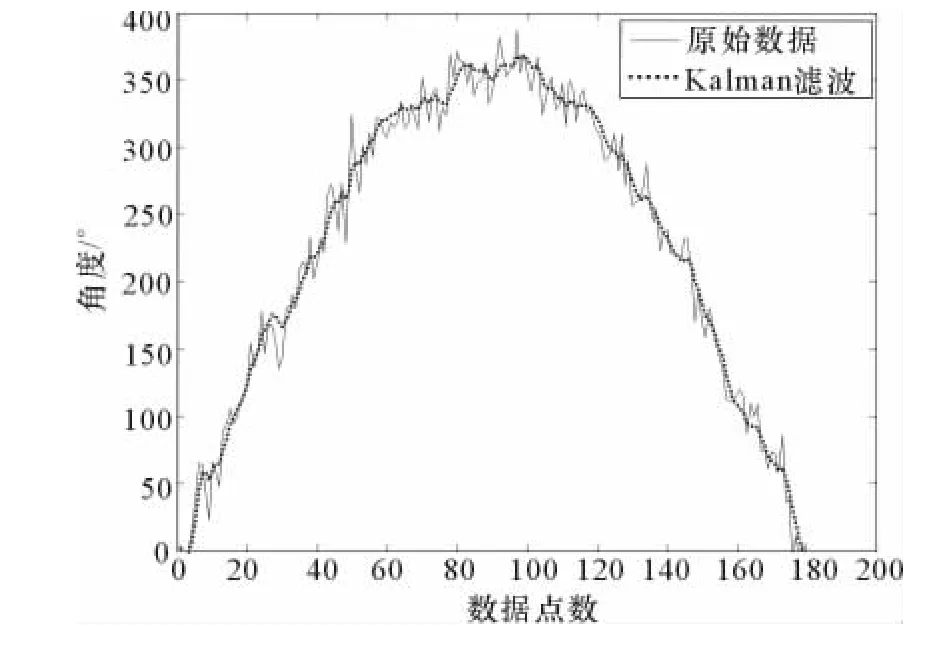
图2 卡尔曼滤波前后的数据波形图

仿真二：对实验数据进行卡尔曼滤波处理的仿真。

该仿真主要评估卡尔曼滤波在实际工作环境下的滤波处理能力。实验条件：将航姿参考系统固定在转台上，转台以30°／s的转速匀速转动，此时可得到航姿参考系统输出的航向角数据。经分析数据后发现，在90°及270°时，数据曲线会出现几个相同的采样值，数据的噪声较大，线性度差，需要对数据进行平滑处理。

图3及图4中，线状曲线代表航姿参考系统在90°及270°附近的真实采样数据，点状曲线代表经过卡尔曼滤波后的数据；从图中可以明显地看到，经滤波后的数据在90°和270°的数据点上得到更好的平滑，线性度明显改善。

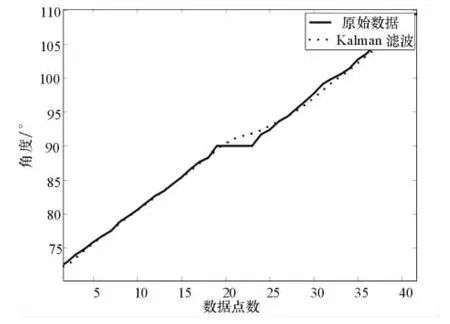
图3 航姿参考系统在90°方位附近数据的滤波效果

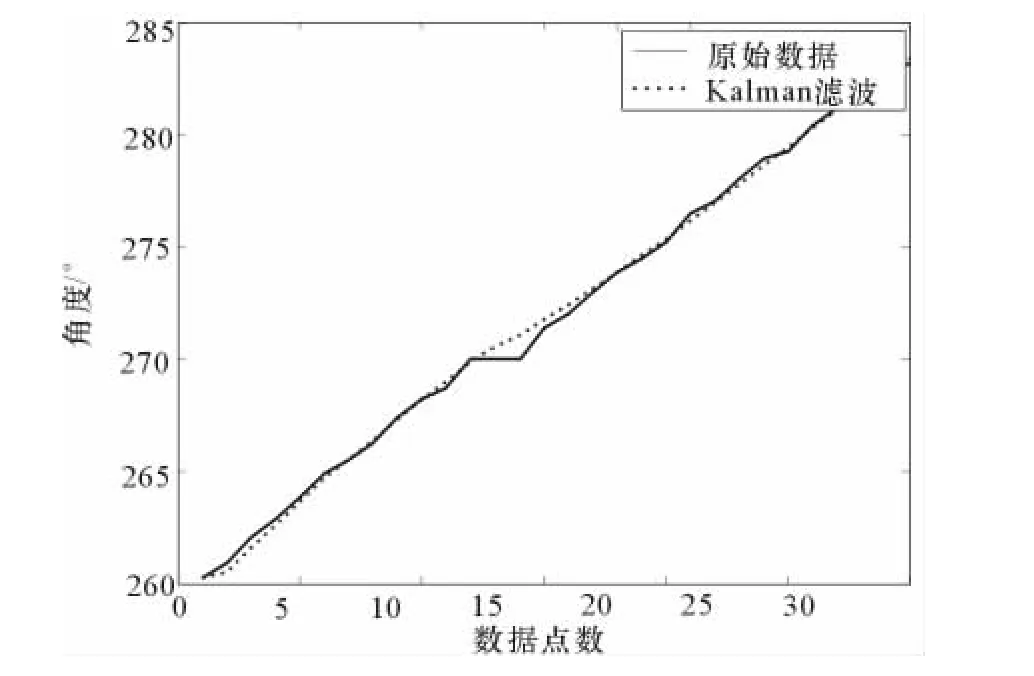
图4 航姿参考系统在270°方位附近数据的滤波效果

3 结束语

卡尔曼滤波算法具有以下明显的优点：

（1）在对随机信号做估计时，卡尔曼滤波是常用的算法之一。由于采用了递推算法，实时测量信息经过提炼被浓缩在估计值中，不必存储所有时刻的测量值，当滤波步数增加时，所提取出的信息浓度也会逐渐增加。

（2）对估计量和测量量的知悉要求低，在已知驱动被估计量的驱动噪声的统计特性以及描述这种驱动作用的系统状态方程和测量噪声的统计特性的情况下，即可进行卡尔曼滤波运算。由于系统的状态方程是准确已知的，测量噪声及驱动噪声为高斯白噪声，且统计特性是不随时间变化的平稳过程，因而对非平稳的被估计量，卡尔曼滤波是一种最优的估计。

本文中的航姿参考系统输出的航向数据经卡尔曼滤波处理后已满足了设计要求。经过处理后的数据去除了奇异点，更加平滑，更接近真实值，输入到设备伺服系统后，显著提高了其闭环控制精度，取得了良好的应用效果。随着计算机信息技术的发展，卡尔曼滤波的处理速度和性能将得到进一步提高，应用将更加广泛。

［1］陆根源.信号检测与参数估计［M］.北京：科学出版社，2004.

［2］孙璐璐，姜洋，王学敏.基于Kalman滤波的机动目标跟踪方法研究［J］.舰船电子对抗，2011，34（3）：32－35.

［3］王华，李有军，刘存建.MATLAB电子仿真与应用教程［M］.北京：国防工业出版社，2007.