基于相位差变化率定位算法的研究

李 帅，钮俊清，田明辉，马 敏

（中国电子科技集团公司38所，合肥230088）

0 引 言

对于非合作辐射源的单站无源定位技术在电子对抗、侦察、监视等领域具有重要地位，受到广泛关注［1］。传统的单站无源定位体制是依靠单个运动观测平台在不同时刻测量到达角进行交叉定位［2］，其定位收敛时间长，定位精度不够精确。

无源定位技术正朝着高精度、高速度的方向发展，主要依赖于参数测量和处理能力的提高［3－4］。现阶段，相位差变化率定位算法［5－6］是依据运动学原理，提取辐射源目标和观测平台的相对运动信息进行定位，定位速度和精度都有了一定程度的提高，在现代战争中具有广阔的应用前景。

本文结合工程使用并借助卫星工具开发包（STK）软件对基于相位差变化率的定位算法进行了详细的仿真实验，研究定位算法中不同参量对定位结果的影响。

1 定位算法

1.1 基于相位差变化率的单站定位算法原理

设载机飞行速度是VA，雷达位于固定位置P，雷达与载机处于同一个平面，到达角是θ，机动单站无源定位的动力学原理如图1所示。

当载机沿着图1所示航线飞行时，载机与雷达之间的视线将按照角速度旋转，即：VAsinθ＝R·，由此可得：

推导可得载机与雷达之间距离为：

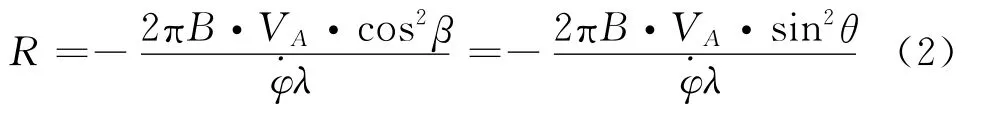
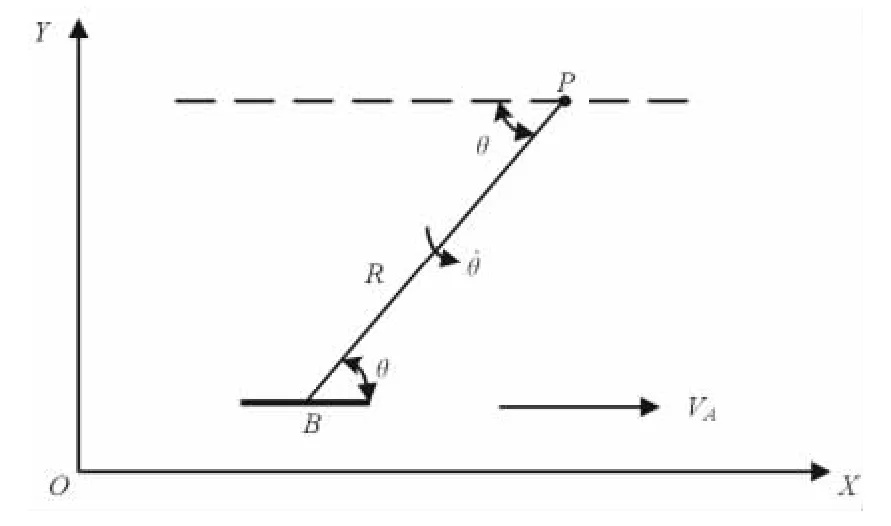
图1 机动单站无源定位的动力学原理

式中：λ为信号波长；θ为雷达的方位角；φ·为信号相位差变化率；B为干涉仪基线长度。

再利用雷达的方位角θ，雷达的位置可以表示为：

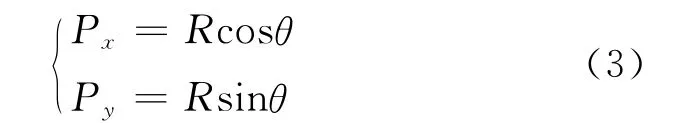
通过以上的分析可知，通过测量飞机直线运动引起的相位变化率可以获得目标距离R，再结合雷达的到达角θ，即可确定雷达的位置（Px、Py）。

该算法的输入参数包括测向、相位差变化率、目标频率及对应的基线长度。现阶段测向误差和相位差变化率误差是无法避免的，并且定位结果对其敏感。为了提高最终的目标定位速度和精度，采用以下方式进行优化解决：

（1）提高测量数据率；

（2）对高数据率的测向和相位差变化率进行卡尔曼滤波算法处理，降低随机误差的引入；

（3）对定位结果进行扩展卡尔曼滤波算法（EKF）［5］处理，提高定位速度和精度。

1.2 滤波算法

在实际算法应用中，由于不可避免的测量误差，必须使用合适的滤波算法来收敛定位结果，本文选用EKF滤波算法进行定位结果滤波。

通常EKF采用的线性化方法是将非线性状态方程按泰勒级数展开。

探测目标微分方程为连续状态方程，记为：

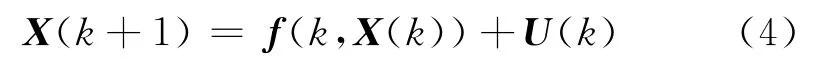
量测方程：

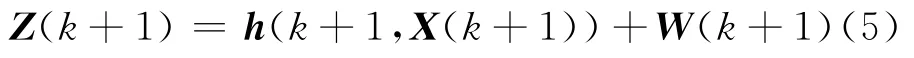
式中：U（k）为过程噪声；W（k＋1）为量测噪声；两者均为高斯零均值噪声。

泰勒级数的展开式只保留一阶项，即可得到一阶扩展卡尔曼滤波的状态方程：

式中：fX（k）为雅各比矩阵。

状态的一步预测：

协方差的一步预测：

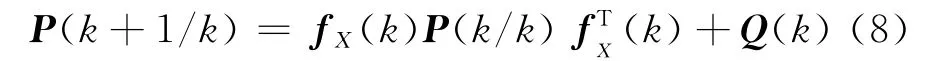
式中：Q（k）为过程噪声协方差。

量测预测值：

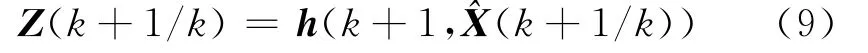
相伴的协方差：

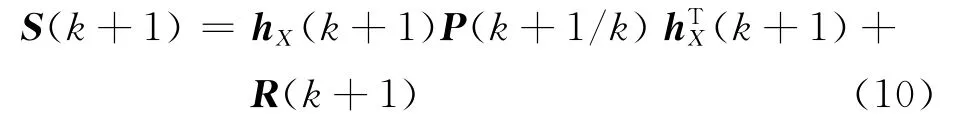
式中：hX（k＋1）为雅各比矩阵；R（k＋1）为量测噪声协方差。

增益矩阵：

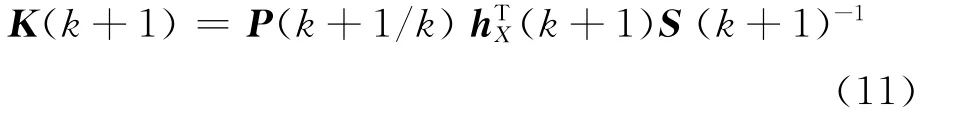
状态更新方程：

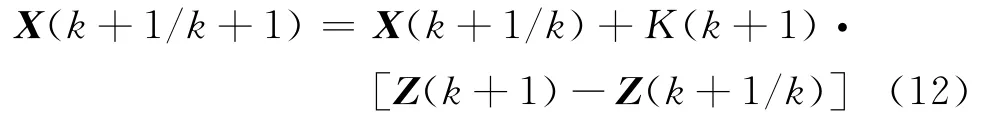
协方差更新方程：

式中：I为与协方差同维的单位矩阵。

EKF在应用于非线性不强的问题上具有不错的性能，同时其计算复杂度不高，总体上看其费效比较高。

1.3 定位算法流程

基于相位差变化率的辐射源定位流程如图2所示。对于数据处理分系统的输入（测向信息、相位差信息），在其进行定位结算之前进行二维卡尔曼滤波，减少随机误差对测量值的影响，提高定位结算的精度；结合测向滤波值、相位差变化率滤波值进行定位结算，并对定位结算结果再次进行EKF滤波，进一步提高定位解算精度；最后，通过坐标变换，可得定位目标的经纬度。

2 仿真实验

仿真实验借助STK软件，进行了仿真实验参数的设置，包括机载平台的速度、高度、目标截距等，同时在仿真时也引入了工程中需要考虑的测向测量误差、航向角误差等。仿真实验包括以下4个方面：

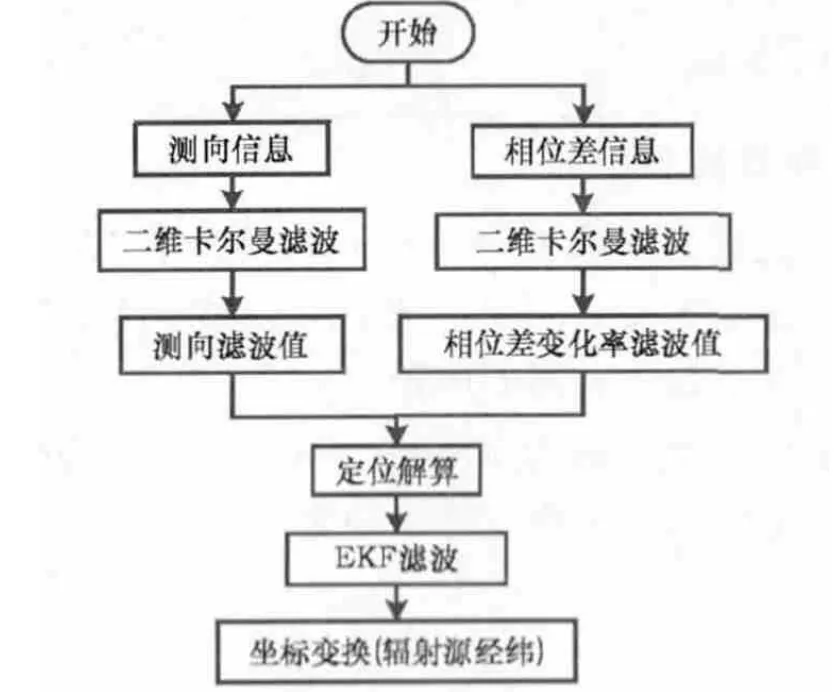
图2 基于相位差变化率定位算法流程

（1）相同的仿真实验参数和仿真场景，研究测向精度对定位结果的影响；

（2）相同的仿真实验参数和仿真场景，研究相位差变化率对定位结果的影响；

（3）相同的仿真实验参数和仿真场景，研究目标频率对定位结果的影响；

（4）相同的仿真实验参数和仿真场景，研究截距对定位结果的影响。

针对上面所述的4个方面，对应以下的4个仿真实验，通过计算给出定位结果，并分析总结不同参数对本文算法定位结果的影响。

2.1 仿真实验1

在其他仿真实验参数相同的情况下，研究目标探测方位角精度不同对本文算法定位结果的影响。方位精度分别为1.0°、1.6°、2.2°、2.8°，测向精度对定位结果的影响如图3所示，不同测向精度对应的定位结果如表1所示。

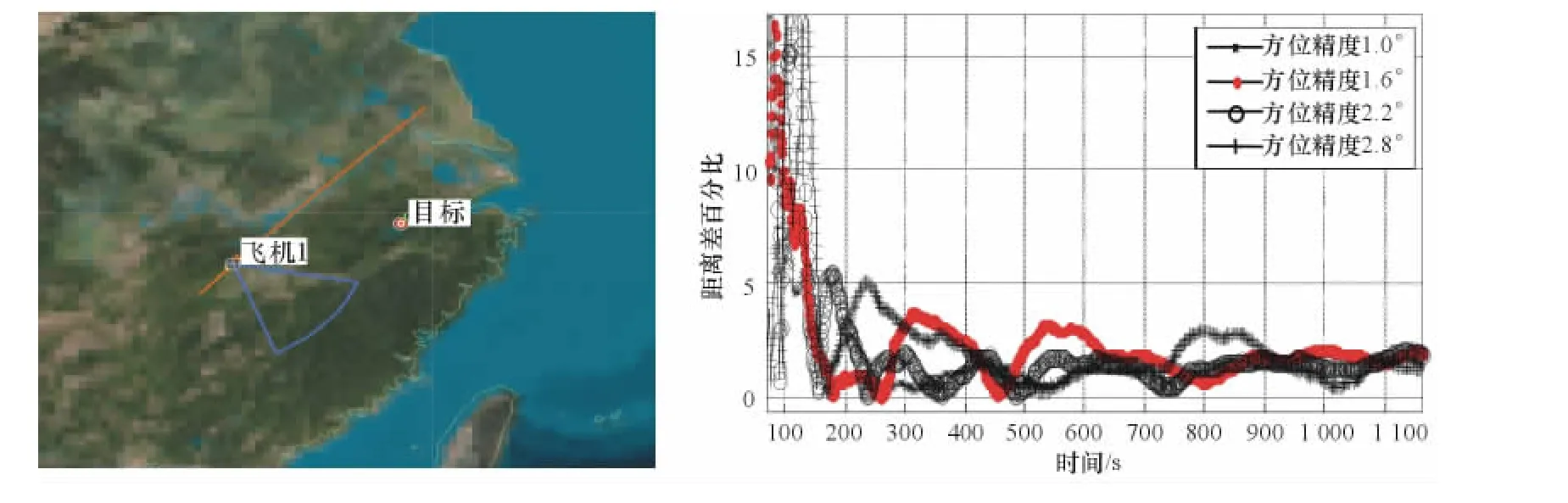
图3 测向精度对定位结果的影响

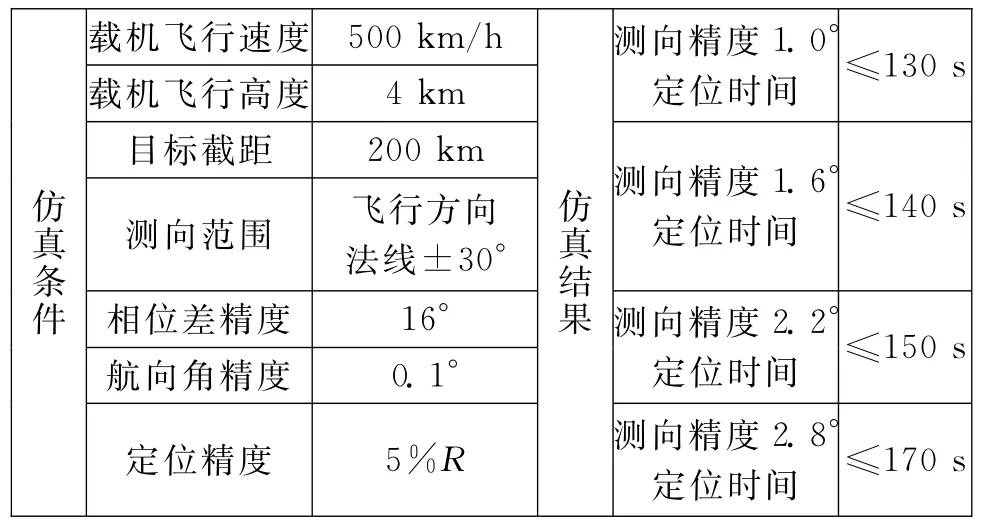
表1 不同测向精度对应的定位结果

2.2 仿真实验2

在其他仿真实验参数相同的情况下，研究不同目标探测相位差精度对本文算法定位结果的影响。相位差精度分别为10°、14°、18°、22°，相位差精度对定位结果的影响如图4所示，不同相位差精度对应的定位结果如表2所示。

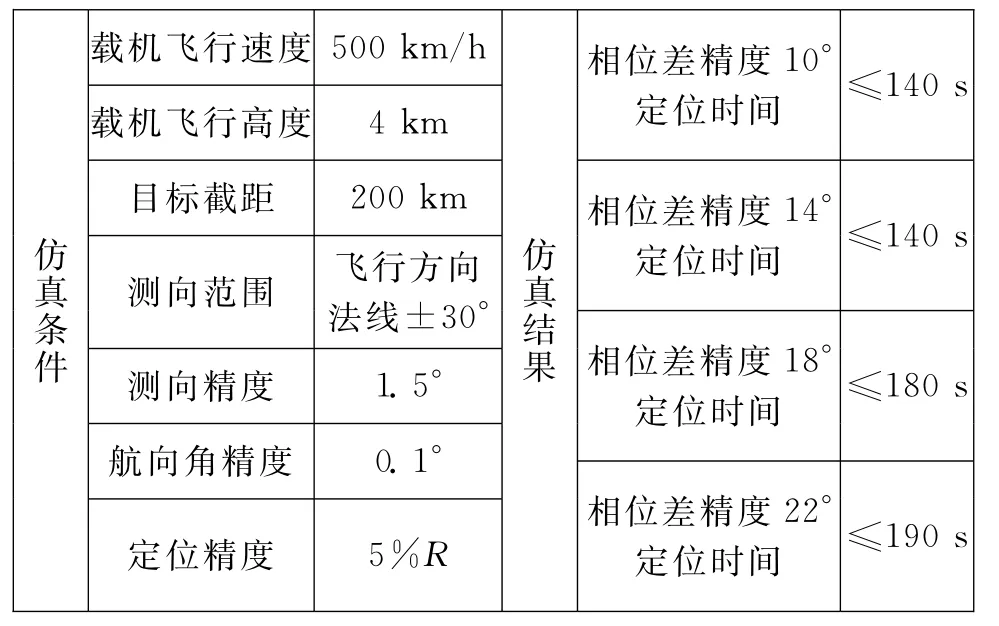
表2 不同相位差精度对应的定位结果

2.3 仿真实验3

在其他仿真实验参数相同的情况下，研究不同探测目标频率对本文算法定位结果的影响。目标频率对定位结果的影响如图5所示。目标频率及基线长度参数对照如表3所示。

图4 相位差精度对定位结果的影响

表3 目标频率及基线长度参数

2.4 仿真实验4

在其他仿真实验参数相同的情况下，研究不同目标截距对本文算法定位结果的影响。目标截距对定位结果的影响如图6所示。

目标截距分别为100km、150km、200km。不同目标截距对应的定位结果如表4所示。

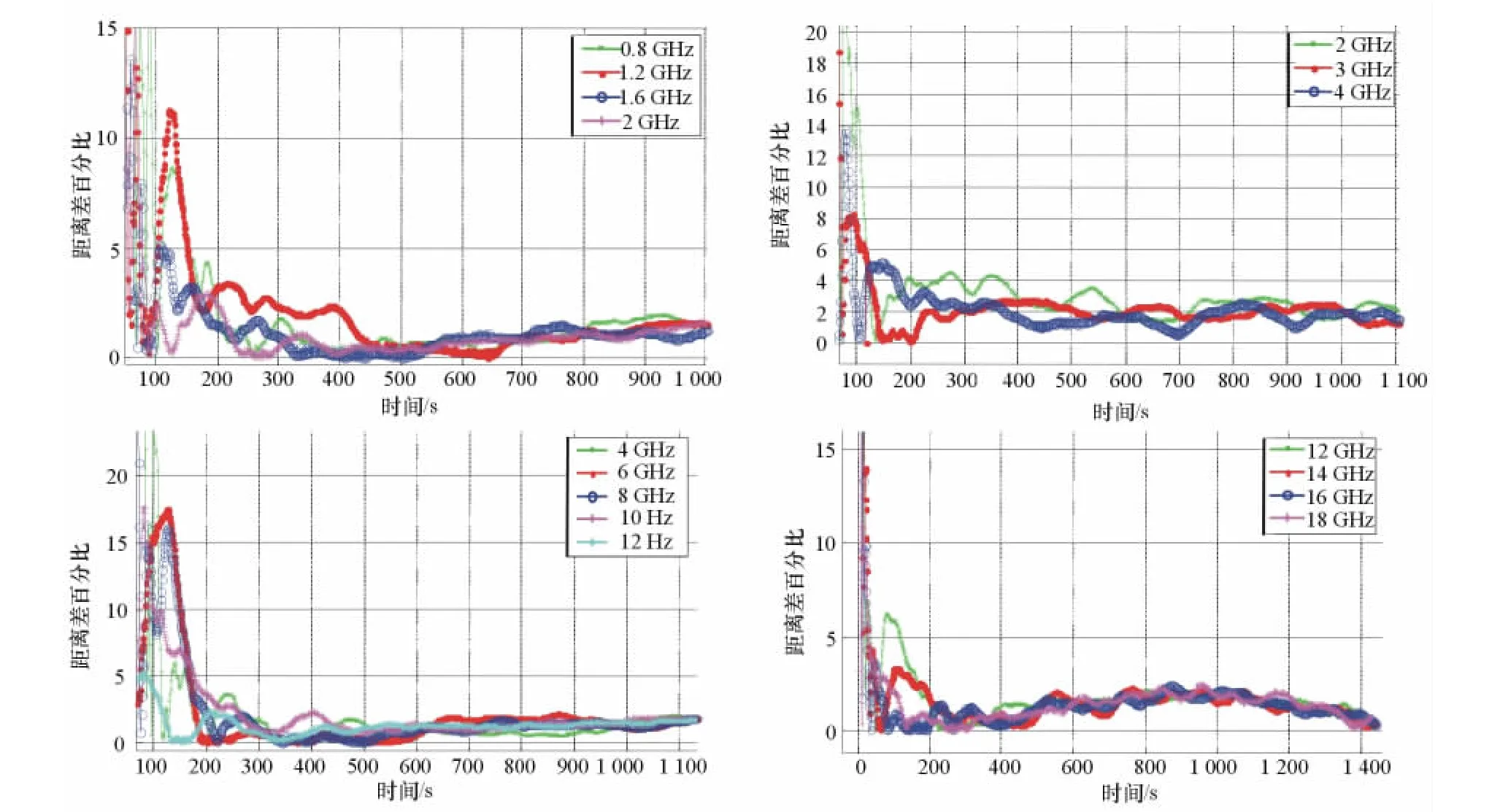
图5 目标频率对定位结果的影响

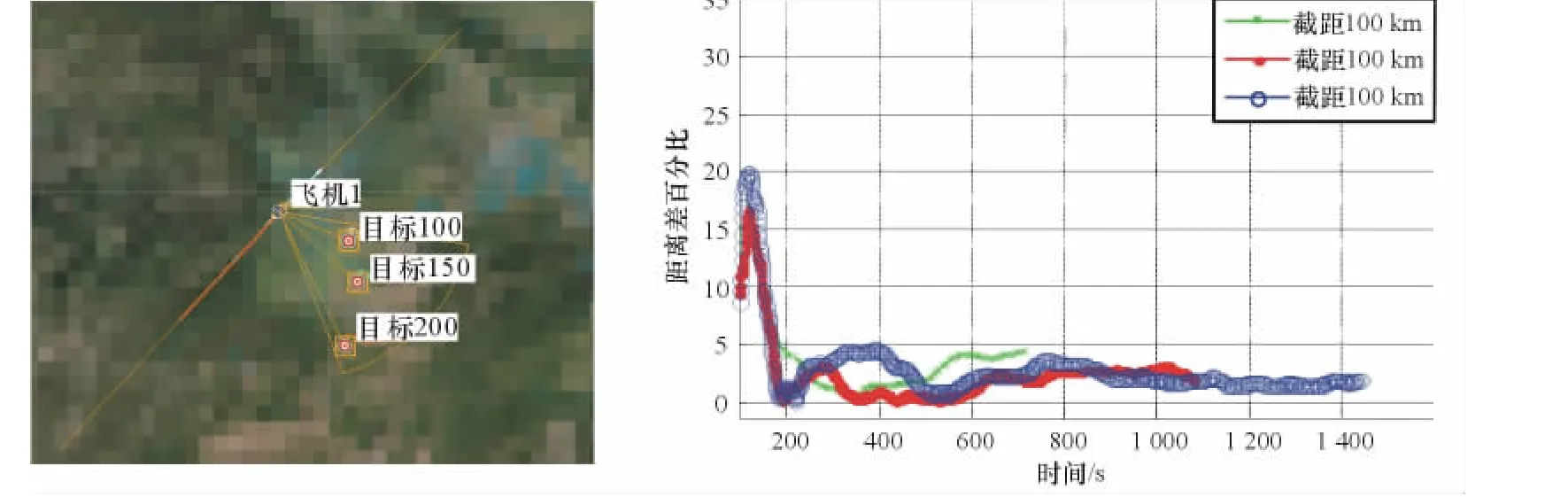
图6 目标截距对定位结果的影响

从仿真实验结果可知：随着测向精度的增加，定位时长也在逐渐增加；随着相位差精度的增加，定位时长也在逐渐增加；随着目标频率的增加，定位时长相对比较稳定，但仍有减少的趋势；随着目标截距的增加，定位时长相对稳定。

表4 不同目标截距对应的定位结果

3 结束语

综上所述，基于相位差变化率定位算法引入了卡尔曼滤波和扩展卡尔曼滤波，通过仿真实验，验证了该算法的可行性和鲁棒性。在同等的定位精度要求下，随着测向精度和相位差精度的逐渐增加，定位时长逐渐增加，但仍在工程应用可以接受范围之内。

随着目标频率的增加，定位时长在保持稳定的基础上有减少的趋势，而目标截距对定位时长影响不大。总的来说，基于相位差变化率定位算法具有很强的实用性，可以满足实际工程应用快速精确定位的需要。

［1］孙仲康.基于运动学原理的无源定位技术［J］.制导与引信，2001，22（1）：40－44.

［2］姚坤，陈天麒，李立萍.单站无源定位跟踪方法研究［D］.成都：电子科技大学，2003.

［3］许耀伟，孙仲康.利用相位差变化率对固定辐射源的无源被动定位.系统工程与电子技术，1999，21（3）：34－37.

［4］Xi W，Yu B Z，Wang S S.Theoretical analysis of direct finding targets with rolling－airframe passive radar by phase interference technique［A］.Proceedings of International Conference on Radar［C］，2006：1－4.

［5］程咏梅，潘泉，张洪才，等.基于扩展卡尔曼滤波的多站被动式融合跟踪［J］.系统仿真学报，2003，15（4）：548－550.

［6］张国毅，宋德亮，陈枫.PRI变化雷达信号相位差变化率定位法研究［J］.舰船电子对抗，2010，33（3）：35－38.