基于盲源分离的雷达信号分选方法
2013-10-13陆志宏盛骥松吴宝东
杨 康,李 迪,陆志宏,盛骥松,吴宝东
(船舶重工集团公司723所,扬州225001)
0 引 言
在现代电子战复杂的电磁环境下,存在大量的雷达电磁信号,雷达侦察接收机在对实际侦收到的雷达信号进行处理的过程中,由于雷达信号调制样式具有多样性,雷达信号是如何混合在一起无从知道,再加上传统的信号分选算法建立在脉冲描述字(PDW)参数分析基础上[1-4];因此,雷达侦察设备对同频或频谱混叠的雷达信号可能无法分选。
盲信号处理的提出正好解决了这方面的困难,盲源分离方法的实质是在源信号和传输信道未知的情况下,利用接收天线的输出,恢复并统计独立源信号的过程。
尽管相继出现了许多盲信号分离算法,但是这些算法大都是应用在语音识别、生物医学工程和图像信号处理等方面,在侦察雷达信号处理方面的应用较少[5]。
为此本文给出了复杂电磁环境下基于最大信噪比的盲分离算法,将其运用到对侦收到的雷达信号进行分离当中,并通过计算机的仿真证实了这种方法的可行性和有效性。
1 信号阵列接收模型
信号阵列接收模型如图1所示。
观测数据可用如下数学模型来描述:

式中:Xt= [X1t,…,Xmt]T,为 m 维的观测信号向量,其元素是各个天线的输出;St= [S1t,…,Snt]T,为n维的源信号向量;nt= [n1t,…,nmt]T,为m维的加性噪声向量;A= [a1,…,an],为m×n维的混合系数矩阵,其元素表示信号的混合值。
盲信号分离的目的在于在没有信号先验知识的情况下,统计和恢复源信号矩阵。又因为本文旨在验证盲信号分离对雷达信号分选的可行性,因此,为简化计算,忽略噪声的影响(即原信号与观测信号之间存在线性关系),进而有:
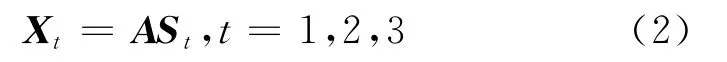
式(2)是一种线性瞬时混合模型,其物理意义是:未知的n个源信号通过未知形式的混合后通过m个输出端得到m维观测数据矩阵。
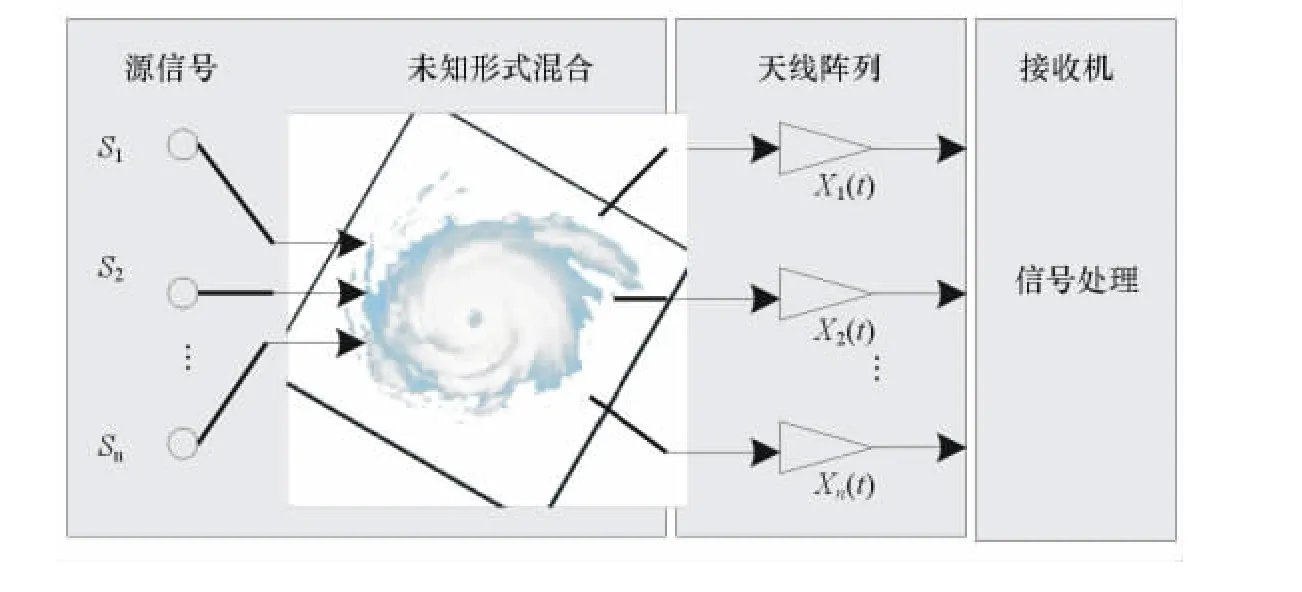
图1 信号阵列接收示意图
由盲信号分离的原理可知:只根据观测信号矩阵Xt,若能确定存在1个线性变换W,使得Yt=WXt,那么Yt即是对源信号St的估计矩阵,W 也称为分离矩阵。
2 基本假设
为了使雷达源信号可分,源信号矩阵和接收到的混合矩阵满足一定的约束条件:
(1)各雷达发出的信号相互独立;
(2)各雷达信号的形式中最多只能包含1个高斯信号;
(3)接收到的混合矩阵A包含足够的混合信息,为列满秩矩阵(m>n)。
3 信号盲分离原理
根据公式(3),求解分离矩阵W,使其作用于观测信号矩阵Xt,使系统输出矩阵Yt=WXt是源信号矩阵St的估计。能够求解分离矩阵W 的算法很多,但其求解步骤基本相似,可表示如下:
(1)构造准则函数(也称为目标函数),即构造分离矩阵W的目标函数。
(2)对目标函数求极值。可利用某种算法来搜索目标函数的极值点,当目标函数出现极值点时,对应W的最优解。
4 基于最大化负熵的FastlCA盲分离算法
4.1 数据预处理
在实际接收过程中,各个天线阵元接收到的信号存在冗余;因此,在信号盲分离处理之前,首先应对观测到的数据进行预处理。具体方法见文献[6]~[7]。预处理的结果是使每个输出端观测的数据彼此间不相关(即白化后数据各分量互相正交且方差都等于1),假设观测数据矩阵X已去除均值,寻求1个预处理矩阵V,使得变换后的输出Z=VX不相关,即:
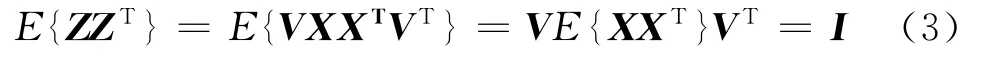
关于预处理矩阵V 的求解在文献[6]~[7]中已有阐明,在此不再赘述。
4.2 以负熵最大化目标函数作为准则函数
设W为分离矩阵,w为W 的1列向量,X是已经过预处理后的数据,将负熵最大化目标函数代入Yi=wTX得:

在约束E[(wTX)2]=‖w‖2=1下,构造代价函数如下:
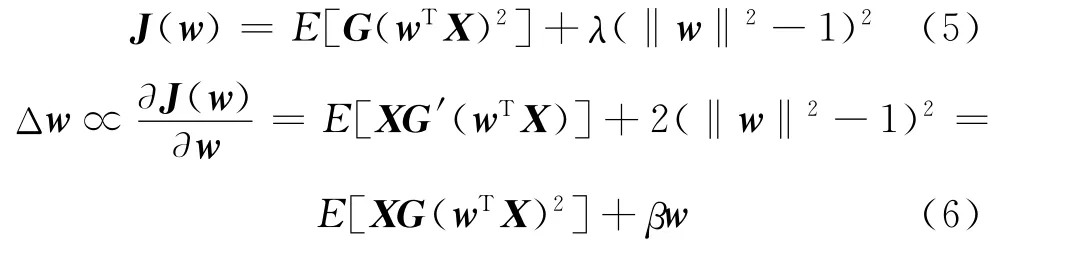
稳态时,Δw=0,即:
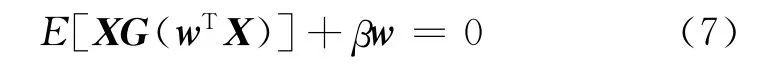
4.3 以牛顿迭代算法进行优化
用牛顿迭代算法,迭代式为:
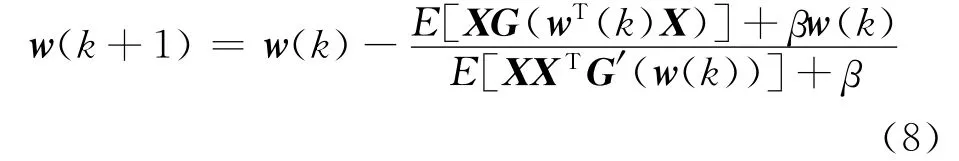
上式两边乘以E[XXTG′(w(k)T)]+β,经过代数化简得到下述固定点算法:
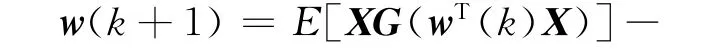
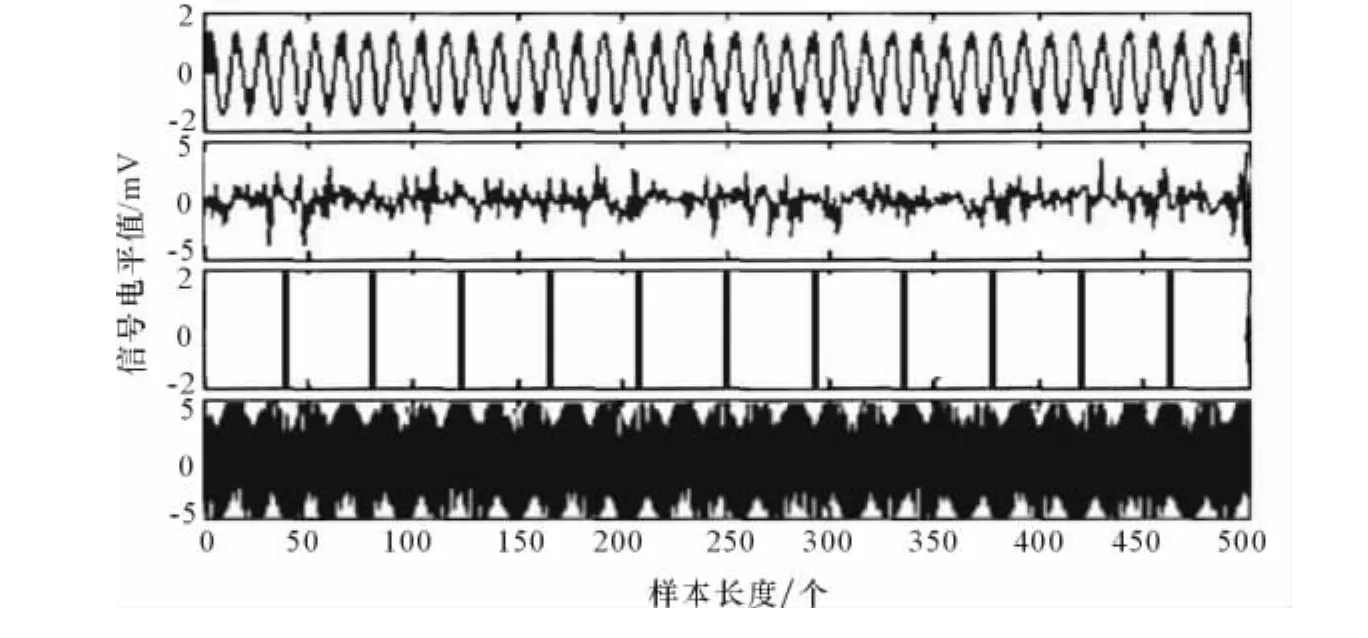
图2 模拟的源信号
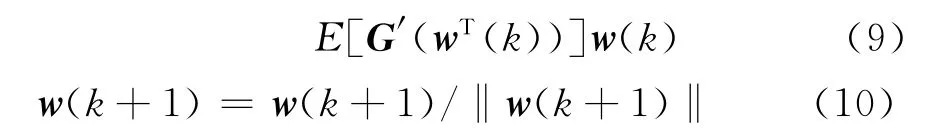
5 仿真实验与分析
为验证上述算法的有效性和可行性,用Matlab工具箱模拟了4部雷达源信号,用上述算法对混合后的信号进行了分离。采样样本数量5 000,显示波形的样本数量500。源信号分别为正弦信号、脉冲噪声、方波信号、余弦叠加信号,其波形如图2所示。
混合矩阵A为均匀分布的随机矩阵:

图3是原信号与随机矩阵混合后的信号波形。用上述算法更新分离矩阵W,并提取各个源信号。FastICA算法的恢复信号波形如图4所示,通过FastlCA算法计算得到的分离后矩阵Y和分离矩阵
为了评价算法的性能,本文引入相似系数pij作为判定标准,其定义如下:
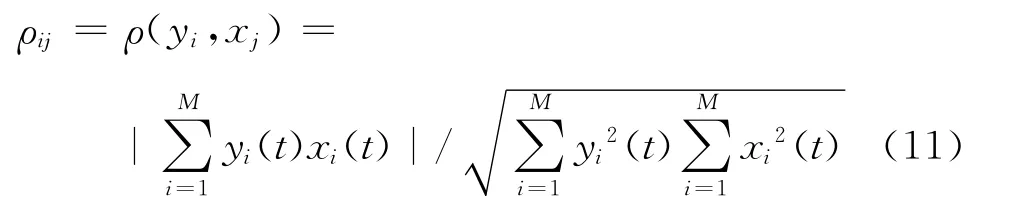
ρij的值域为:0<ρij<1,越接近1表明分离后的信号与原信号越相似,算法效果越好;越接近于0时表明分离后的信号与原信号越不相关,算法效果越差[8-10]。
从表1可以看出,此算法分离后的信号和源信号的相似系数都接近值域上限,表明算法效果较好,可以把分离后的信号作为源信号的近似估计。尽管w分别为:

分离后的信号与源信号相比在幅度和次序上发生了变化,但波形没有变化,因此不影响对信息的分析。
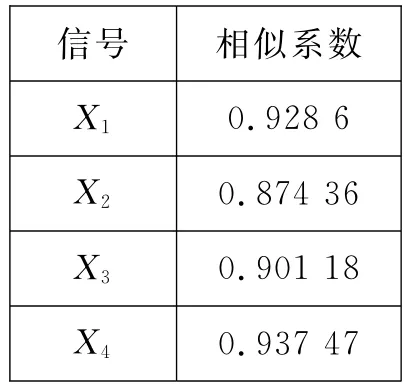
表1 相似系数表
6 结束语
本文依据盲源分离原理,通过仿真,利用天线阵列接收到的信号输出,在无先验知识的情况下,运用基于最大化负墒的FastICA算法,求解雷达源信号与接收观测数据间的分离矩阵,对雷达信号实现了盲分离,证明了此算法的有效性和可行性。下一步的工作将研究算法在有噪模型下的去噪性能。
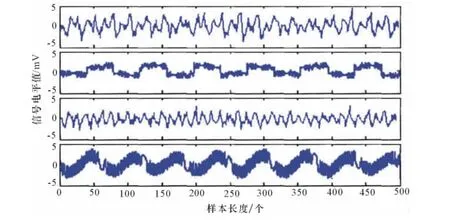
图3 混合后的信号
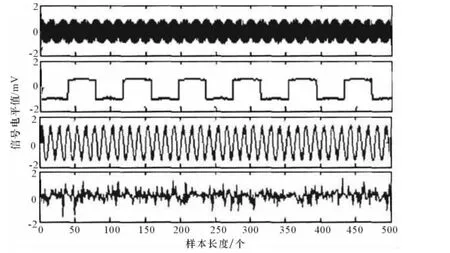
图4 分离后的信号
[1]张葛祥,胡来招,金炜东.基于熵特征的雷达辐射源信号识别[J].电波科学学报,2005,20(4):440-445.
[2]Common P.Blind separation of source,PartⅡ:Problems statement[J].Signal Processing,1991,24(2):11-20.
[3]Sorouchyari E.Blind separation of sources,PartⅢ:stability analysis[J].Signal Processing,1991,24(l):21-30.
[4]Cichocki A,Moszczynski L.A new learning algorithm for blind separation of sources[J].Electronics Letters,1992,28(21):1986-1987.
[5]Hyvarinen A.Fast and robust fixed-point algorithms for independent component analysis[J].IEEE Transactions on Neural Networks,1999,10(3):626-634.
[6]Cheung Y M,Liu H L.A new approach to blind source separation with global optimal property[A].Proceedings of The IASTED International Conference of Neural Networks and Computational Intelligence[C].Grindelwald,Switzerland,2004:137-141.
[7]史习智.盲信号处理——理论与实践[M].上海:上海交通大学出版社,2008.
[8]王振力,刘志华,白志强.基于卷积盲源分离的噪声鲁棒性语音识别的研究[J].声学技术,2009,28(3):276-278.
[9]王晓燕,韩俊宇,楼顺天.基于盲源分离技术的雷达信号分选研究[J].电子对抗,2005(5):29-32.
[10]裴学广.基于变步长自然剃度算法的盲源分离[J].舰船电子对抗,2007,30(4):65-68.
