换热网络的热流均匀性因子
2013-10-11万义群崔国民方大俊彭富裕
万义群,崔国民,方大俊,彭富裕
(上海理工大学新能源科学与工程研究所,上海 200093)
换热网络的综合及优化是实现能量综合利用的重要环节,其在节能和降低产品成本方面有着非常重要的意义。迄今国内外已开发出许多针对换热网络的优化综合方法,这些方法基本可以分为夹点技术法[1-2]、数学规划法[3]和启发式方法[4-6]三大类。
换热网络的优化过程中常用的目标函数是换热网络的年综合费用,但从优化的结果来看,换热网络的综合费用并不是完全与换热效能相一致的,这是由于以综合费用为目标的优化方法并没有从提高总体换热效能的角度出发,获得的换热网络只是在综合费用上达到一定程度的最优。从本质上讲,提高换热网络的换热效能是解决换热网络优化问题的最根本途径,因为换热效能的提高能够使得能量得到有效地综合利用,如果要获得更优的换热网络结构,必须从换热效能的角度为换热网络提出新的评价指标及新的优化思路,从根本上改进换热网络结构。
过增元院士等[7-8]从换热器沿程温差与换热效能的关系出发,提出了两股流换热器的温差均匀性优化原则,依据该原则对换热器进行改进能够提高换热器的换热效能;文献[9]将温差均匀性优化原则应用在多股流换热器上,建立了多股流换热器设计的温差均匀性因子,能够用于衡量多股流换热器通道排列的优劣,从而能指导多股流换热器的优化设计;文献[10-12]从换热网络整体强化的角度出发提出了换热网络的温差均匀性优化原则,建立了换热网络的温差均匀性因子,试图为换热网络的换热效能提供一种新的评价指标,并能指导换热网络的优化设计。
从场协同理论[13-14]的角度来看,将换热器沿程的对流换热系数以及换热器的固壁导热系数、固壁均匀程度都考虑进来,那么换热器的热流边界条件越均匀则其换热效能就越高[15-16];而换热网络是一个多流体,多物性的复杂换热流场,因此换热网络的温差均匀性因子并不能作为换热效能绝对的评价指标。如果将各流体的换热系数都考虑进来从而建立换热网络的热流均匀性因子,则其将更适合于作为换热网络效能的评价指标。
鉴于此,本文在换热器网络的温差均匀性因子及场协同理论的基础上,提出并建立换热网络的热流均匀性因子,着重验证及分析换热网络整体换热量与热流均匀性因子之间的关系,试图从能量有效利用的角度为换热网络的换热效能建立新的评价指标,并为换热器网络的综合及优化提供新的方法和思路。
1 换热网络热流均匀性因子的建立
1.1 换热网络的温差均匀性因子
文献[11]从换热网络的换热效能出发,提出了换热网络温差均匀性因子的概念,并通过对换热网络温差场的分析,建立了基于换热网络离散温差场的温差均匀性因子,其建立的温差均匀性因子表达式如式(1)。
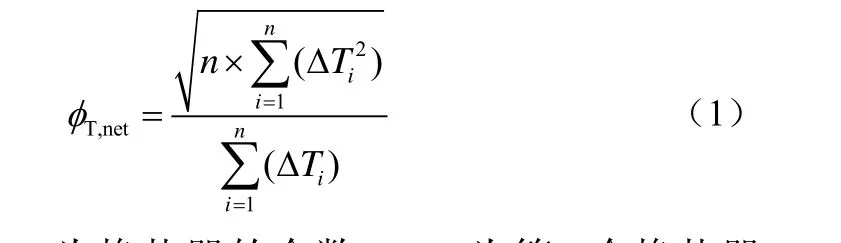
式中,n为换热器的个数;ΔTi为第i个换热器的对数平均温差。
通过具体的实例分析表明[11]:换热网络温差均匀性因子φT越小,则整个换热网络的温差场越均匀,换热效能越高。但该表达式没有将换热网络中各流体的换热系数考虑进来,在实际工程中所面对的换热网络优化问题总是包含不同换热系数的流体,对于多流体,多物性的换热网络复杂流场,温差均匀性因子的适用性受到了很大的限制,因此本研究将建立更适合于评价换热效能的换热网络的热流均匀性因子。
1.2 换热网络的热流均匀性因子
根据对流换热过程的场协同理论,恒壁温的边界条件将抑制对流换热,而恒热流的换热边界条件,将最大限度地发挥对流换热的作用,据此建立了换热器热流均匀性因子的概念[15],将换热器沿轴向划分为N个微元换热体,每个微元的热流密度为qi(i=1,2,··,N),则单体换热器的热流均匀性因子φq,s可表示为式(2)。

式中,N为单个换热器的微元体个数;qi为第i个微元体的热流密度。
本研究借鉴单体换热器的热流均匀性因子表达式,将复杂换热网络中每个换热器作为一个换热单元体划分为n个单元,建立换热网络的热流均匀性因子φq,net,表达式如式(3)、式(4)。
综上所述,胎心监护、脐动脉血流联合血清HIF-1α水平检测对胎儿窘迫的诊断有重要的临床价值,其指标表达异常可直接关乎新生儿的结局,临床对于临产的孕妇应建议进行联合检测,尽早发现是否出现胎儿窘迫,积极采取有效措施,将新生儿伤害风险降至最低。
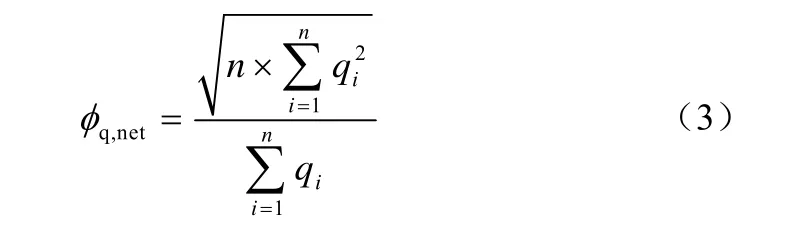

式中,n为换热器的个数;Qi、Ai、qi分别为第i个换热器的换热量、换热面积和热流密度。
考虑到换热网络中单个换热器的换热量均不相同,其对热流均匀性因子的影响及贡献不同,如果所有的换热器都按相同的权重计算,那么就很难准确反映出这一网络的换热特点,因此通过加权的方式增加换热能力强的换热器在热流均匀性因子中的作用。计算各换热器的换热量Qi(i=1,2,··,n),取其中的最小值Qmin=min{Q1,Q2,··,Qn},将各换热器的换热量与Qmin的比值mi作为各换热器的权重值,则热流均匀性因子按换热量加权的计算公式为式(5)、式(6)。
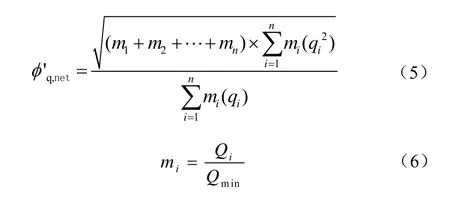
式中,n为换热器的个数;Qi、mi、qi分别为第i个换热器的换热量、权重值和热流密度。
本研究最终建立的换热网络的热流均匀性因子φ'q,net表征的是一个换热网络内部热流均匀性的程度。从式(5)可以看出,热流均匀性因子越接近1则换热网络内部热流密度越均匀,其换热性能也越好;该因子能否和换热网络的总换热量之间形成对应关系,能否作为换热网络换热效能的评价指标,需要通过具体的实例进行验证及分析。
2 热流均匀性因子的实例验证及分析
2.1 算例一
算例一采用15股流换热器网络[17-20]来检验并分析换热网络中的热流均匀性因子与换热性能的关系,该换热网络由8股热流体和7股冷流体组成,流股的初始参数见表1,文献[19]中优化的结构如图1所示,图中用两个“●”及其相连的竖直短线表示换热器单元,单个“●”表示公用工程换热单元。本研究将在保持换热单元总面积相同的条件下与在改变换热网络结构的条件下验证分析换热网络的换热性能和热流均匀性因子之间的关系,其中换热性能以换热网络总体换热量的大小作为衡量指标(不包括冷热公用工程的热负荷)。

表1 算例1的流体参数
2.1.1 保持换热单元总面积相同条件下的热流均匀性因子
采用图1所示的换热网络结构,随机改变各换热器单元的面积,计算30组热流均匀性因子,规定保持换热面积的总和等于3000 m2,以此来考察整个换热网络的换热量与热流均匀性因子之间的关系。将换热器面积的总和保持不变则可以削弱换热器面积大小对整个网络换热性能的影响,在这种情况下考察的换热网络热流均匀性因子更具有参考价值。
热流体数目为NH=8,冷流体数目为NC=7,换热网络的级数为NK=2,随机获取换热器单元面积并进行模拟计算,必须满足如式(7)~式(9)的约束条件。
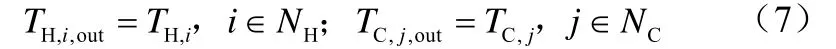
式中,TH,i,out、TC,j,out分别为热流体和冷流体的出口温度;TH,i、TC,j分别为热流体和冷流体的目标温度。
换热单元面积约束:

式中,ACU,i、AHU,j和Ai,j,k分别为冷公用工程单元、热公用工程单元和换热器单元的面积。
换热单元换热量约束:
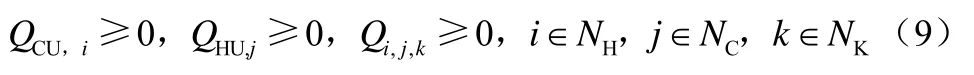
式中,QCU,i、QHU,j和Qi,j,k分别为冷公用工程单元、热公用工程单元和换热器单元的换热量。
首先考察总换热量与是否考虑换热器权重得到的热流均匀性因子之间的关系,所得结果如图2所示,图中φq,net为采用式(3)没有考虑加权求出的热流均匀性因子,而φ'q,net为式(5)考虑换热量权重求得的热流均匀性因子,Q为换热网络的总换热量。从图2中可以看出,总体上热流均匀性因子能与总换热量之间形成较好的对应关系:热流均匀性因子越小,则对应的整个换热网络的换热量越大,即换热网络换热性能越好。比较图中φq,net与φ'q,net可以看出,φ'q,net与Q之间形成的对应关系更好,由此可以说明考虑各换热器换热量的权重计算得到的热流均匀性因子能更准确地反映出换热网络的换热性能。
其次考察总换热量与热流均匀性因子和温差均匀性因子之间的对应关系,所得结果如图3所示。图中φ'q,net为热流均匀性因子,φT,net为温差均匀性因子,Q为换热网络的总换热量。从图3中可以看出,两个因子总体上都能与换热网络的总换热量之间形成较好的对应关系,而热流均匀性因子与总换热量之间形成的对应关系比温差均匀性因子更佳,也就是说对于本文所取的各股流体换热系数不同的换热网络来说,热流均匀性因子更具适用性,能够更准确地反映出换热网络的换热性能。
2.1.2 改变换热网络结构条件下的热流均匀性因子

图2 换热量与φq,net和φ'q,net的关系图

图3 换热量与φ'q,net和φT,net的关系图
上述内容只是在同一个结构中对热流均匀性因子进行讨论,而换热网络的综合及优化总是针对不同的网络结构,不同结构的换热网络总换热量与本研究建立的热流均匀性因子之间是否能形成较好的对应直接关系到热流均匀性因子能否作为换热网络换热效能的评价指标及能否指导换热网络的综合及优化等关键问题。本研究在图1所示的结构基础上随机改变各换热器的冷、热流体匹配,规定每股流体上至多匹配3个换热器,同一位置至多匹配一个换热器,以此取得30个不同的换热网络结构,然后采用牛顿法对每个结构进行优化,目前换热网络的优化都以年综合费用为目标,所以本研究以换热网络年综合费用F为目标函数,换热器单元面积A为变量,从而获得30个换热网络的优化结构。约束条件如式(7)~式(9),目标函数包括投资费用和公用工程费用,其表达式如式(10)。

式中,QCU,i、QHU,j分别为冷、热公用工程换热量;CCU、QHU分别为冷、热公用工程费用系数;ACU,i、AHU,j、Ai,j,k分别为冷公用工程单元、热公用工程单元和换热器单元的换热面积;C1'、C2'、C3'分别为冷公用工程单元、热公用工程单元和换热器单元的面积费用系数;C1、C2、C3分别为冷公用工程单元、热公用工程单元和换热器单元的固定投资费用;B为面积费用指数。
考察优化后换热网络的总换热量与其对应的热流均匀性因子之间的关系,所得结果如图4所示。从图4中可以看出,换热网络的总换热量Q与热流均匀性因子φ'q,net两条曲线成相反趋势,能够形成换热量越大,热流均匀性因子越小的对应关系,且在同一横坐标处换热量有最大值时,热流均匀性因子具有最小值。虽然存在一定的误差但总体上能够形成较好地对应,由此可以说明本研究建立的换热网络热流均匀性因子能作为优化后换热网络换热效能的评价指标,从而能够利用该热流均匀性因子指导换热网络的综合及优化。
2.2 算例二
算例二采用文献[21-23]中的10股流换热器网络来检验及分析换热网络中的热流均匀性因子与换热性能之间的关系,该换热网络由6股热流体和4股冷流体组成,流股的初始参数见表2,文献[21]中优化的结构如图5所示。
在图5所示的结构基础上随机改变各换热器的冷、热流体匹配,规定每股流体上至多匹配4个换热器,同一位置至多匹配一个换热器,以此获得30个不同的换热网络结构,以换热网络年综合费用F为目标函数,换热器单元面积A为变量,采用牛顿法对每个结构进行优化,获得30个换热网络的优化结构。

图4 换热量与热流均匀性因子φ'q,net的关系图

表2 算例2的流体参数

图5 文献[21]优化的换热网络结构

图6 换热量与热流均匀性因子φ'q,net的关系图
考察优化后换热网络的总换热量与其对应的热流均匀性因子之间的关系,所得结果如图6所示。从图6中可以看出,换热网络的总换热量Q与热流均匀性因子φ'q,net之间总体上能够形成换热量越大,热流均匀性因子越小的对应关系。通过对该算例中热流均匀性因子的验证,说明本研究所建立的换热网络的热流均匀性因子能够作为优化后换热网络换热效能的一种新的评价指标,且该热流均匀性因子能为换热网络的综合及优化提供一种新的思路。
3 结论
本研究从能量有效利用的角度出发,在换热网络的温差均匀性因子及场协同理论的基础上,提出并建立了换热网络的热流均匀性因子,通过两个具体的实例对换热网络热流均匀性因子进行验证及分析,得到以下结论。
(1)根据各换热器的换热量进行加权计算得到的热流均匀性因子与总换热量之间能形成更好的对应关系,能够更准确地反映换热网络的换热效能。
(2)换热网络的热流均匀性因子比温差均匀性因子更适于评价换热网络的换热效能,使用的范围更加广泛。
(3)不同优化结构的换热网络热流均匀性因子与总换热量之间能够形成较好的对应关系。
总之,本研究所建立的换热网络的热流均匀性因子总体上能够反映换热网络的换热效能,该因子能够作为换热网络换热效能的一种评价指标,并能利用该因子指导换热网络的综合及优化。
[1] Linnhoff B,Hindmarsh E.The pinch design method for heat exchanger networks[J].Chemical Engineering Science,1983,38(5):745-763.
[2] 赵野,孙琳,罗雄麟.多程换热网络综合与夹点技术研究进展[J].化工进展,2012,31(8):1685-1689.
[3] Yee T F,Grossmann I E.Simultaneous optimization for heat integration-II.Heat exchanger network synthesis[J].Computers and Chemical Engineering,1990,14(10):1165-1183.
[4] 周聪海,黄智贤,邱挺,等.随机搜索算法在换热网络优化中的应用进展[J].化工进展,2012,31(3):495-501.
[5] Ravagnani M A S S,Silva A P,Arroyo P A,et al.Heat exchanger network synthesis and optimization using genetic algorithm[J].Applied Thermal Engineering,2005,25(7):1003-1017.
[6] Lin B,Miller D C.Solving heat exchanger network synthesis problems with Tabu search[J].ComputersandChemical Engineering,2004,28(8):1451-1464.
[7] 过增元,李志信,周森泉,等.换热器中的温差场均匀性原则[J].中国科学,1996,26(1):25-31.
[8] 过增元.热流体学[M].北京:清华大学出版社,1992.
[9] 吕岩岩,崔国民,郭佳,等.多股流换热器设计的量纲1温差均匀性优化因子[J].化工学报,2007,58(10):2476-2480.
[10] 崔国民,吕岩岩,张勤.换热器网络温差场分析及温差均匀性因子的建立[C]//中国工程热物理学会传热传质学术会议论文集,南京,2006:1608-1611.
[11] 吕岩岩.场协同下的换热器网络整体强化技术研究[D].上海:上海理工大学,2009.
[12] 崔国民,吕岩岩,胡向柏.换热网络整体强化技术及其温差均匀性因子[C]//中国工程热物理学会传热传质学术会议论文集,郑州,2008:454.
[13] H.哈肯.协同学:理论与应用[M].杨炳弈译.北京:中国科学技术出版社,1990.
[14] 过增元,黄素逸,等.场协同原理与强化传热新技术[M].北京:中国电力出版社,2004.
[15] 崔国民,卢洪波,李美玲.场协同条件下的换热器恒热流换热研究[C]//中国工程热物理学会传热传质学会议论文集,上海,2002:1029-1032.
[16] 过增元.对流换热的物理机制及其控制:速度场与热流场的协同[J]. 科学通报,2000,45(19):2118-2122.
[17] Bjork Kaj-Mikael,Nordman Roger.Solving large-scale retrofit heat exchanger network synthesis problems with mathematical optimization methods[J].Chemical Engineering and Processing,2005,44(8):869-876.
[18] 胡向柏,崔国民,涂惟民,等.换热网络填充函数法的全局优化[J].化学工程,2011,39(1):28-31.
[19] 张勤,崔国民,关欣.基于蒙特卡罗遗传算法的换热网络优化问题[J].石油机械,2007,35(5):19-22.
[20] 胡向柏,崔国民,许海珠,等.换热器优化顺序对换热网络全局优化的影响[J].化工进展,2012,31(5):987-1003.
[21] Khorasany R M,Fesanghary M.A novel approach for synthesis of cost-optimal heat exchanger networks[J].Comput.Chem.Eng.,2009,33(8):1363-1370.
[22] Yerramsetty K M,Murty C V S.Synthesis of cost-optimal heat exchanger networks using differential evolution[J].Comput.Chem.Eng.,2008,32(8):1861-1876.
[23] Ravagnani M A S S,Silva A P,Arroyo P A,et al.Heat exchanger network synthesis and optimization using genetic algorithm[J].Appl.Therm.Eng.,2005,25(7):1003-1017.
