微分进化算法优化换热网络的性能

方大俊，崔国民，万义群，许海珠

（上海理工大学新能源研究所，上海 200093）

换热网络是化工过程中一个重要的子系统，换热网络优化的节能效果也一直是该行业重要的研究热点。虽然各国学者已经过数十年深入研究，然而，换热网络的全局最优化仍然是过程系统优化的疑难问题。一是由于换热网络本身模型是属于一种混合整数非线性问题（MINLP）[1]，具有严重的非凸、非线性等特性，导致在整个可行解领域内局部最优解星罗棋布。二是优化理论与优化方法还不完善。现有的针对换热网络问题的优化方法主要分为数学规划法[2-4]与启发式方法[5-6]。数学规划法在用于换热网络优化时，随着换热网络规模的增大，局部最优解的组合呈现着指数形式的增长，数学规划法很容易陷入质量不好的局部最优解当中。其次，数学规划法优化换热网络时，跟初始点的关系十分密切。即使同一个网络结构，在初始点不同时，不但优化得到的局部最优解不同[7]，而且很难得到该结构下的最优解。

启发式方法是一种全局优化方法，能够跳出局部最优解，具有很强的全局搜索能力，近年来，来越多的研究者研究与应用。微分进化算法[8-9]是启发式算法的一种，是Storn和Price在1995年首次提出应用。微分进化算法搜索引擎极其简单，但十分有效。尤其是针对连续性变量，已被证明是一种有效的全局优化方法。

本文作者首先针对一给定结构，通过改变换热器面积证明了换热网络在在着严重的非线性特性及局部最优解众多的特点；其次通过实例，给定不同的初始点下，分别用牛顿法和微分进化算法进行优化，结果证明传统的牛顿法在不同的初始点下优化得到不同的局部最优解，而本研究所采用的微分进化算法在优化换热网络问题时，不但不受初始点的影响，而且优化精度得到进一步的提高，该算法在求解换热网络问题时收敛稳定，具有很好的鲁棒性及全局搜索能力。

1 换热网络模型

假设有Nc股冷流体需要加热，Nh股热流体需要冷却而达到各自的目标温度。换热网络为达到节能并且减少费用投资的情况下，在冷、热物流之间加换热器的能量回收网络。已知物流参数包括物流入口温度、热容流率入各换热器的换热系数。同时，有一组固定的冷公用工程与一组热公用工程，用来冷却与加热未达到目标温度的流体，公用工程的换热系数与进出口温度已知。以二股热流体，三股冷流体Grossmann分级超结构[10]为例，其结构表达方式如图1所示，级数Sk=max(Nc，Nh)。

换热网络优化以综合费用为目标函数，包括年操作费用与投资费用。操作费用主要与公用工程消耗量有关，而投资费用主要与换热面积及换热设备台数有关。在不考虑固定投资的情况下，目标函数的数学形式如式（1）。

式中，z代表换热器存在与否的逻辑变量；C1、C2分别为换热器面积费用系数与公用工程的费用系数；A表示换热器面积；Q为公用工程的换热量；N为流体数目；Sk为级数；b为面积费用指数；c、h代表冷、热流体；u代表公用工程；k代表第k级；i、j分别代表位于第i与第j股流体。例如式(zC2Q)cu2中，z、C2、Q分别表示位于第2股热流体上换热器逻辑变量、冷公用工程费用系数、冷公用工程换热量。

2 换热网络的非线性特性分析

换热网络优化属于 MINLP问题，其严重的非线性不仅与对数平均温差、换热系数及非线性函数有关，而且跟目标函数中的换热器面积的非线性形式有很大的关系。即使在固定的结构下，由于可行域内换热器面积的众多组合变化，将会导致换热网络在最优化过程中存在着大量的局部最优解，给数学规划法优化换热网络带来巨大障碍。本节针对具体的算例，在固定换热网络结构的条件下，分析换热器面积与综合费用之间的非线性关系。

算例取自文献[11-14]，由6股热流体与4股冷流体组成，参数与文献相同。所有流体的流股参数与计算公式如表1所示。换热器面积费用计算式为60×A$/(m2·a)，热公用工程费用为 100×Qh$/(kW·a)，冷公用工程费用为 15×Qc$/(kW·a)，所有换热器换热系数为0.025 kW/(m2·℃)。

为研究换热器面积与综合费用之间的非线性关系，给换热网络任意匹配12个换热器并保持结构不变，给定所有换热器面积为200 m2，如图2所示。在固定该结构与给定面积的条件下，变动 1号、4号换热器的面积，得到面积变化与综合费用变化如图3所示。

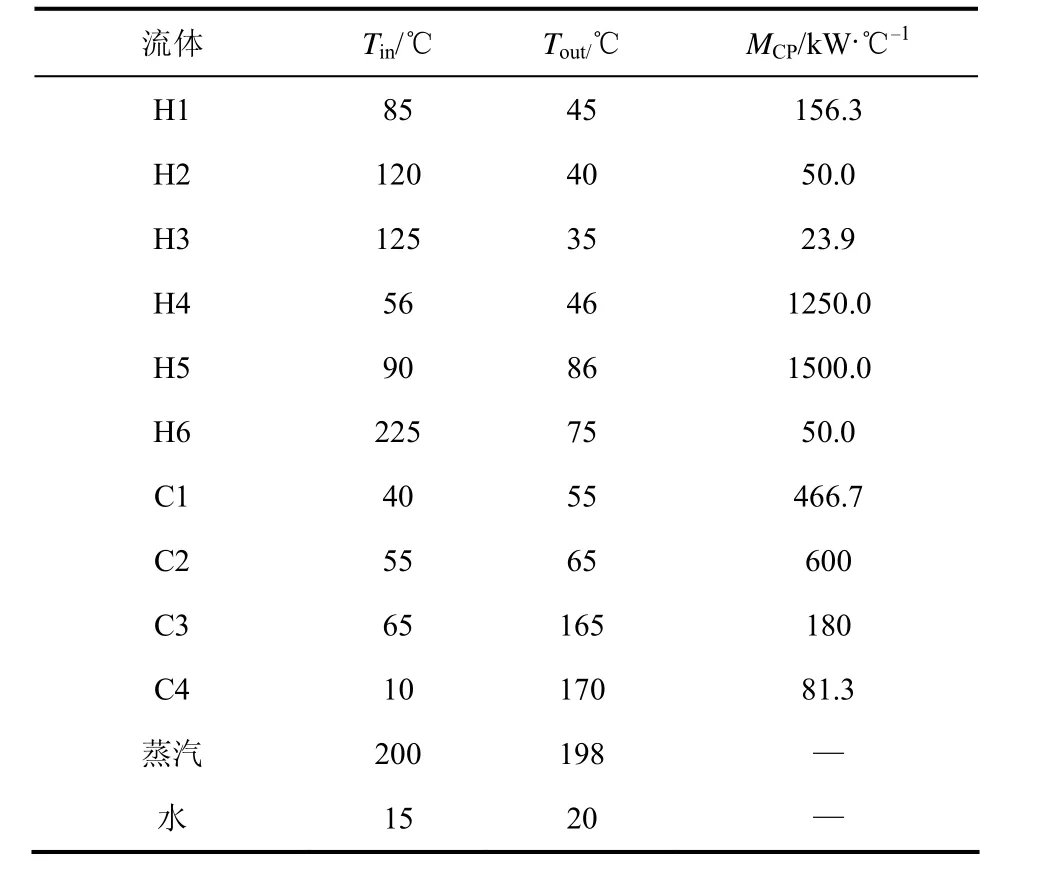
表1 流体参数

由图3可以看出，仅仅变动两个换热器面积，在限定范围内，就存在一个极值点，可见换热器面积的变化使得换热网络优化问题存在着大量的局部最优解，这将给全局寻优过程带来很大障碍。

3 微分进化算法

微分进化算法是一种基于群体进化的算法，具有记忆个体最优解和种群内信息共享的特点，即通过种群内个体间的合作与竞争来实现对优化问题的求解，是一种有效的无约束全局最优化方法。优化过程主要分为3个部分。设定一定规模的种群数量后，不断地经过变异、交叉、选择的进化过程向最优解逼近。而换热网络优化问题为有约束问题，设利用惩罚函数法转化后的无约束问题为M(X)，应用微分进化算法求解换热网络优化问题步骤如下所述。

（1）初始化参数。种群规模N，交叉概率P，缩放因子C，最大迭代步数g（初始为0）。随机产生N组换热网络初始解，每一组解中包含n个需要优化的换热器面积。种群表示为：X={X1，g，··，Xi，g··，Xn，g}。其中，Xi,g={xi,g(1),xi,g(2),··xi,g(j)··，xi,g(n)}，Xi，g为第g代第i个个体；xi,g(j)为第g代种群中第i个个体的第j个换热器面积。其中P、C∈[0，1]。

（2）变异。对种群中每个个体的每个换热器面积采用变异机制如式（2）。

式中，vi,g(j)为第g代种群中第i组的第j个换热器变异面积，其中，n1、n2、n3为随机产生互不相同的整数。

因为换热器面积不能为负，因此，增加边界限制条件，对变异后的换热器面积处理如式（3）。

（3）交叉。对种群中所有个体的变量逐个产生均匀分布随机数cr∈[0，1]，采用二项交叉。执行方式如式（4）。

式中，xi,g'(j)：第g次迭代第i组中第j个换热器的试验面积；rnd为随机产生位于[1，n]的整数。

（4）选择。当该初始点的所有换热器面积执行完变异与交叉过程，生成试验个体。比较该试验个体年综合费用与该个体上一轮的年综合费用，按贪婪选择的方式，选择较好的个体进代下一代搜索。如式（5）。

（5）终止条件。g达到最大进化代数时，终止优化。

相对于其它算法而言，微分进化算法是一种高效的并行算法，基于种群的全局搜索策略，具有独特的记忆能力，能够动态跟踪当前个体的搜索情况来调整逼近全局最优解的方向，不依赖于目标函数的梯度信息。因此，不易陷入换热网络局部最优解，具有较强的全局收敛能力与鲁棒的性能，因此能有效应用于换热网络优化[15]。

4 微分进化算法优化换热网络问题的稳定性

由于换热网络问题严重的非线性特征，即使在固定换热网络结构的条件下，也具有大量的局部最优解。而传统的局部优化方法常常依赖于目标函数的梯度信息，不仅容易陷入局部最优解；并且难以摆脱初始点的影响，在不同的初始点下，会陷入不同的局部最优解。本节通过实例，在不同的初始点下，分别运用牛顿法与微分进化算法优化换热网络问题，比较结果证明，牛顿法容易受初始点的影响，陷入不同的局部最优解，而微分进化算法具有很好的鲁棒性，不受所给初始点的影响，解的稳定性较强。

以牛顿法为例，在不同的初始点下，优化上节的换热网络固定结构。给定全部换热器的初始面积分别为A1=200 m2与A2=1000 m2进行优化，牛顿法优化得到的局部最优年综合费用分别为$ 5645133和$ 5644129，优化后各换热器面积见表2与表3。在相同结构的条件下，利用微分进化算法进行优化，分别设定随机产生初始个体面积在200 m2与1000 m2附近，所产生不同的初始面积优化后均能得到年综合费用为$ 5631282，所得面积如表4所示。有力地证明了该算法不仅鲁棒性强、求解稳定、不受初始点的影响，而且能在一定的程度上提高优化精度，降低换热网络的年综合费用，节约生产成本。

表2 初始点为200 m2优化结果换热器面积

表3 初始点为1000 m2优化结果换热器面积

表4 微分进化算法优化所得换热器面积

5 结 论

本研究首先通过改变换热器面积，分析了求解换热网络的障碍在于换热网络优化问题严重的非线性特性、局部最优解众多的特点，同时，传统的局部优化方法优化时容易受初始点的影响，优化时陷入不同的局部最优解，收敛稳定性很差。因此，基于换热网络分级超结构模型，在给定不同初始面积的条件下，分别采用牛顿法及微分进化算法对换热网络实例进行优化，优化结果表明，牛顿法在不同的初始面积下得到不同的优化结果，而微分进化算法求解换热网络优化问题时，优化结果不受初始点的影响，稳定性强，鲁棒性好，而且能进一步提高优化精度，降低年综合费用，节约生产成本。

[1]Furman，K C，Sahinidis N V.Computational complexity of heat exchanger network synthesis[J].Computer Chemical Engineering，2001，25：1371-1390.

[2]Linnhoff B，Hindmarsh E.The pinch design method for heat exchanger networks[J].Chemical Engineering Science，1983，38（5）：745-763.

[3]Kesler M G，Parker R.O.Optimal networks of heat exchange[J].Chemical Engineering Process Symposium Series，1969，65：111 -120.

[4]Ignacio E Grossmann，Jose Antonio Caballero，Hector Yeomans.Mathematical programming approaches to the synthesis of chemical process systems[J].Korean Chemical Engineering，1999，16（4）：407-426.

[5]Lewin D R，Wang H，Shalev O.A generalized method for HEN synthesis using stochastic optimization—Ⅰ.General framework and MER optimal synthesis[J].Computers and Chemical Engineering，1998，22（10）：1503-1513.

[6]Lewin D R.A generalized method for HEN synthesis using stochastic optimization—ⅡThe synthesis of cost-optimal networks[J].Computers and Chemical Engineering，1998，20（10）：1387-1405.

[7]胡山鹰，陈丙珍，何小荣.连续性变量全局优化的模型退火法[J].系统工程理论与实践，1995，9（9）：73-80.

[8]Price K，Storn R，Lampinen J A.Differential evolution：A practical approach to global optimization[M].Berlin Heidelberg：Springer-Verlag，2005.

[9]Rainer Stron，Kenneth Price.Differential evolution——A simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization，1997，11：341–359.

[10]Yee T F，Grossmann I E，Kravanja Z.Simultaneous optimization models for heat integration I.Area and energy targeting and modeling of multi-stream exchangers[J].ComputersandChemical Engineering，1990，14（10）：1151-1164.

[11]Ahmad S.Heat exchanger networks：Cost trade-offs in energy and capital[D].PhD thesis，UMIST，Manchester，UK，1985.

[12]Ravagnani M A，Silva A P，Arroyo P A Constantino.Heat exchanger network synthesis and optimisation using genetic algorithm[J].Applied Thermal Engineering， 2005， 25（7）：1003–1017.

[13]Yerramsetty K M，Murty C V S.Synthesis of cost-optimal heat exchanger networks using differential evolution[J].Computers and Chemical Engineering，2008，32（8）：1861-1876.

[14]Mohammadhasani Khorasany R，Fesanghary M.A novel approach for synthesis of cost-optimal heat exchanger networks[J].Computers and Chemical Engineering，2009，33（8）：1363-1370.

[15]方大俊，崔国民.微分进化算法应用于换热网络全局最优化[J].化工学报，2013，64（9）：3285-3290.