基于分数阶微积分的岩土材料变形研究

段晓梦，殷德顺，李彦青，张 伟

(河海大学力学与材料学院，江苏南京 210098)

岩土材料的变形特性十分复杂，剪缩剪胀性是其最大特点之一。现有的剪缩剪胀研究多以常规三轴压缩试验为基础，针对不同种类的岩土材料提出了相应的本构关系或变形理论［1－2］。然而这些研究得到的理论模型多以某一种特定岩土材料的试验结果为基础，适用性有所局限。模型参数大多形式复杂，实际应用不够便捷。另外，现有的岩土材料变形研究更多地关注体积变形，很少有人探讨横向－纵向应变关系的问题。笔者认为材料的横向－纵向应变关系的复杂性是导致变形特性复杂的主要原因。

材料的横向－纵向应变关系常用泊松比来表示。Tschoegl等［3］将黏弹性材料具有时间依赖性的泊松比记为ν(t)，从而在某些情况下可以用ε'=－ν(t)ε描述黏弹性材料的横向-纵向应变关系。但对于不同的加载方式，ν(t)具有不同的表达式，且形式较为复杂，应用时不够简洁。另外，泊松比的本质是横向-纵向应变关系，泊松比研究的根本目的是为了能够便捷地通过纵向应变求出横向应变。而黏弹性材料泊松比较理想弹性材料的泊松比复杂得多，所以笔者希望通过直接探讨横向-纵向应变关系来研究岩土材料的变形特性。

分数阶微积分作为数学理论的一个重要分支，已被成功用于许多复杂现象的研究中，诸如黏弹性力学［4］、电磁学［5］、动力学［6］等领域。殷德顺等［7］还将分数阶微积分应用于岩土材料流变模型的研究中。利用分数阶微积分建立的物理模型能够较好地描述具有记忆及时间依赖性的物理现象，且具有参数少、形式简单的优点。因此，笔者尝试用分数阶微积分建立一种既能较好地描述岩土材料剪缩剪胀现象，又形式简单、参数少，还能适用于多种岩土材料的变形模型。分数阶微积分的定义有很多种，笔者基于Riemann－Liouville定义的分数阶微积分［8］建立岩土材料分数阶横向-纵向应变关系和分数阶体积应变模型，希望探索一条研究岩土材料变形的新思路。

1 分数阶岩土应变模型

1.1 分数阶横向-纵向应变关系

对于理想弹性材料，应力与应变之间遵循虎克定律，即σ=Eε。对于非理想弹性材料，Smit等［9］基于分数阶微积分，提出了分数阶应力应变本构模型:

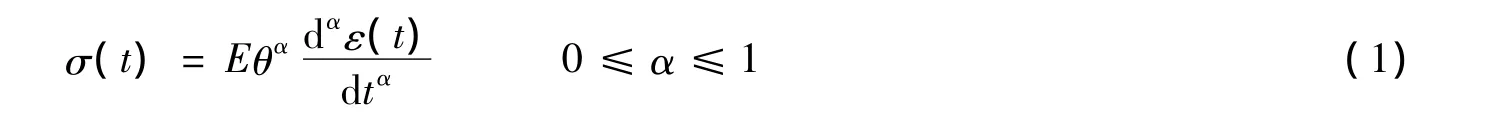
式中:E，θ——材料常数;α——分数阶阶数。

模型(1)利用了分数阶微积分的优点，具有参数少、形式简单的特点，能够反映材料力学性质的时间依赖性。

在弹性力学中，对应于虎克定律有横向-纵向应变关系式ε'=－νε，其中ε'表示横向应变，ε表示纵向应变。在Wong等［10］的研究中，可以发现软骨在应力松弛时荷载随时间的变化曲线与体积随时间的变化曲线很相似。因此，可以设想是否也存在着一种与分数阶应力应变关系相对应的分数阶横向-纵向应变关系，于是笔者大胆地提出如下公式(即分数阶横向-纵向应变关系):

式中:φ，η——材料常数;β——应变关系分数阶阶数，能够反映黏弹性材料在不同条件下的变形特性及变形能力，与材料性质及加载条件等有关。

当β=0时，式(2)能够退化成ε'=－νε，此时式(2)中的φ就成为材料的泊松比ν。如果β是常量，则φηβ也是常量，可记为λ。在等应变率加载时，纵向应变表示为ε=ν0t(ν0为常数)。通过式(2)可以得到

式(3)就是等应变率加载时的分数阶横向-纵向应变关系。根据式(3)可以得到β取不同值时的|ε'|～|ε|理论曲线(图1)。由于式(2)中对时间求导，致使λ的量纲与泊松比ν的不相同，所以λ并不是材料的泊松比，类似于式(1)中的参数Eθα描绘了具有流变性的非理想弹性材料的性质，与材料的微观结构特性有关，其明确的物理意义有待进一步研究。

1.2 分数阶体积应变

在一定条件下，体积应变可以表示为 εv=ε+2ε'。将式(3)代入该式能够得到等应变率加载时的分数阶体积应变公式:

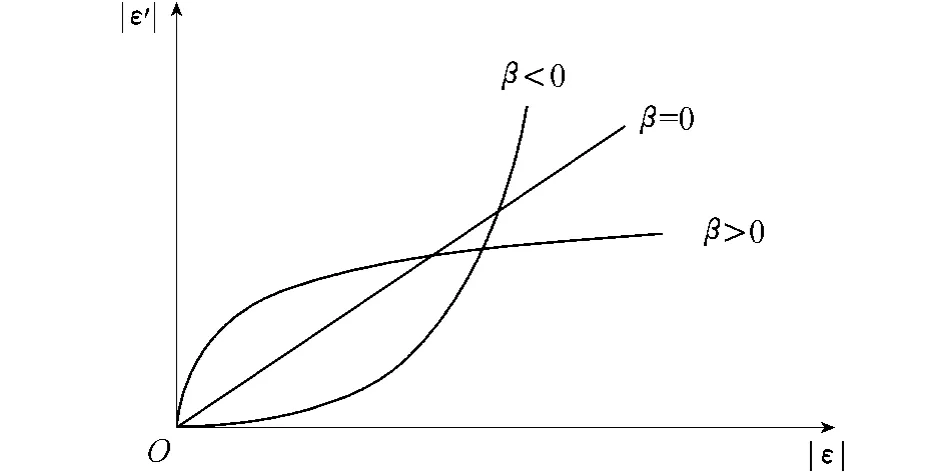
图1 等应变率加载|ε'|～|ε|理论曲线Fig.1 |ε'|-|ε|theoretical curves at a constant longitudinal strain rate

根据式(4)，当－1＜β＜0且ε＜0，即材料受压时，β取不同值可得如图2所示的理论曲线。这些曲线分别描述岩土材料在常规三轴压缩试验中的剪缩与剪胀现象。容易发现，分数阶微积分在变形建模中能够发挥其巨大优势:新模型参数少、形式简单，能够充分反映材料变形的时间依赖性，且参数易于确定，适用性广泛，并能合理描绘岩土材料的剪缩剪胀性。

2 模型验证

由于岩土不能受拉，而高分子材料是典型的黏弹性材料，所以首先利用高分子材料来验证拉伸加载时分数阶变形模型的正确性，然后再通过3种具有代表性的岩土材料的变形数据来验证分数阶变形模型在常规三轴压缩情况下的正确性。根据式(3)可知横向应变与纵向应变之间呈幂函数关系，所以，只要提供相应的对数关系便能获得相关参数。笔者建立的模型在应力松弛和等应变率加载情况下能够推导出解析应变关系公式，不需要数值算法。如果遇到复杂的加载情况，可以通过数值算法求解。有关分数阶微积分的数值算法问题可以参阅文献［8］。

2.1 高分子材料等应变率拉伸变形

Addiego等［11］曾研究过高密度聚乙烯在等应变率单轴拉伸时的体积变形。通过式(3)和式(4)，可以得到|ε'|～|ε|和εv～ε的拟合曲线(图3)。他们在研究中发现高分子材料在等应变率拉伸初期，试件的体积几乎保持不变，甚至会发生微量收缩。通过图3可以知道，分数阶变形模型不仅能够很好地模拟高分子材料的变形行为，还能够描述试件在加载初期体积发生微量收缩的现象。

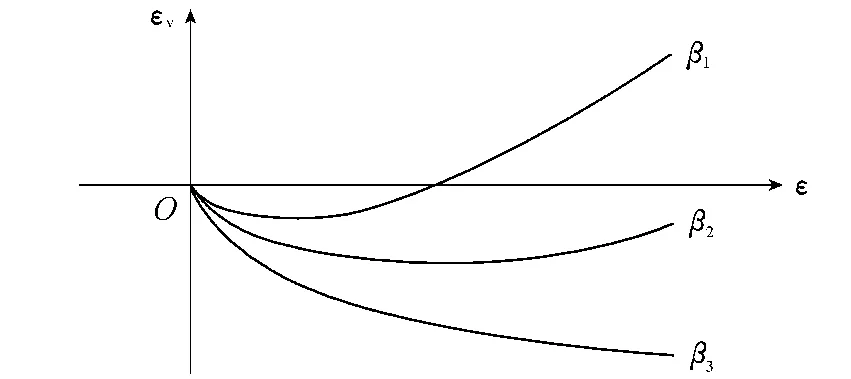
图2 等应变率加载时的εv～ε曲线示意图Fig.2 εv-ε theoretical curves at a constant longitudinal strain rate

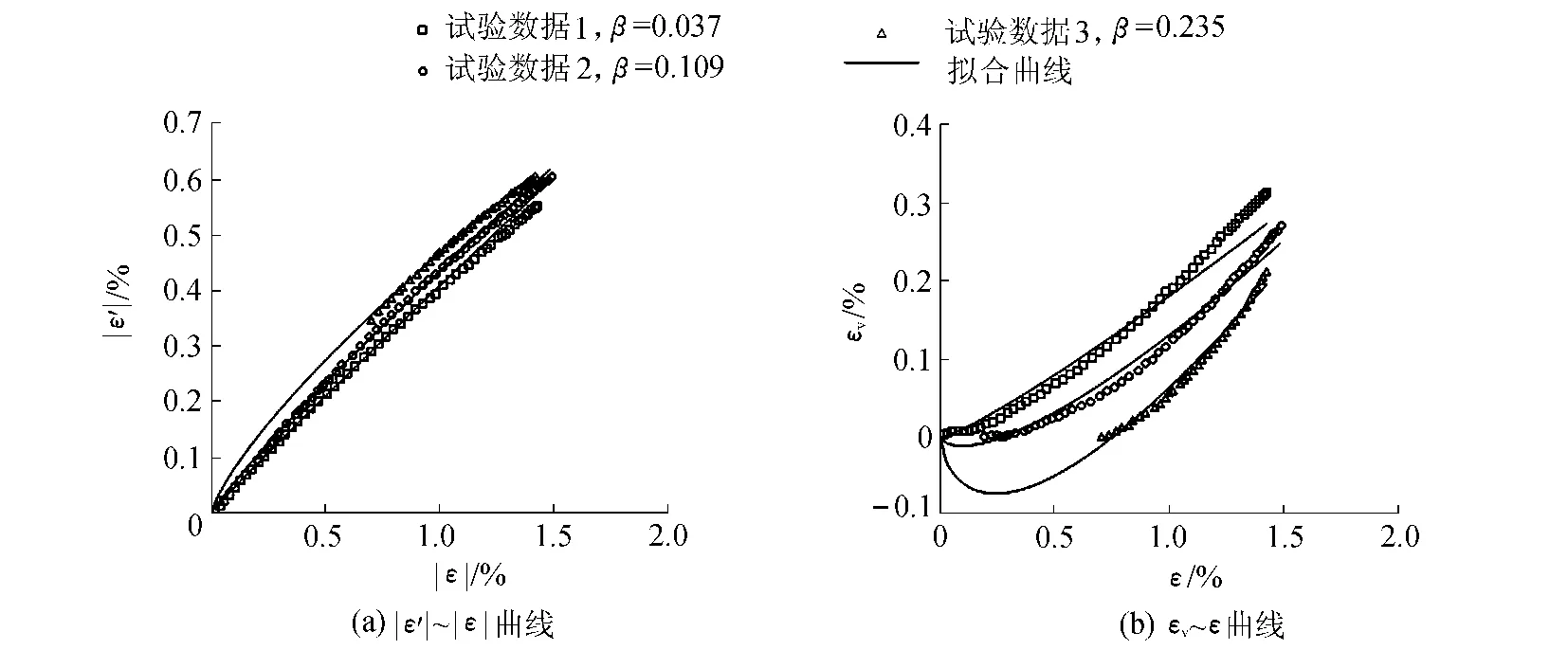
图3 高密度聚乙烯等应变率拉伸应变曲线Fig.3 Strain curves at a constant longitudinal strain rate for high-density polyethylene

2.2 岩土材料常规三轴压缩变形

常规三轴压缩试验是测量可变形固体力学性质的一种有效方法，其加载过程可分为2个阶段:第1阶段，将恒定应力加到试样上，直至试样应变不再变化;第2阶段，在第1阶段加载基础上施加一个逐渐增大的应力σ1－σ3，或一个变化的纵向应变ε1。对于第2阶段，如果纵向应变ε1只与σ1－σ3有关，则可以等同于单轴压缩试验。因此，针对单轴加载的分数阶变形模型可用于常规三轴试验。

李治［12］和刘萌成等［13］分别对黏土和堆石料做过常规三轴压缩试验研究，得到一系列试验数据。利用式(3)和式(4)，可以得到|ε'|～|ε|和εv～ε的拟合曲线，分别如图4和图5所示。由图4、图5可知，笔者建立的分数阶横向-纵向应变关系与岩土材料的实际变形情况较吻合。

研究发现:等应变率拉伸时β为正，压缩时β为负。众所周知，材料拉伸和压缩时其内部力学行为是有区别的，而β的正负号变化正好能够表征这种差别。随着围压σ3的增加，β值不断减小(绝对值增大)，表明β能反映常规三轴压缩试验中围压对岩土材料剪缩剪胀性的影响。从多孔介质角度考察岩土材料，其变形行为是孔隙水和土颗粒运动的外在反映，即β可以反映孔隙水和土颗粒的运动行为。综上所述，β实际上是岩土材料在不同加载条件下其内部复杂运动机理的宏观度量。当然，β如何与材料内部行为相对应还需要结合相关研究进行深入探讨。另外，笔者发现即使有些|ε'|～|ε|曲线相当接近直线(β值接近零)，但却不能用直线来拟合，否则在拟合体积应变时将出现误差。

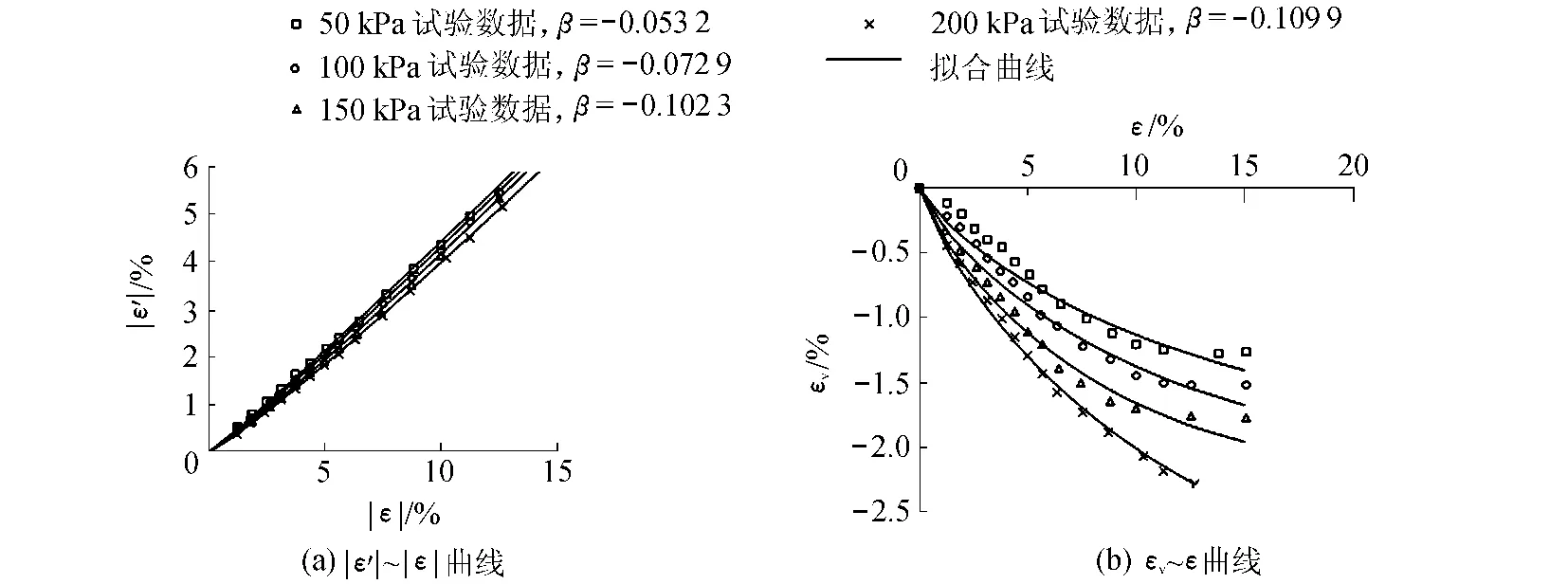
图4 黏土常规三轴压缩试验应变曲线Fig.4 Strain curves for clay in triaxial compression tests

3 结 论

a.分数阶变形模型具有分数阶模型的参数少、形式简单的优点。

b.分数阶横向－纵向应变关系符合岩土材料的实际变形情况，能够较好地拟合试验数据。

c.岩土材料的剪缩剪胀现象能够被分数阶体积应变模型合理地描述。β能反映常规三轴压缩试验中围压对于岩土材料剪缩剪胀性的影响。

d.虽然一些岩土材料的横向－纵向应变关系近似线性关系，但若用线性关系来描述，会在描述其体积变形时产生误差。

e.模型如何扩展为三维，以及将该理论模型与计算机数值算法相结合，是需要继续关注的方向。

［1］赵星光，蔡明，蔡美峰.岩石剪胀角模型与验证［J］.岩石力学与工程学报，2010，29(5):970－981.(ZHAO Xingguang，CAI Ming，CAI Meifeng.A rock dilation angle modle and its verification［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29(5):970－981.(in Chinese))

［2］迟明杰.砂土的剪胀性及本构模型的研究［D］.北京:北京交通大学，2008.

［3］TSCHOEGL N W，KNAUSSW G，EMRI I.Poisson's ratio in linear viscoelasticity:a critical review［J］.Mechanics of Time－Dependent Materials，2002，6(1):3－51.

［4］LEWANDOWSKI R，CHORAŽYCZEWSKI B.Identification of the parameters of the Kelvin－Voigt and the Maxwell fractional models，used to modeling of viscoelastic dampers［J］.Computers ＆ Structures，2010，88(1/2):1－17.

［5］JESUS I S，MACHADO J A T.Implementation of fractional－order electromagnetic potential through a genetic algorithm ［J］.Communications in Nonlinear Science and Numerical Simulation，2009，14(5):1838－1843.

［6］SAHA R S，CHAUDHURI K S，BERA R K.Analytical approximate solution of nonlinear dynamic system containing fractionalderivative by modified decomposition method ［J］.Applied Mathematics and Computation，2006，182(1):544－552.

［7］殷德顺，任俊娟，和成亮，等.一种新的岩土流变模型元件［J］.岩石力学与工程学报，2007，26(9):1899－1903.(YIN Deshun，REN Junjuan，HE Chengliang，et al.A new rheological model element for geomaterials［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26(9):1899－1903.(in Chinese))

［8］陈文，孙洪广，李西成.力学与工程问题的分数阶导数建模［M］.北京:科学出版社，2010.

［9］SMIT W，de VRIESH.Rheological models containing fractional derivatives［J］.Rheologica Acta，1970，9(4):525－534.

［10］WONG M，PONTICIELLO M，KOVANEN V，et al.Volumetric changes of articular cartilage during stress relaxation in unconfined compression ［J］.Journal of biomechanics，2000，33(9):1049－1054.

［11］ADDIEGO F，DAHOUN A，G'SELL C，et al.Characterization of volume strain at large deformation under uniaxial tension in high－density polyethylene［J］.Polymer，2006，47(12):4387－4399.

［12］李治.模拟基坑应力路径的真三轴平面应变试验研究［D］.南京:河海大学，2006.

［13］刘萌成，高玉峰，刘汉龙.堆石料剪胀特性大型三轴试验研究［J］.岩土工程学报，2008，30(2):205－211.(LIU Mengcheng，GAO Yufeng，LIU Hanlong.Study on shear dilatancy behaviors of rockfills in large－scale triaxial tests［J］.Chinese Journal of Geotechnical Engineering，2008，30(2):205－211.(in Chinese))