基于新型本构模型的胶凝堆石坝多目标优化

明 宇，蔡 新，，郭兴文，武颖利，杨 杰

(1.河海大学水文水资源与水利工程科学国家重点实验室，江苏南京 210098;2.河海大学水利水电学院，江苏南京 210098;3.河海大学力学与材料学院，江苏 南京 210098;4.南京水利科学研究院岩土工程研究所，江苏南京 210024)

胶凝堆石坝作为一种兼有混凝面板堆石坝和混凝土重力坝优点的新坝型，因其断面小、施工速度快、用料节省、便于施工导流、抗震性能好、适应较软弱地基，因此具有很强的竞争力和推广应用前景。但由于目前对该坝型筑坝材料特性的研究不足，使得对其工作性态认识不清，常把它看作普通堆石坝或者若干不同坝坡组合的体型优选［1-2］进行设计，其经济性、安全性等方面的优点不能被客观地体现，阻碍了该坝型的推广应用。笔者依据文献［3］提出的新型本构模型，在研究胶凝堆石坝工作性态的基础上，综合考虑安全性和经济性要求，对其进行优化设计研究，为该坝型的设计提供科学依据，从而推动该坝型的发展和广泛应用。

1 胶凝堆石料本构模型

胶凝堆石料是采用少量水泥、粉煤灰、砂砾石等拌和而形成的固结体，是一种“超贫混凝土”，其材料特性介于普通堆石料和混凝土之间，本构关系具有明显的非线性。文献［3］在胶凝堆石料的抗压强度试验、抗折强度试验和大三轴试验的基础上，通过对试验数据的回归分析和参数反演，分别从压缩状态、拉伸状态等方面考虑，提出了胶凝堆石料的弹性非线性本构模型，并采用该模型对自身试验以及孙明权等［4］的胶凝堆石料三轴试验进行了数值模拟，模拟结果与试验结果非常接近，验证了该模型的合理性［3］。各应力状态下胶凝堆石料本构关系如下:

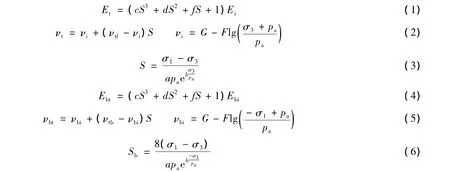
式中:Et，Ei，νt，νi，S——压缩状态下的切线弹性模量、初始弹性模量、切线泊松比、初始泊松比和应力水平;Ebt，Ebi，νbt，νbi，Sb——拉伸状态下的切线弹性模量、初始弹性模量、切线泊松比、初始泊松比和应力水平;σ1，σ3——第一、第三主应力;pa——标准大气压力;νtf，νtb——压缩阶段和拉伸阶段破坏时的泊松比，本文均取0.49;a，b，c，d，f，G，F——材料的试验参数。e 近似取 2.71828。

2 胶凝堆石坝体型多目标优化设计

借助大型通用有限元分析软件ANSYS的APDL参数化语言和优化求解器，将胶凝堆石料的本构模型模块开发到ANSYS程序中［5－7］，对胶凝堆石坝进行非线性有限元分析，并通过参数化建模输出模型的应力、位移和稳定等约束条件，调用ANSYS中的优化模块对所建立的数学模型进行可行域内的寻优搜索［8－9］，实现对该坝型断面的优化设计。ANSYS的优化模块提供了2种优化方法，即函数逼进法和梯度寻优法，前者不容易陷入局部极值点，但优化精度较低，适合大范围普适的粗优化，而后者是一种局部寻优的精优化方法［10］。因此笔者先采用函数逼进法初步求得最优解的基本位置，然后再采用梯度寻优法对最优解的位置进行更精确的确定。

2.1 胶凝堆石坝结构计算模型

以成屏面板堆石坝为优化设计原型，对其典型断面进行有限元数值模拟，建立胶凝堆石坝有限元模型如图1所示。筑坝材料采用胶凝体积质量为60 kg/m3，密度为2250 kg/m3的胶凝堆石料，坝高74.6 m，坝顶宽5 m，上、下游坝坡均为1∶1.3，正常蓄水位为71.6 m。采用接触单元来模拟混凝土面板和堆石体之间的接触面，坝底设置竖向和水平向约束，大坝分20 级施工。本构方程(1)～ (6)中 a，b，c，d，f，G，F分别取 28.13，0.112，－0.7415，0.4762，－0.7343，0.223，0.001。

2.2 胶凝堆石坝优化设计数学模型

进行胶凝堆石坝体型优化需要同时考虑坝体的经济性和安全性。坝体的断面面积直接反映了坝体的经济性，而坝体在蓄水期的最大水平位移、最大沉降和最大应力水平可以反映坝体的整体刚度和强度储备。由于胶凝堆石坝的坝坡稳定性很强［11］，在优化设计时可不予考虑。坝坡变陡可以使该坝型的经济性得到充分体现，但却降低了坝体的整体刚度和强度储备［11］。本文采用多目标优化思想，基于面板堆石坝与混凝土重力坝的有关设计规范［12－13］，将设计变量选为上、下游坝坡坡度x1，x2，对胶凝堆石坝的经济性、最大位移和最大应力水平等多个目标进行综合分析。

根据胶凝堆石坝的结构特点和工作性态，库水压力作用于上游坝坡，优化设计时的约束条件一般取以下形式:

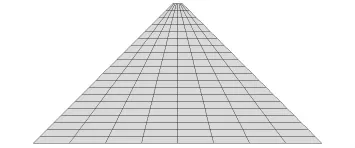
图1 胶凝堆石坝有限元模型Fig.1 Finite element model of CSG dam

a.几何约束。根据国内外工程经验，建造在基岩上的面板堆石坝上、下游可采用1∶1.3～1∶1.5的坝坡，碾压混凝土坝的下游坝坡一般为1∶0.6～1∶0.8。考虑到胶凝堆石坝的坝坡一般介于普通面板堆石坝与碾压混凝土坝之间，可取胶凝堆石坝的x1，x2的上、下限为1∶1.5～1∶0.6，且剔除上游缓、下游陡的情况。

b.性态约束。在强度方面，由于目前缺少胶凝堆石坝的设计规范，笔者依据试验结果和有限元分析结果对大坝进行强度约束。由三轴试验可知，当胶凝堆石料的最大应力水平S*达到0.8时材料开始发生剪切破坏，因此要求载荷产生的坝体S*不能超过0.8;由胶凝堆石料的抗压试验、抗折试验和强度安全系数研究［11］可知，胶凝体积质量为60 kg/m3的胶凝堆石料的允许抗压强度［fcu］和抗拉强度［fct］分别为2.68 MPa和0.34 MPa，已知混凝土面板的允许抗拉强度［σ］=1.0 MPa，所以本文要求坝体最大主应力σ1≤0.34 MPa，最小主应力绝对值|σ3|≤2.68 MPa，面板最大顺坡向应力σmax≤1.0 MPa。在稳定性方面，为保证胶凝堆石坝的整体稳定性，根据混凝土重力坝设计规范，应使大坝的整体抗滑稳定安全系数K≥［K］=1.10［13］，计算公式如下:

式中:f——坝体和地基间的摩擦系数，取f=tanφ=0.863;φ——胶凝堆石料的内摩擦角下限，取40.8°;P1——坝体自重;P2——作用在上游坝坡的水压力;P3——水荷载对坝体产生的水平推力。

为使目标函数兼顾经济性与安全性，首先将坝体的断面面积进行无量纲处理。令上、下游坝坡为1∶1.5的坝体断面面积为A*，优化断面面积为Aa，定义坝体的经济系数φa=Aa/A*，则φa的值越小，断面的经济性越高;以最大水平位移和最大沉降量为标准反映坝体的整体刚度，令φw=0.5(Xa/X*+Ya/Y*)，X*和Y*分别为最大水平位移与最大沉降量允许值(取坝坡为1∶0.6时的计算值)，Xa和Ya分别为优化断面情况下的最大水平位移和最大沉降量，φw越小坝体的整体刚度越大;从三轴试验结果可知，当S*=0.8时，胶凝堆石料开始发生塑性剪切破坏，因此S*反映了坝体的强度储备。令系数φs=Sa/S*，其中Sa为优化断面的最大应力水平，φs越小则坝体的强度储备越高。

目标φa与目标φw，φs具有相互排斥性，采用线性加权的统一目标法将多目标问题化为单目标优化问题，权重系数 ωi描述各个目标的影响程度［14］，ωi满足 ∑ωi=1，因此目标函数 F(X)=ω1φa+ω2φw+ω3φs。

综上所述，图1所示的基本结构的最优化设计数学模型如下:求设计变量

使目标函数

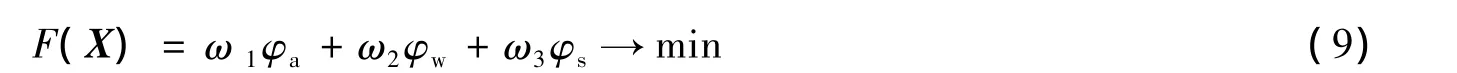
满足约束条件

2.3 优化设计结果及分析

根据上述优化设计数学模型，考虑对称断面(x1=x2)与不对称断面(x1≥x2)2种情况，经济系数权重ω1取0.1，0.2，0.3，…，0.8，0.9来进行胶凝堆石坝断面优化设计(φw，φs等权重)。计算结果表明，当 ω1=0.1时，优化方案的断面面积大于原坝型，不能体现该坝型的经济性，因此这里只列出ω1=0.2，0.3，…，0.7，0.8，0.9的16种优化方案结果，见表1、表2。

表1 对称断面优化结果及最大应力、位移Table 1 Optimization results of symmetrical sections and maximum values of stress and displacement

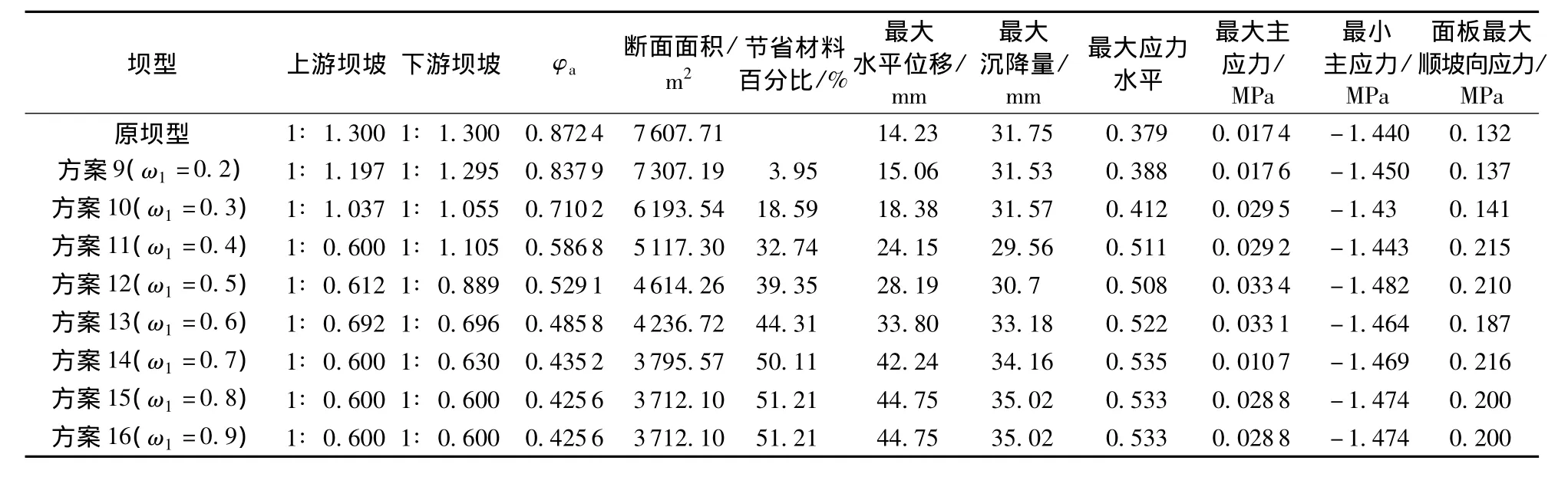
表2 不对称断面优化结果及最大应力、位移Table 2 Optimization results of non-symmetrical sections and maximum values of stress and displacement

由优化结果可以看到，较之原坝体断面，各优化方案的断面面积有不同程度的减小。随着ω1的提高，优化断面面积呈减小趋势，该坝型的经济性越明显(当ω1=0.8时，优化结果的上、下游坝坡均达到约束临界值1∶0.6)，同时坝体的最大位移和最大应力水平均有不同程度的增大，但都在允许范围之内，而最大、最小主应力的变化不明显。通过比较表1和表2可以发现，在ω1相同的情况下，对称断面的优化面积较小，从而φa较小，如图2所示。

从图2可以看出，当ω1相同时，2种断面形状的优化目标函数F(X)大致相同，只是φa存在较大差异，这里可理解为对称断面坝型牺牲了一定的断面面积来提高断面的经济性，却降低了坝体的整体刚度和强度储备，这也符合文献［11］中总结的规律。总体来说，经过优化调整，各优化方案在满足安全约束的前提下，都不同程度地减小了坝体断面面积，节省了工程成本，达到了优化设计的目的。

图2 各方案φa与F(X)Fig.2 Economic coefficients and target functions of all schemes

3 结 论

a.通过胶凝堆石坝的体型优化设计研究，得到兼顾经济性与安全性的系列最优设计方案，各方案的非劣解都是可行解，满足规定的约束条件，其差别在于强度储备和工程量的多少，可以根据专家经验、实际工程需要或应力控制标准等因素选定最优解。

b.通过对比对称断面与不对称断面的优化设计方案可知，在两者各权重系数相同的情况下，对称断面更能体现该坝型的经济性，而不对称断面则有较大的整体刚度和强度储备，因而有更好的安全性。

c.与原坝型设计方案相比，优化设计方案具有明显的优越性，各优化设计方案均在满足安全约束的同时降低了工程成本，因此本文建立的优化设计数学模型合理有效，可为胶凝堆石坝的设计提供参考。

［1］蔡新，施金，郭兴文，等.胶凝面板堆石坝优化设计［J］.水利水电科技进展，2008，28(1):43-45.(CAI Xin，SHI Jin，GUO Xingwen，et al.Optimal design of cemented concrete face rockfill dam［J］.Advances in Science and Technology of Water Resources，2008，28(1):43-45.(in Chinese))

［2］CAI Xin，WU Yingli，YI Jiangang，et al.Research on shape optimization of CSG dams［J］.Water Science and Engineering，2011，4(4):443-454.

［3］蔡新，武颖利，李洪煊，等.胶凝堆石料本构特性研究［J］.岩土工程学报，2010，32(9):1340-1344.(CAI Xin，WU Yingli，LI Hongxuan，et al.Constitutive equation for CSG materials［J］.Chinese Journal of Geotechnical Engineering，2010，32(9):1340-1344.(in Chinese))

［4］孙明权，彭成山，李永乐，等.超贫胶结材料三轴试验［J］.水利水电科技进展，2007，27(4):46-49.(SUN Mingquan，PENG Chengshan，LI Yongle，et al.Triaxial test of over lean cemented material［J］.Advances in Science and Technology of Water Resources，2007，27(4):46-49.(in Chinese))

［5］师访.ANSYS二次开发及应用实例详解［M］.北京:中国水利水电出版社，2012.

［6］宿辉，党承华，崔佳佳.邓肯-张非线性模型研究及其在ANSYS中的实现［J］.中国农村水利水电，2010(3):76-79.(SU Hui，DANG Chenghua，CUI Jiajia.Duncan-Chang nonlinear elastic model and realization in ANSYS［J］.China Rural Water and Hydropower，2010(3):76-79.(in Chinese))

［7］吴业飞，马海霞.基于ANSYS的土石坝应力变形有限元分析［J］.水利与建筑工程学报，2010，8(4):209-212.(WU Yefei，MA Haixia.Finite element analysis on stress deformation of earth-rock dam based on ANSYS［J］.Journal of Water Resources and Architectural Engineering，2010，8(4):209-212.(in Chinese))

［8］穆全平，辛全才.基于ANSYS的软基重力坝剖面优化设计［J］.人民长江，2009，40(24):19-23.(MU Quanping，XIN Quancai.Optimization design of gravity dam on pebble foundation based on ANSYS［J］.Yangtze River，2009，40(24):19-23.(in Chinese))

［9］SAEED M.Finite element analysis:theory and application with ANSYS［M］.New York:Prentice Hall，2007.

［10］商跃进.有限元原理与ANSYS应用指南［M］.北京:清华大学出版社，2005.

［11］武颖利.胶凝堆石坝坝料力学特性及大坝工作性态研究［D］.南京:河海大学，2010.

［12］SL 319—2005 混凝土重力坝设计规范［S］.

［13］SL 274—2001 碾压式土石坝设计规范［S］.

［14］孙文俊，孙林松，王德信，等.拱坝体形的两目标优化设计［J］.河海大学学报:自然科学版，2000，28(3):39-43.(SUN Wenjun，SUN Linsong，WANG Dexin，et al.Bin objective shape optimization of arch dams［J］.Journal of Hohai University:Natural Sciences，2000，28(3):39-43.(in Chinese))