直线度误差统计模型识别的实验方法
2013-10-11黄丽玲黄富贵
黄丽玲,黄富贵
(华侨大学 机电及自动化学院,福建 厦门361021)
直线度是几何量测量中形位误差的最基本参数之一,也是评价机械产品质量的一项重要指标.国家标准GB/T 1958-2004《产品几何量技术规范(GPS)形状和位置公差 检测规定》规定:形位误差是指被测提取要素对其拟合要素的变动量.形位误差测量的提取、滤波、拟合与评定是新一代GPS有关几何量测量标准的重要环节,合理规范这些环节的要求无疑对形位误差测量的具体操作有重要的指导意义[1].提取是形位误差测量的首要环节,其主要内容是提取方案和提取点数的确定.提取方案与提取点数的确定合理与否将影响到形位误差的测量评定结果.尽管相关标准中已经对提取作了相应的规定,但是这些规定都较为笼统,难以指导具体的测量工作[2-4].形位误差测量的提取是通过对被测形位误差对象几何要素线的连续信号进行离散采样,并要求采样后的离散信号能不失真地反映被测对象形位误差信息的操作.目前,研究提取点数最广泛使用的方法为计算机仿真[5-6],而仿真技术的关键在于能够事先得到形位误差的统计特征规律,进而才能以此为模型进行仿真.因此,掌握被测形位误差对象的连续信号的规律,特别是信号的统计特征规律是提取点数确定准则建立的前提.由于导致实际机械零件形位误差的因素包括机床、刀具、加工方法、操作人员的技术水平、环境等多种因素,因此不少学者认为形位误差对象信号近似服从正态分布统计规律,有关的学者也从理论上证明了部分形位误差项目服从正态分布的规律[7].但是,这一结论并未经实践检验.本文详细介绍在视频仪上对零件平面内直线度误差的几何要素线的大提取点数的提取方法,并以提取得到的几何要素线上的坐标数据为样本,采用统计直方图与正态性D检验法结合的方法识别出给定平面内直线几何要素线的误差统计模型.
1 直线度误差的测量实验
实验采用的检测原则为测量坐标值原则,提取方案为布点提取方案,以JVP300型视频仪为测量设备进行直线轮廓边缘的坐标数据获取,在测量环境温度为(25±1)℃的实验室条件下,对平面内的直线度误差的几何要素线进行测量.表1为实验对象的信息.表1中:l为零件直线长度;f为直线度误差;IT为公差等级;a,b,c,d为4组测量的点数 .
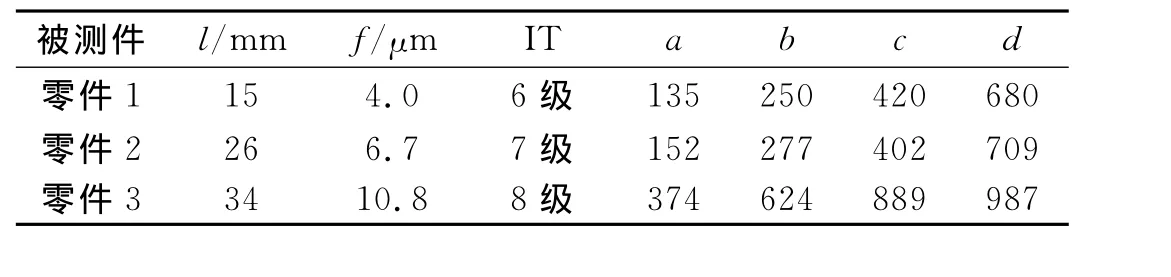
表1 测量实验对象信息Tab.1 Information of the measured experimental objects
对3个零件的被测表面直线度误差的几何要素线分别作4组不同点数(a,b,c,d)的测量,得到所测点的坐标;然后,将各组坐标数据(xi,yi),i=1,2,…,n导入 MATLAB软件中进行初步分析,可得到实测坐标点(xi,yi)到最小二乘拟合直线的距离h的统计直方图,如图1所示.
从图1的统计直方图的分布情况大致可以判断出,每个零件的4组数据都呈现出正态分布的趋势,但为严格验证其正态性,需进一步做以下检验.
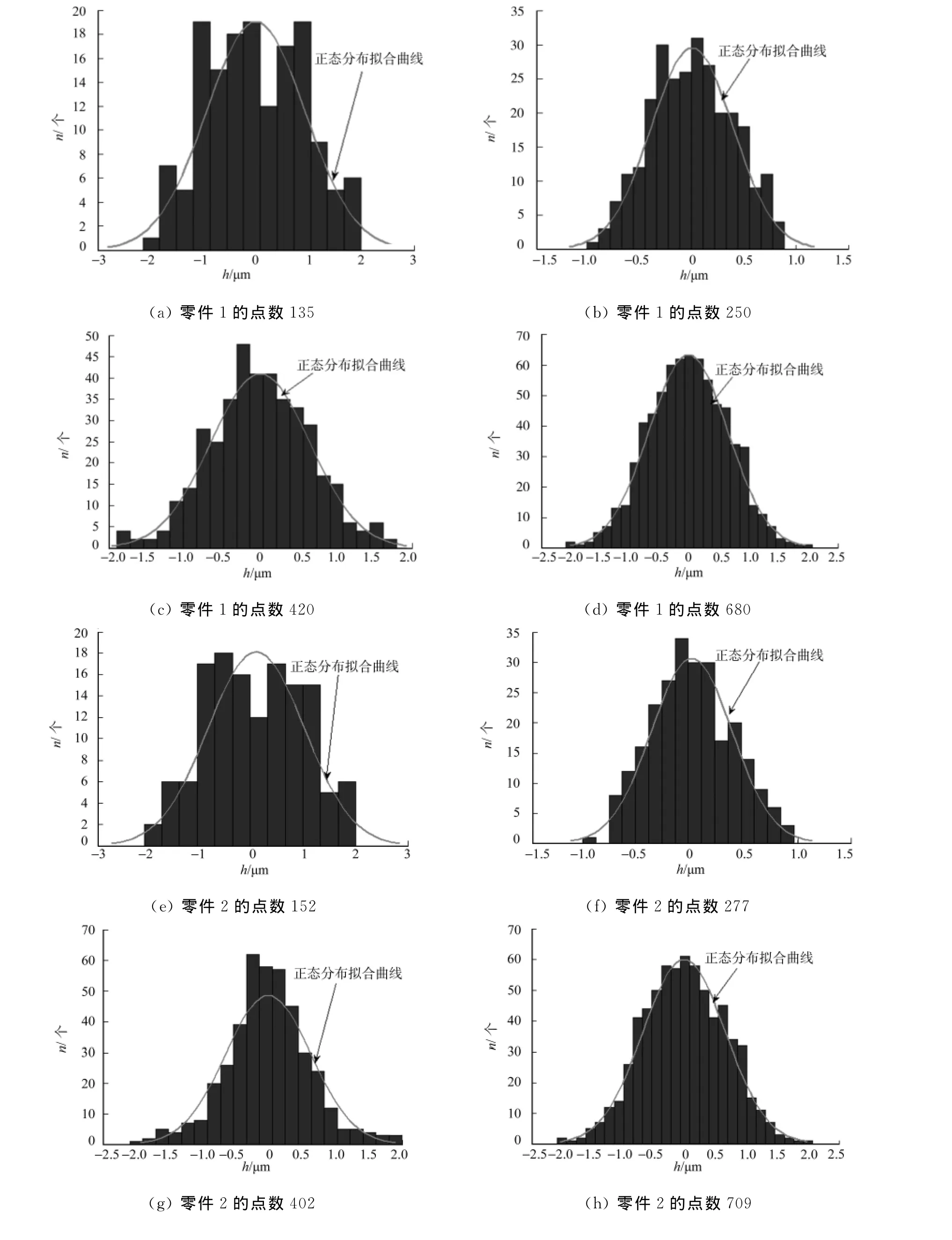
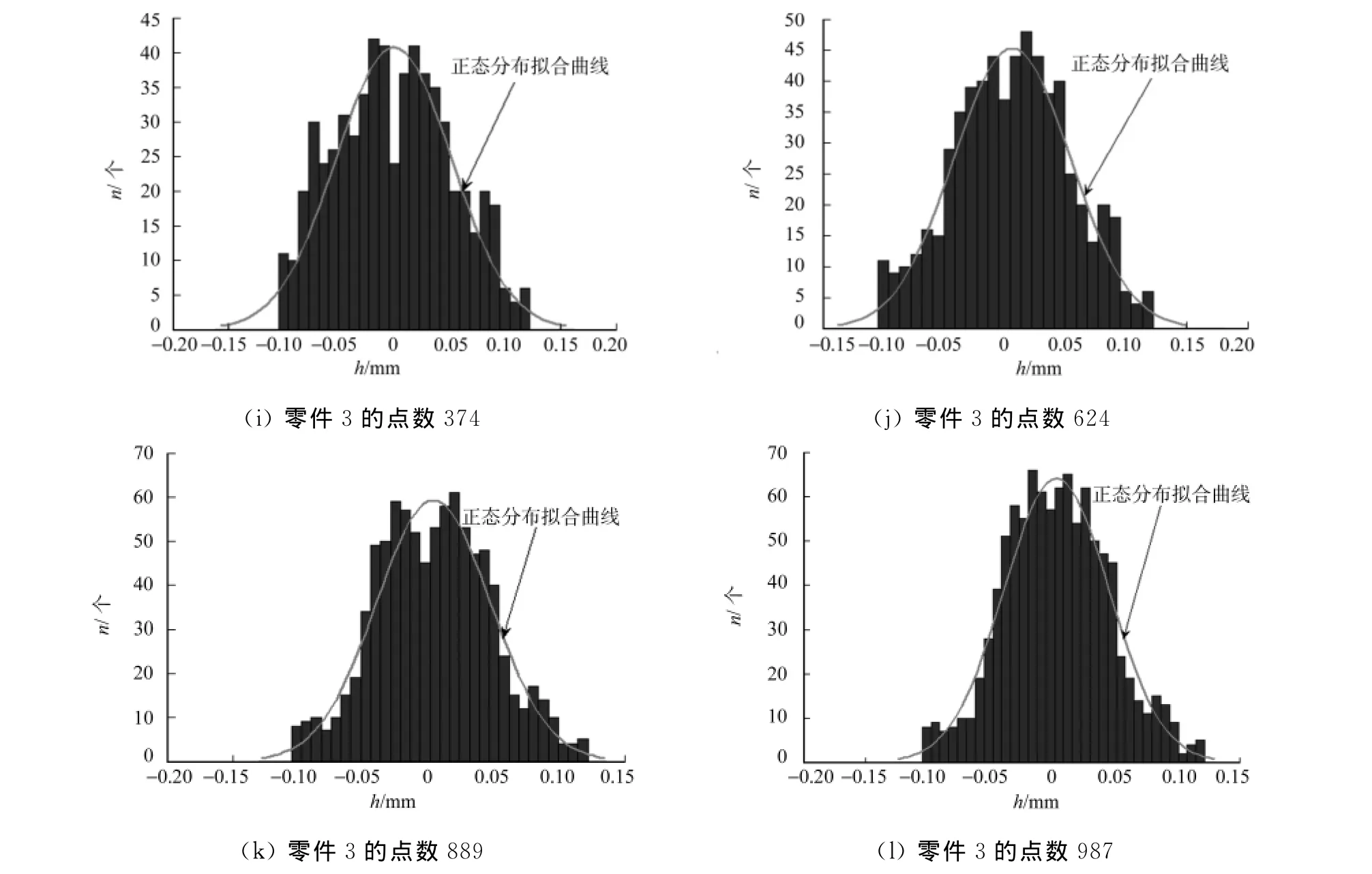
图1 点到最小二乘拟合直线距离的统计直方图Fig.1 Histogram of the distance between point and least square fitting lines
2 测量数据的正态性检验
根据国家标准GB/T 4881-2001《数据的统计处理和解释 正态性检验》的规定,当样本的容量为50~1 000时,需要使用正态性D检验法检验样本是否符合正态分布[8-9].具体的D检验法有如下3个主要的步骤.
1)将由数据(xi,yi),i=1,2,…,n处理得出坐标点到最小二乘拟合直线的距离h按照非降次序排列成X(1)≤X(2)≤…≤X(n).
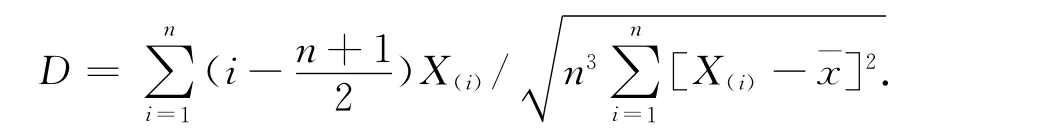
3)选定显著性水平α=0.05,由D检验法临界表查得Zα/2和Z1-α/2.若Zα/2≤Y≤Z1-α/2,则原样本服从正态分布;否则,不服从正态分布.
零件的4组数据的验算结果,如表2所示.表2中:无法查到的值是采用线性插值法计算得到的.
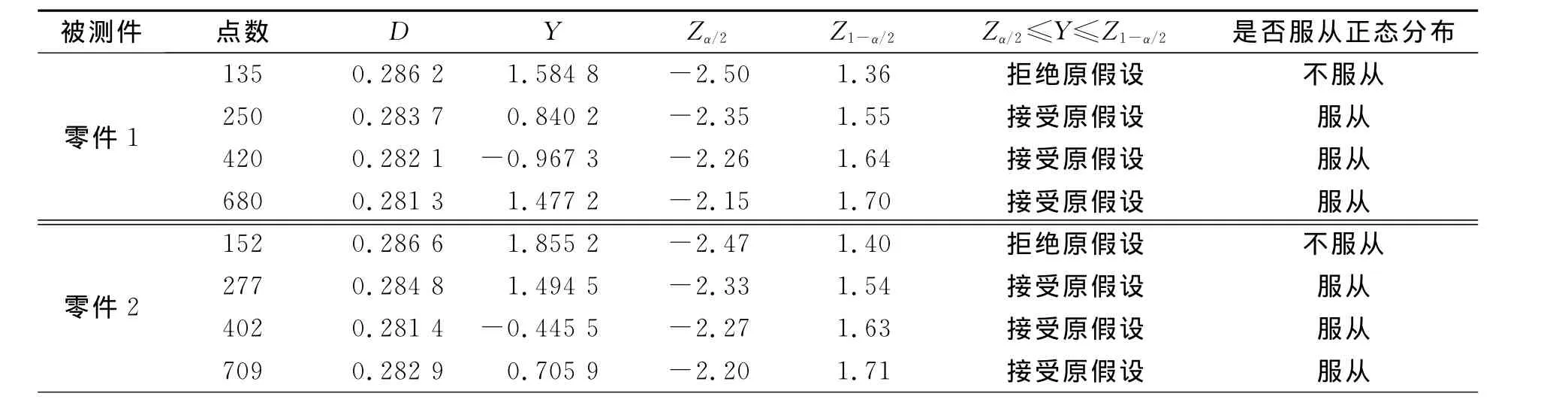
表2 测量数据的正态性检验Tab.2 Normality tests of the measured experimental data

续表Continue table
由表2可知:当点数较少时,直线度误差测量统计模型不服从正态分布的规律,可由其统计直方图可得出其近似服从正态分布的规律,正是由于其测量点数较少,导致其正态性不显著 .所以,当点数逐渐增多时正态性愈加显著;而当测量点数增加到一定量时,都能服从正态分布的规律.
3 结束语
构建在视频测量仪器上实现对某零件表面直线度误差测量坐标点的采集,采用统计学理论的正态性D检验法对实验数据进行检验,得到零件表面直线度误差统计模型服从正态分布规律的结论 .此结论为直线度误差测量提取点数的计算机仿真研究奠定基础,同时为其他形位误差项目测量提取点数确定准则的建立提供参考.
[1] 张琳娜,王铭,郑玉花.新一代GPS中提取与滤波、拟合操作间关联特性的研究[J].机械强度,2010,32(2):293-298.
[2] 张琳娜,郑玉花,郑鹏.基于 GPS的提取操作模型及其应用规范研究[J].机械强度,2007,29(4):632-636.
[3] 郑玉花,张琳娜,庆科维.新一代GPS的提取方案及其应用研究[J].机械设计与制造,2008(6):193-194.
[4] 黄富贵.直线度误差评定的测量提取点数选择[J].华侨大学学报:自然科学版,2011,32(6):615-617.
[5] 黄富贵,郑育军.直线度误差测量采样方案的研究[J].工具技术,2007,41(10):95-98.
[6] 程真英,陈晓怀,薄晓静,等.蒙特卡罗在圆度测量精度分析中的应用研究[J].仪器仪表学报,2006,27(6):1262-1263.
[7] 倪骁骅,邓善熙.形状误差的分布类型及评定模型[J].兰州理工大学学报,2007,33(6):36-39.
[8] 梁小筠.正态性检验(一)[J].上海统计,2000(10):45-50.
[9] 俞钟行.D检验法[J].地质与勘探,1990,26(2):45-46.
