基于EMD的无参考图像清晰度评价方法

贺金平 阮宁娟 何红艳

（北京空间机电研究所，北京100094）

1 引言

目前数字图像质量（Quality）的评价可以分为主观评价和客观评价。主观评价测试不仅繁琐、耗时而且实行起来相当昂贵，而且还会受到观测者专业背景、心理和动机等主观因素的影响[1]，并且不能结合到其它算法中使用。这使得在很多情况下都不方便进行主观测试。客观图像质量评价方法分为全参考型（Full Reference，FR）、部分参考型（Reduced Reference，RR）和无参考型（No Reference，NR）3种。由于NR算法无需参考图像，灵活性强，近年来，NR图像质量评价受到越来越多的学者关注。

不同的评价方法对于压缩、模糊、加性噪声等不同失真类型和图像内容（自然场景、人物、指纹、编织袋等）的敏感度不同。本文算法主要针对的是模糊这种失真类型进行图像清晰度评价，主要应用于优化或评价复原算法、图像获取与处理一体化优化设计的像质评价等方面[2-4]。

清晰度指图像上各纹理及边界的清晰程度，是衡量图像质量的重要指标之一。传统的无参考图像信噪比（SNR）估算只是对信号和噪声的数学统计，由于具体统计方式的局限性，用于评价清晰度会与主观评价产生不一致现象。目前已有的清晰度评价方法主要有频谱函数、图像熵函数和灰度变换函数等多种函数[5-7]。频谱函数需进行傅里叶变换（或小波变换），计算量大，运算效率低；图像熵是基于统计模型的全局评价参数，也会产生与主观评价不一致的情况；灰度变换函数是基于清晰图像比模糊图像的灰度变化剧烈这一先验知识，通过统计灰度变化频率构造清晰度评价函数。目前灰度变换函数主要有梯度函数、点锐度函数等[8]，但都是在空域统计某一方向的灰度变化情况。然而，绝大部分复原算法对不同频率内容的复原效能不均匀，若在某一方向上某频率占主导，则会导致这类函数没有评价全频段复原特性，这样得到的评价结果会与主观评价结果存在较大偏差，所以应该对不同频率处的复原效能进行综合评定。

本文提出了一种基于经验模式分解（Empirical Mode Decomposition，EMD）的清晰度评价方法。图像经过EMD后，可以得到本征模式函数（Intrinsic Mode Function，IMF）图像和剩余图像。不同级的本征模式函数图像对应着不同的频率范围，通过统计多级本征模式函数图像极值的个数对复原效能进行综合评价，可以更全面的表征清晰程度。仿真模糊图像和遥感图像的试验结果证明，本文算法具有无参考、运算复杂度低、主客观评价一致性等特点。

2 经验模式分解方法

美国工程院院士N.E.Huang及其合作者于1998年首次提出了新的时频分析方法—Hilbert-Huang变换（HHT）。EMD方法的引入是该方法的创新。二维EMD是一种自适应多灰度尺度分解方法，其变换的基函数随图像的内容变化而变化，在图像处理方面具有天然的应用潜力，已被应用在图像压缩、图像去噪、图像融合、纹理分割、图像特征提取、图像放大等很多领域。

二维EMD原理如下[9]：

假设图像为I，av(I)表示对图像I求均值曲面，并且用avk( I)表示第k次对图像I求均值曲面，则原始图像与av(I)的差值就被定义为第一个IMF分量 c1，即

进而将原始图像与1c的差，即将第一次均值曲面av()I作为待处理图像再进行分解，就可得到第二个IMF分量；依次类推，可得出第n个IMF分量的分解表达式：

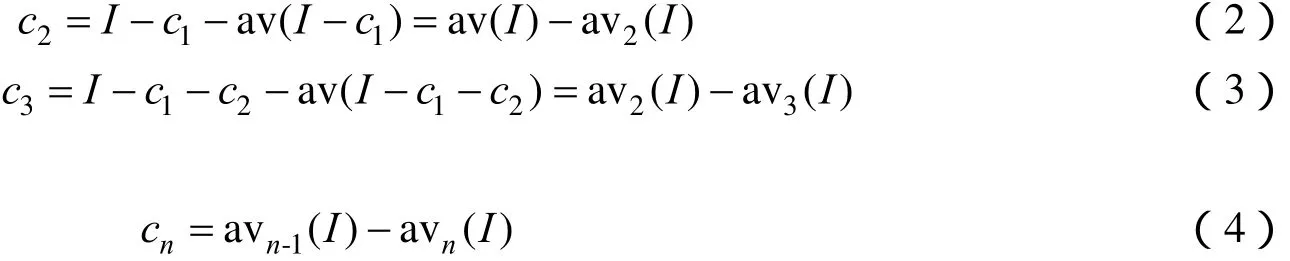
将式（1）～（4）相加，最终得到

由式（5）看出图像可以分解为多层IMF分量和剩余分量。第一个IMF分量包含了原始信号中最短的周期分量，每层IMF分量都代表了具有一定频率范围的模态；剩余分量为第k次均值曲面，是趋势项。

从基函数理论的角度来看，二维 EMD对不同内容的图像分解出的基函数ic是不同的。ic随图像内容变化而变化，它不同于傅里叶分解的基函数和小波分解的基函数（是预先确定的），其优势在于能够灵活有效地表示二维图像中具有多方向性的边缘和纹理等几何特性。

现有的二维EMD算法很大程度上依赖于二维插值方法[10]，拟合的包络曲面要足够平滑，并且经过每个数据点，还要避免边界上的过冲现象，以防止引入新的局部极值点。其分解方法具体步骤如下：

1）分别求出图像的上、下极值点包络曲面。首先，找出图像的局部极大值和极小值点，边界处应延展一定宽度；然后进行插值，分别求出极大值构成的极大值曲面和极小值构成的极小值曲面。

2）求均值曲面。均值曲面是极大值曲面和极小值曲面的平均值，该平均值曲面是该图像随空间变化的均值图像或轮廓。

3）提取图像的细节。用原图像减去该均值图像，就可得到图像的细节，即 IMF分量。均值图像可进一步按照步骤1）和2）分解出新一层IMF分量，依次类推，直到极大值、极小值包络曲面的中值小于某一阈值为止。

3 基于EMD的图像清晰度评价算法

本文算法主要通过统计各层IMF图像的灰度变化频率对图像清晰度作出评价。不同清晰度图像对应的相同层次的IMF分量图具有不同的灰度变化频率。由图1(b)和图2(b)对比可以看出：原图EMD后得到的第一层IMF分量的像素空间变化频率远远大于模糊后的第一层IMF分量。由图1(c)和图2(c)对比可得出相同的结论。

图1 Cameraman图像经验模式分解IMF分量图Fig.1 IMF images of the original Cameraman image after EMD

图2 散焦模糊图像经验模式分解IMF分量图Fig.2 IMF images of the defocusing blur image after EMD

利用这一特性，本文根据以下步骤构造了EMD图像清晰度参数：

1)输入待处理图像；

2)求图像的局部极大值点集、局部极小值点集，具体方法是在3×3邻域内选择最大值像素和最小值像素点；

3)分别对局部最大值点和局部最小值点进行插值，求得最大值点包络曲面和最小值点包络曲面；

4)计算最大值点包络曲面和最小值点包络曲面的代数均值，并将其作为均值曲面；

5)用输入图像数据减去均值；

6)判断是否满足每层的迭代停止条件。若满足则进入下一步；否则，用步骤5）中的结果，返回步骤3)进一步计算；

7)将结果作为分解得到的第i层IMF分量图；

8)判断是否满足图像分解结束条件。若满足进行步骤10）；否则转入步骤9）；

9)从待处理图像中减去此层信息，然后返回步骤1），进而计算第 1i+层IMF分量图；

10)得到n层IMF分量图和余量图；

11)统计EMD分解各个IMF分量图中的局部最大值个数和局部最小值个数；

12)按照式（6）计算EMD图像清晰度参数

本文构造的EMD图像清晰度参数统计了EMD中各个IMF分量图的像素空间变化频率，可以作为衡量图像纹理和边缘信息量的客观评价参数，且本算法无需原图或者原图的统计参数作为参考，是一种无参考的客观评价参数。

4 试验结果与分析

图像质量评价算法的目标是得到与人的主观评价相一致的评价结果，因此一致性是衡量算法性能的最主要方面。

本文的试验方法是在M atlab自带的4幅原始图像 Cameraman（256×256）、Lena（256×256）、Barbara（256×256）和 Peppers（512×512）上分别加不同程度的模糊，已知图像的清晰度与模糊的参数大小成反比，验证仿真图像的EMD清晰度参数与模糊参数也成反比。

图3为EMD清晰度参数随着位移像素数增加的拟合曲线，试验分别仿真了Lena和Cameraman在0°和 30°方向上运动 1、3、5、7、9个像素后的模糊图像。实际中，图像的模糊程度会随着位移像素个数的增加而加重，可以通过这一客观事实对EMD清晰度参数的一致性进行判断。由图3可以看出，随着位移像素个数的增大和运动角度的增大，EMD图像清晰度参数随之单调减小，与实际的图像清晰程度保持了很好的一致性。

图4为EMD清晰度参数随着散焦半径像素个数增加的拟合曲线，试验仿真了Barbara和Cameraman在散焦半径像素个数分别为3、4、5、6、7时的模糊图像。图5为EMD清晰度参数随着高斯模糊方差增加的拟合曲线，试验分别对Lena、Barbara、Peppers和Cameraman这4幅图像添加了模板为3×3，方差为0.1、0.2、0.3、0.4、0.5、0.6、0.7的高斯模糊。由图4和图5可以看出，EMD图像清晰度参数与实际的图像清晰程度保持了很好的一致性。

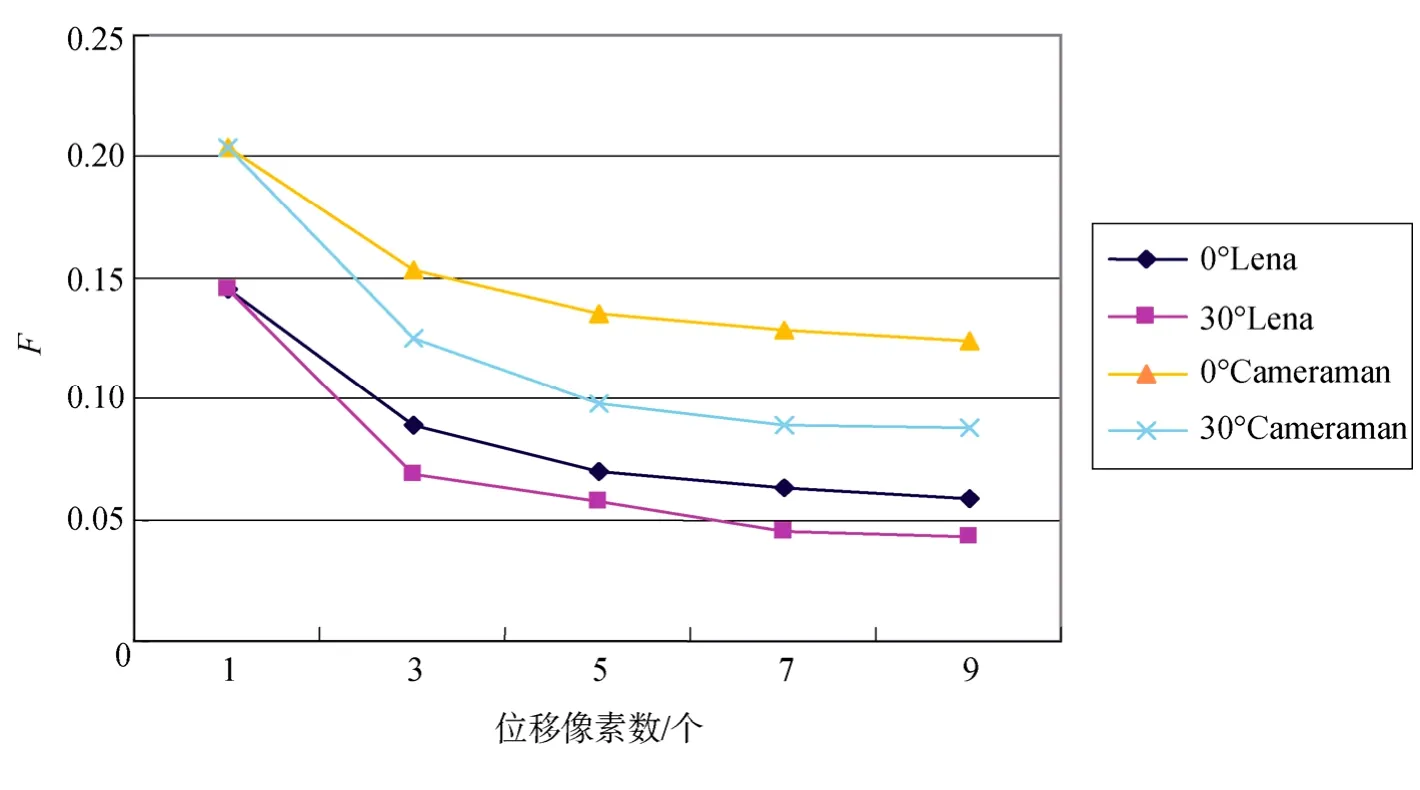
图3 运动模糊图像的EMD清晰度拟合曲线Fig.3 The fitted curve of EMD definition of motion blur images

图4 散焦模糊图像的EMD清晰度拟合曲线Fig.4 The fitted curve of EMD definition of defocusing blur images

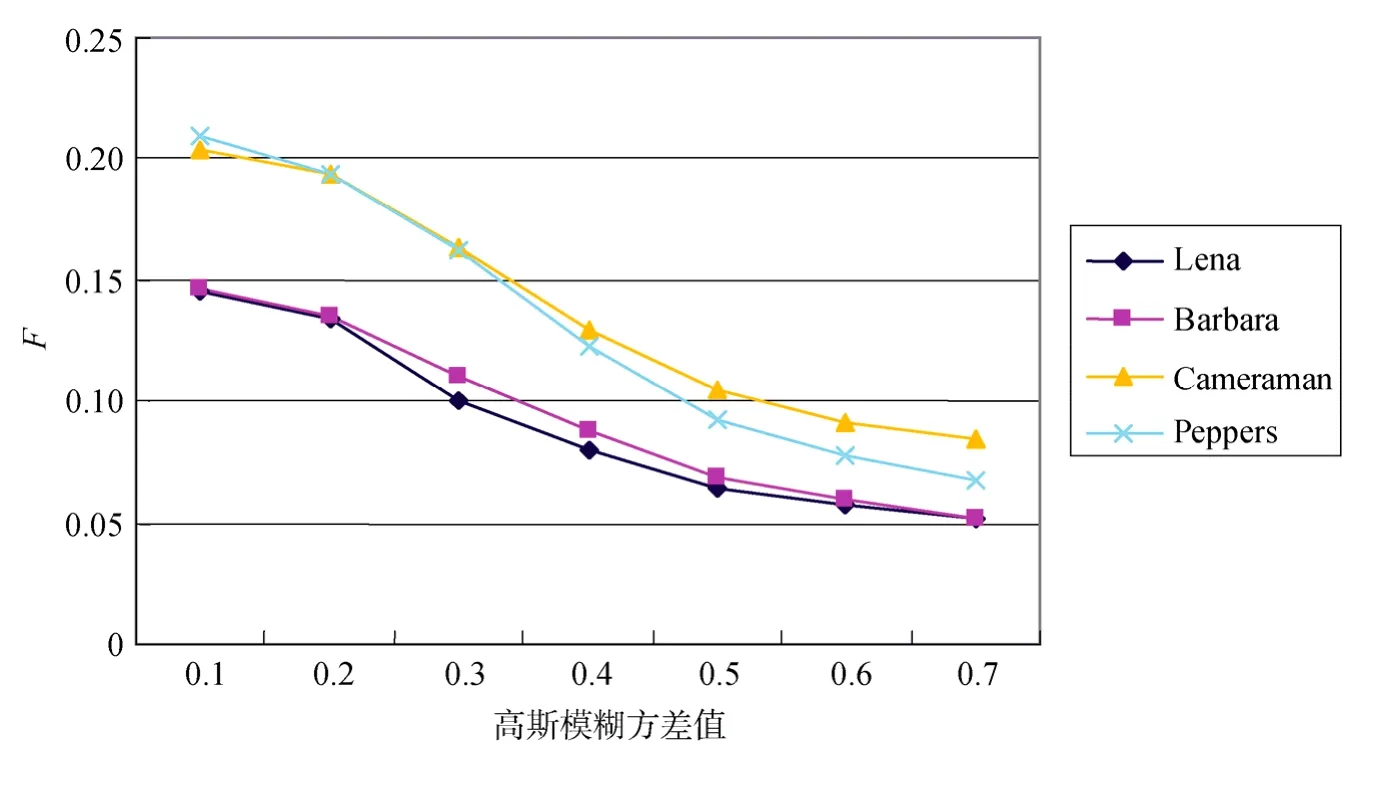
图5 高斯模糊图像的EMD清晰度拟合曲线Fig.5 The fitted curve of EMD definition of Gaussian blur images

图6为不同复原算法的效果图，算法A未知，该效果图由网站直接下载获取，算法B为基于理想边缘图像类推的复原算法。通过统计50个人对复原图像清晰度的主观评价，得出的结论是算法B复原效果好于算法A。为验证EMD清晰度与主观评价的一致性，表1列出了不同客观评价方法的计算数值。由表1可以看出EMD图像清晰度的数值与主观评价和SNR保持了良好的一致性，图像熵评价方法则出现偏差。

图6 不同算法复原遥感图像效果对比Fig.6 Recovery results of the remote sensing image w ith different algorithms

表1 遥感图像客观评价值对比Tab.1 Comparison of objective assessments of the above remote sensing images

5 结束语

本文在深入研究已有的灰度变化函数用于评价图像清晰度时存在片面性的基础上，结合经验模式分解后多层IMF图像的物理意义，构造了EMD图像清晰度参数，提出了一种全新的无参考图像清晰度评价方法。试验结果表明了该参数用于评价图像清晰度的有效性，可以针对模糊失真程度进行准确评价。但由于传统的 EMD方法对高频信息过于敏感，导致评价噪声失真的图像时将得出与主观评价不一致的结果，后续研究中将对EMD方法予以改进，使基于EMD的图像评价参数也适用于含有噪声失真的图像，扩大其应用范围。

References)

[1]周景超, 戴汝为, 肖柏华. 图像质量评价研究综述[J]. 计算机科学, 2008, 35(7): 1-4.ZHOU Jingchao, DAI Ruwei, XIAO Baihua. Overview of Image Quality Assessment Research[J]. Computer Science, 2008,35(7): 1-4. (in Chinese)

[2]马文坡. 卫星光学遥感系统优化设计与像质评价探讨[J]. 航天返回与遥感, 2007, 28(4): 23-27.MA Wenpo. Discussion on Optimal Design and Image Quality Evaluation of Satellite Optical Remote Sensing System[J].Spacecraft Recovery and Remote Sensing, 2007, 28(4): 23-27. (in Chinese)

[3]满益云, 陈世平, 刘兆军, 等. MTFC在光学遥感成像系统优化设计中的应用研究[J]. 航天返回与遥感, 2007, 28(4):39-47.MAN Yiyun, CHEN Shiping, LIU Zhaojun, et al. Study on MTF Compensation Application to the Optimization Design of Op-tical Remote Sensing Imaging System[J]. Spacecraft Recovery and Remote Sensing, 2007, 28(4): 39-47. (in Chinese)

[4]陈世平, 姜伟. 航天光学采样成像系统MTF的优化设计与MTFC[J]. 航天返回与遥感, 2007, 28(4): 17-22.CHEN Shiping, JIANG Wei. The MTF Optimal Design and MTFC for Spaceborne Optics[J]. Spacecraft Recovery and Remote Sensing, 2007, 28(4): 17-22. (in Chinese)

[5]朱孔凤, 姜威, 王端芳, 等. 一种新的图象清晰度评价函数[J]. 红外与激光工程, 2005, 34(4): 464-468.ZHU Kongfeng, JIANG Wei, WANG Duanfang, et al. New Kind of Clarity-evaluation-function of Image[J]. Infrared and Laser Engineering, 2005, 34(4): 464-468. (in Chinese)

[6]吴利明, 陶晓杰. 一种新的图象清晰度评价方法[J]. 仪器仪表用户, 2008, 15(6): 84-86.WU Lim ing, TAO Xiaojie. A New Kind of Definition Evaluation Function of Image[J]. Electronic Instrumentation Customer,2008, 15(6): 84-86. (in Chinese)

[7]王彪, 姜志国, 赵丹培. 遥感图像运动模糊恢复方法及评价标准研究[J]. 航天返回与遥感, 2009, 30(2): 18-25.WANG Biao, JIANG Zhiguo, ZHAO Danpei. Research on Technologies and Quality Evaluation for Restoring Remote Sensing Motion-blurred Image[J]. Spacecraft Recovery and Remote Sensing, 2009, 30(2): 18-25. (in Chinese)

[8]王鸿南, 钟文, 汪静, 等. 图像清晰度评价方法研究[J]. 中国图象图形学报, 2004, 9(7): 828-831.WANG Hongnan, ZHONG Wen, WANG Jing,et al. Research of Evaluation for Digital Image Definition[J]. Journal of Image and Graphics, 2004, 9(7): 828-831. (in Chinese)

[9]盖强, 殷福亮. 二维Hilbert_Huang变换的分解方法研究[J]. 电子与信息学报, 2006, 28(4): 610-613.GAI Qiang, YIN Fuliang. Study of Decomposition Method of 2-Dimension Hilbert-Huang Transform[J]. Journal of Electronics & Information Technology, 2006, 28(4): 610-613. (in Chinese)

[10]EI-Hadji Samba Diop, Radjesvarane A lexandre, Lionel Moisan. Intrinsic Nonlinear Multiscale Image Decomposition: A 2D Empirical Mode Decomposition-like Tool[J]. Computer Vision and Image Understanding, 2012, 116:102-119.