求解置换流水车间调度问题的布谷鸟算法

刘长平， 叶春明

（1.上海理工大学 管理学院，上海 200093；2.淮阴工学院 经济管理学院，淮安 223001）

置换流水车间调度问题（permutation flow shop scheduling problem，PFSP）是在流水车间调度问题约束的基础上，进一步增加所有工件在任一台机器上的加工顺序均相同的约束后形成的生产调度问题，对PFSP的调度优化可有效提高企业生产效益，但Garey等［1］早已证明机器数大于等于3的PFSP属于NP完全问题，尚无多项式计算复杂性的全局优化算法.因此，针对PFSP研究和开发高效的优化技术具有重要的实际意义和工程价值.综合现有文献，求解PFSP的方法主要有经典算法、构造型算法和智能优化算法.其中，经典算法（如分支定界法、动态规划法等）可求得问题的精确解，但受问题规模和计算复杂性的限制，只适于求解小规模问题.构造型算法（如NEH法、Rajendran法等）能够快速建立问题的调度解，但构造复杂，且通常解的质量较差，主要用于求解双机和三机PFSP.智能优化算法（如遗传算法［2］、蚁群算法［3］、粒子群算法［4］、蜂群算法［5］以及各种混合算法等）通过对邻域的不断搜索和当前解的持续改进，能够在可接受时间内以较大概率获得最优解或满意解，取得了较好的优化效果，在求解各种生产调度问题中获得了广泛应用.布谷鸟算法（cuckoo search，CS）是模拟自然界中布谷鸟寄生孵育雏鸟的生物行为发展而来的一种群智能优化算法，由Yang等［6］提出.该算法模型简单、可调参数少、收敛速度快，目前仅在函数优化领域得到应用［7－8］，在组合优化领域的特性和应用尚未进行研究.基于布谷鸟算法的优化机理和特点，针对置换流水车间调度问题的结构特性，本文应用该算法对置换流水车间调度问题进行求解，对其在组合优化领域的优化性能进行评估.仿真实验表明了该算法在离散空间也具有良好的进化机制，有利于拓展到对其它组合优化问题的求解.

1 置换流水车间调度问题描述

如果考核的调度指标为最大完工时间，此类PFSP用调度三元法可表示为其中，Fm为m台机器的流水车间调度；prmu表明所有工件在任一台机器上的加工顺序均相同；Cmax为最大完工时间.数学描述为［9］：令tjk，i表示工件jk在机器i上的加工时间（假设各工件的加工准备时间已包含在加工时间内），Cjk，i表示工件jk在机器i上的完工时间为所有排序的集合，加工过程满足不可中断约束、机器唯一性约束和工件唯一性约束，假设各工件按照机器1到m的顺序进行加工，则工件在各机器上的完工时间可以通过递归方程计算

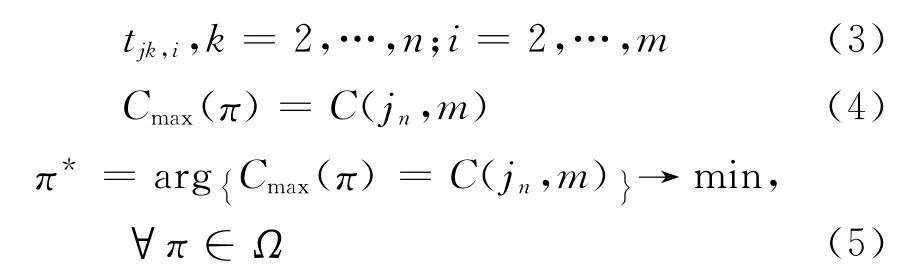
其中，式（1）～式（3）为计算完工时间的递归方程，式（4）为最大完工时间，式（5）为最小化最大完工时间所对应的调度方案，n表示工件数.

2 布谷鸟算法的优化机理

2.1 算法仿生原理

布谷鸟是典型的巢寄生鸟类，其巢寄生行为表现在：a.布谷鸟自己不筑巢也不孵卵，将卵寄生在宿主的鸟巢里，让其替自己孵化养育；b.布谷鸟在繁殖期寻找与孵化期和育雏期相似、雏鸟食性基本相同、卵形与颜色易仿的宿主；c.寄生时间上，布谷鸟多在宿主开始孵卵之前，乘宿主离巢外出时快速寄生产卵.宿主如果发现巢中的卵不是自己所产，会将“外来者”扔出或者弃巢另建新窝.因此，布谷鸟后代只能以一定概率得以孵化存活，概率大小取决于所选寄生鸟巢的状况.如果所选寄生宿主的卵形与颜色相近、孵化期和育雏期相似、雏鸟食性基本相同，则后代被孵化并得以存活的可能性就大些；反之，就小一些.

布谷鸟算法是模拟自然界中布谷鸟寄生孵育雏鸟的生物行为构造出的随机搜索算法，体现了自然的择优机制.其仿生原理是：将布谷鸟所选宿主鸟巢映射为搜索空间中的点，将搜索和优化过程模拟成布谷鸟搜寻和选择鸟巢的过程，用宿主鸟巢所处位置的优劣来代表孵育环境的好坏，进而代表待求解问题的适应度.将宿主鸟巢的择优过程类比为搜索和优化过程中用好的可行解取代较差可行解的迭代过程.和真实的寄生孵育行为相比，算法中做了一些假设：假设宿主鸟巢的数量是固定的，并且布谷鸟在一巢只产一卵；宿主鸟巢位置越好，布谷鸟后代孵化存活的几率越大.

2.2 算法的数学模型

布谷鸟寄生孵育雏鸟的生物行为可以用如下过程［6－7］进行模拟：

定义1 布谷鸟选择宿主鸟巢的位置更新式为

定义2 宿主发现“外来者”的概率为Pa，Pa大则布谷鸟后代孵化存活的概率小，反之则大.

算法实现优化的过程是：布谷鸟首先在解空间内随机选择一定数量的鸟巢并产卵，评估鸟巢优劣，找出当前最好的鸟巢，然后按照式（6）选择新的鸟巢产卵（保留当前最好鸟巢）.宿主若发现（概率为Pa）自己鸟巢中有“外来者”则放弃该鸟巢另建新巢，否则就接受更新位置后的鸟巢.布谷鸟对更新后的鸟巢进行评估，找出最佳鸟巢，若更优，则在当前最佳鸟巢中产卵.这样通过多次搜索和选择后，布谷鸟可以找到最好的鸟巢（最优位置），从而保证后代得以孵化存活.

3 置换流水车间调度问题求解

3.1 种群编码方式

PFSP属于典型的组合优化问题，应用布谷鸟算法求解PFSP首先需要构造合理的编码方式来表示调度问题的解.针对PFSP的特性，本文采用基于最小位置值规则的随机键编码方式［10］，将布谷鸟选择宿主鸟巢的一个连续位置向量Xi＝［xi，1，xi，2，…，xi，n］转换为机器上一个工件的加工顺序π＝（j1，j2，…，jn），从而可以计算鸟巢位置所对应调度解的适应度值.这种编码方式，保证了Xi→π得到的调度解均是可行解，同时无需修改布谷鸟算法的进化操作.

3.2 算法流程

综上所述，求解置换流水车间调度问题的布谷鸟算法流程如下：

a.初始化算法基本参数，布谷鸟选择宿主鸟巢数目m，发现概率Pa，步长因子α，搜索精度ε或最大搜索次数maxT；

b.布谷鸟随机选择鸟巢位置xi（i＝1，…，m），按照编码方式转换为工件加工顺序，计算各鸟巢适应度，找出当中前最佳鸟巢位置x＊；

c.根据式（6）更新鸟巢的空间位置xi；

d.产生随机数rand1，若rand1＞Pa，宿主放弃自己的鸟巢另建新巢，否则接受更新位置后的鸟巢；

e.对全部鸟巢进行评估，找出当前最佳鸟巢及所处位置，若优于以往最佳鸟巢则替换；

f.当满足搜索精度或达到最大搜索次数转g，否则转c，进行下一轮搜索；

g.输出最优值和对应调度方案.

算法的时间复杂度为O（mmaxT）.

4 仿真实验与分析

为了验证布谷鸟算法求解PFSP的性能，对算法没有采用任何改进策略，完全依靠算法自身进化机制来寻优.选择Car类［11］基准测试问题进行仿真测试，并与萤火虫算法（firefly algorithm，FA）［12］、粒子群算法（particle swarm optimization，PSO）［13］在离散空间的优化性能进行对比.

仿真环境：Windows XP操作系统，MATLAB R2010a编译软件，处理器主频2.4GHz，内存2GB.

算法参数设置为布谷鸟算法：发现概率Pa＝0.75，步长因子α＝1.0.萤火虫算法：光强吸收系数γ＝1.0，最大吸引度β0＝1.0，步长因子α＝0.2.粒子群算法：采用线性减少的惯性权重Wmax＝0.9，Wmin＝0.4.学习因子：C1＝C2＝1.4 962.这3种算法中群体数m＝25，最大搜索次数maxT＝500，每种算法独立运行10次，p代表测试问题类型，C＊表示对应调度问题的最小化完工时间，测试结果如表1所示.

表1 3种算法仿真测试结果Tab.1 Results of simulation tests for three algorithms

为对比算法的性能，采用了寻优成功率（success rate，SR）、最优相对误差（best relative error，BRE）、平均相对误差（average relative error，ARE）、最差相对误差（worst relative error，WRE）4项指标进行衡量.从测试结果可以看出，对于上述测试问题，CS均能找到已知下界值而且寻优成功率高于对应的FA和PSO算法，反映出CS具有良好的全局收敛性.从ARE和BRE指标来看，CS所求得调度解的质量远高于FA和PSO算法，显示出CS在离散空间具有优良的进化机制，而且CS求得ARE和BRE的值很小，表明CS算法对初始值具有较强的鲁棒性.从测试寻优曲线可以直观看出，对于Car3、Car5问题，FA与PSO均出现了早熟收敛，而CS收敛速度和收敛精度均高于对比算法，限于篇幅，只列出了有代表性的两幅图（如图1和图2所示）.

图1 Car3问题寻优进化曲线Fig.1 Optimization curve of Car3problem

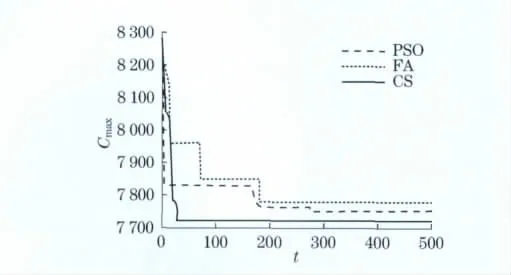
图2 Car5问题寻优进化曲线Fig.2 Optimization curve of Car5problem

5 结束语

布谷鸟算法通过模拟自然界中布谷鸟寄生孵育雏鸟的生物学特性，利用进化方式来实现多智能体的行为以达到优化目的，体现了自然选择的择优机制.本文针对最小化最大完工时间的置换流水车间调度问题，应用布谷鸟算法进行求解，测试和对比结果验证了该算法求解置换流水车间调度问题的有效性和优越性，在生产调度优化领域展现出良好的应用前景.

［1］Garey M R，Johnson D S，Sethi R.The complexity of flow shop and job shop scheduling［J］.Mathematics of Operations Research，1976，1（2）：117－129.

［2］朱夏，李小平，王茜.基于总空闲时间增量的无等待流水调度混合遗传算法［J］.计算机研究与发展，2011，48（3）：455－463.

［3］刘延凤，刘三阳.多构造蚁群优化求解置换流水车间调度问题［J］.计算机科学，2010，37（1）：222－224.

［4］田野，刘大有.求解流水车间调度问题的混合粒子群算法［J］.电子学报，2011，39（5）：1087－1093.

［5］李修琳，鲁建厦，柴国钟，等.混合蜂群算法求解柔性作业车间调度问题［J］.计算机集成制造系统，2011，17（7）：1495－1500.

［6］Yang X S，Deb S.Cuckoo search via Lévy flights［C］∥Proceedings of World Congress on Nature ＆Biologically Inspired Computing（NaBIC2009），India：IEEE Publications，2009：210－214.

［7］Yang X S，Deb S.Engineering optimization by cuckoo search［J］.International Journal of Mathematical Modelling and Numerical Optimisation，2010，1（4）：330－343.

［8］王凡，贺兴时，王燕.基于高斯扰动的布谷鸟搜索算法［J］.西安工程大学学报，2011，25（4）：565－569.

［9］Michael P.调度：原理、算法和系统［M］.2版.北京：清华大学出版社，2007.

［10］Tasgetren M F，Sevkli M，Liang Y C，et al.Particle swarm optimization algorithm for permutation flowshop sequencing problem［J］.Lecture Notes in Computer Science，2004，3172：382－389.

［11］Carlier J.Scheduling with disjunctive constraints［J］.Operations Research，1978，12（4）：333－350.

［12］刘长平，叶春明.一种新颖的仿生群智能优化算法：萤火虫算法［J］.计算机应用研究，2011，28（9）：3295－3297.

［13］Shi Y，Eberhart R.A Modified Particle Swarm Optimizer［C］∥Proceedings of IEEE International Conference on Evolutionary Computation，Anchorage：IEEE Publications，1998：69－73.