基于粒子群的多目标多执行模式项目调度
2013-10-10叶春明
周 蓉, 叶春明
(上海理工大学 管理学院,上海 200093)
在工程项目调度中保持工期、成本、质量以及资源的均衡控制是构成项目建设总目标的关键因素,关系到整个工程的成败.为了实现工程项目的总效益,需要对工程项目所要求的质量、所规定的工期、所批准的费用等各个目标进行全方位的协调,因此建立一套科学有用的多目标多模式项目调度综合优化模型十分有必要.
目前,解决工程项目优化问题的基本方法主要是网络计划技术,其在解决工程费用、工期、资源等单目标优化方面带来了极大方便.然而,现代的工程项目仅仅考虑单目标的优化是远远不行的.因此,许多专家希望引入最优化技术来研究工程项目多目标优化问题.如王首续[1]、骆刚等[2]将遗传算法引入工程项目优化问题,通过选择、变异、杂交等操作,实现工程项目多目标优化.刘永淞[3]则采用动态规划法(DP)研究工程项目优化问题.杨湘等[4]则应用模糊数学和遗传算法来解决工程项目资源均衡优化问题.
粒子群算法(particle swarm optimization,PSO)是一种智能演化计算技术[5],系统初始化为一组随机解,通过迭代搜索最优值.与其它算法比较,PSO的优势在于算法简单和容易实现,同时又有深刻的智能背景,既适合科学研究,又特别适合工程应用.因此,PSO一经提出,立刻引起演化计算领域学者们的广泛关注,并在短短的几年时间里出现大量的研究成果,形成了一个研究热点[6].
因此,本文主要以工程项目多目标多执行模式优化模型为研究对象,对项目调度所涉及的重要目标建立综合优化模型,并将粒子群算法引入工程项目优化领域,最终实现工程项目的工期、成本、质量以及资源的均衡性达到合理的配置.
1 项目优化模型建立
1.1 模型假设
根据实际情况,对工程项目中工期、成本、质量以及资源等给予如下假设[7]:
a.合理工期是工程项目在正常的条件情况下,使项目的投资方和各参建单位均获得满意的经济效益的工期.
b.工程总成本是工程的直接成本与间接成本之和.
c.工程总质量由各个单项任务的质量加权平均得到.
d.本文的工期指工程项目的合理工期.
e.本文直接成本主要指各类资源使用成本;间接成本主要指运输成本.
f.工程质量与具体活动的施工组织方式有关,施工组织方式不同,单项工程的质量不同.
本文问题具体可描述如下:一个工程中包含J项任务,规定任务j在其全部紧前任务i(i∈Pj,Pj为任务j的紧前任务集)完成之前不能开始.任务1是唯一最早开始的任务,任务J是唯一最晚完成的任务,均为虚拟任务,即不消耗资源且执行时间为0,表示整个工程的开始和结束.又规定任务j(j=1,2,…,J)必须选择Mj种执行模式之一执行,且在执行过程中不能中断或改变执行模式.在第m(1≤m≤Mj)种模式下任务j执行时间为djm.根据各任务在各执行模式下的最短执行时间,并利用传统的时间参数计算方法,可计算出各任务的最早、最晚完成时间窗口[EFj,LFj].
同时,引进如下决策变量:

1.2 项目工期模型
工程项目的工期优化模型为
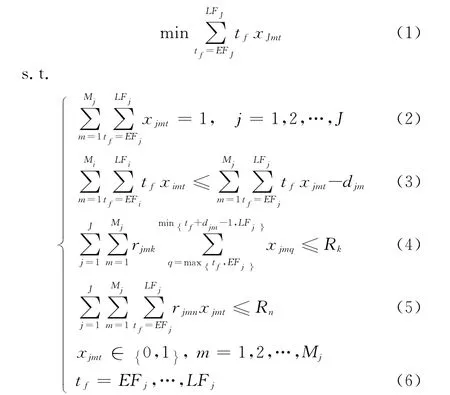
1.3 项目成本模型
工程项目的成本优化模型为
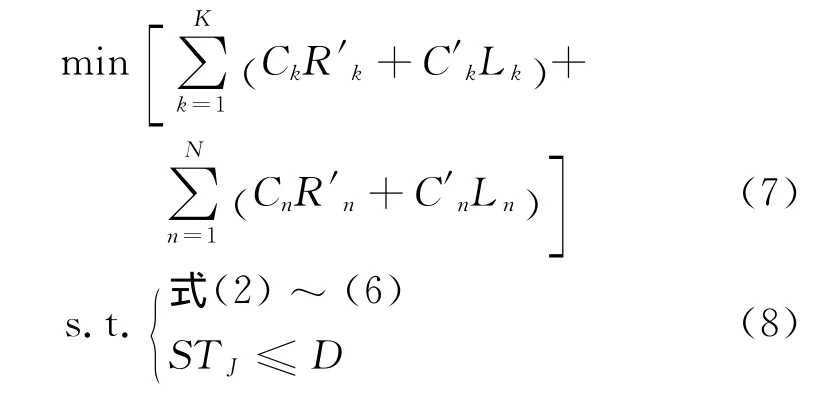
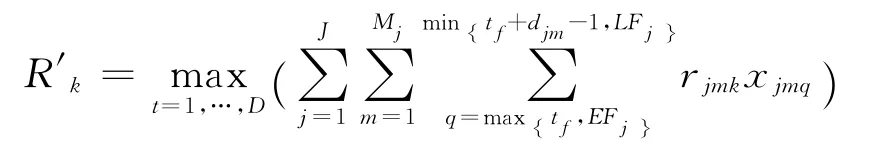
指整个工期内可更新资源k的最大消耗水平;
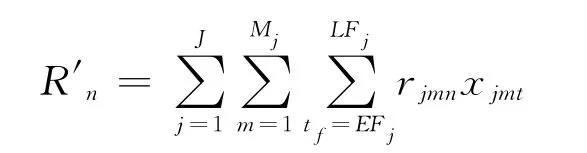
为整个项目不可更新资源n的消耗量;
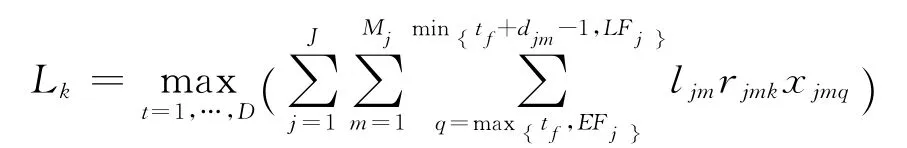
定义为整个工期内可更新资源k的最大路径运输量,即任务j在m模式下的路径长度ljm与资源需求量rjmk的乘积;
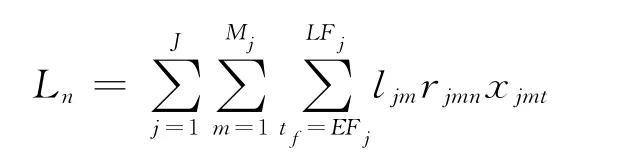
同理定义为整个项目不可更新资源n的最大路径运输量.
1.4 项目资源均衡模型
资源均衡优化就是在工程项目执行过程中,使资源计划使用量在整个工期内趋于均衡[8].在编制工程网络计划时,要对工作的实际时间进行适当地调整,减少资源使用量的高峰与低谷的差值,即达到资源方差值最小.目标函数如下
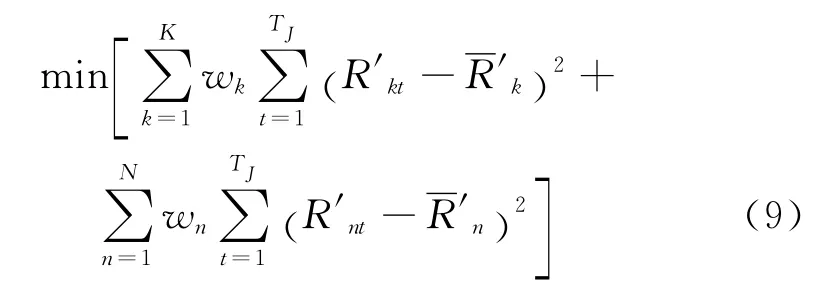
s.t. 式(2)~(6)
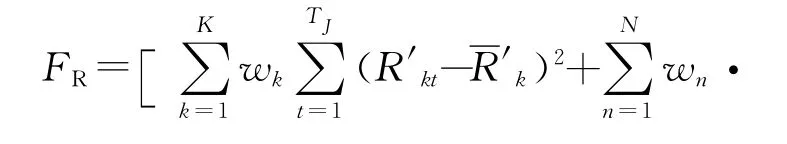
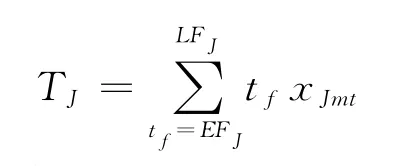
指项目的完成时间;

为项目中在时段t可更新资源k的消耗总量;
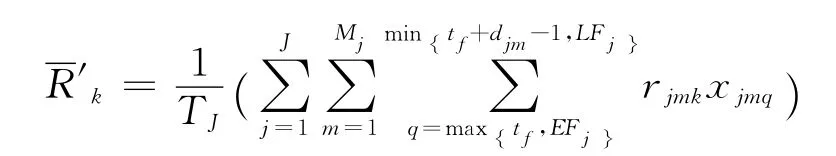
表示可更新资源k在整个项目工期内的平均资源消耗水平;
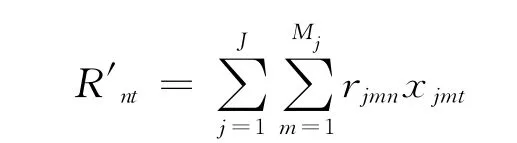
为项目中在时段t不可更新资源n的消耗总量;
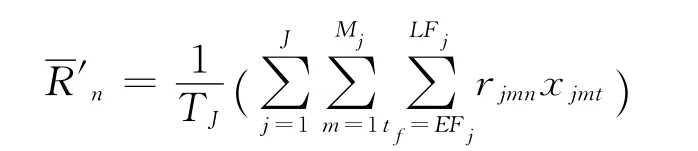
则表示不可更新资源n在整个项目工期内的平均资源消耗水平.
1.5 项目质量模型
考虑到工程质量的特殊性,这里对工程质量进行重新定义和假设.参照文献[9-12],本文在基本模型建立的基础上,采用专家估测法对工程质量进行评分,并确定单个活动在工程中所占的权重.具体目标函数如下

FQ=为项目质量目标函数,式(10)表示质量最优.式中,wj指任务j的权重;qjm指任务j在m模式下的质量得分.
1.6 多目标优化模型建立
为了能够对工程项目进行综合优化,这里将前面的工期、成本、资源和质量各优化目标函数加权求和,建立多目标优化函数
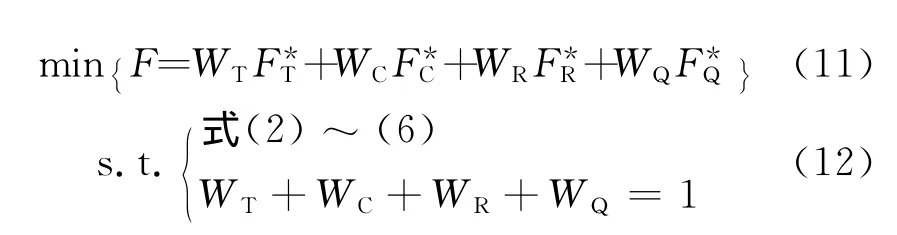
式中,WT、WC、WR、WQ分别为各个目标函数的权重;由于各个模型的目标函数值具有不同的单位和量纲,在进行多目标决策之前先将这些目标无量纲化,即仅用数值的大小来反映各目标属性值的优劣,式中的则是将各目标函数通过无量纲化所得到的,具体为
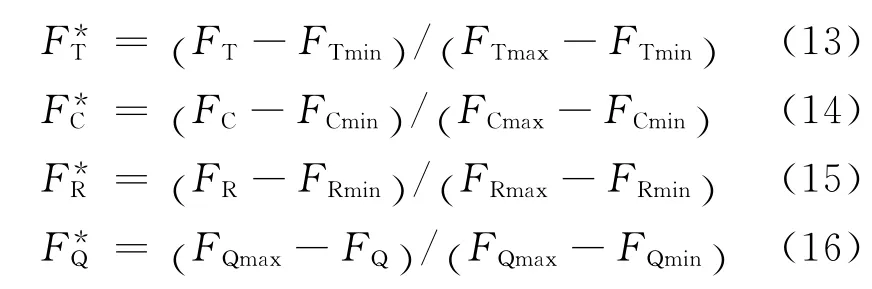
其中工期、成本、资源及质量各目标函数分别得到的最大、最小值为FTmax,FTmin,FCmax,FCmin,FRmax,FRmin和FQmax,FQmin.
2 粒子群优化算法
2.1 算法思想
粒子群优化算法是由Eberhart博士与Kennedy博士发明的一种新的全局优化进化算法.该算法源于对鸟类捕食行为的模拟[6].粒子群优化算法首先初始化一群随机粒子,然后通过迭代找到最优解.在每一次迭代中,粒子通过跟踪两个“极值”来更新自己.一个是粒子本身所找到的最优解,即个体极值pbest.另一个是整个种群目前找到的最优解,称之为全局极值gbest.粒子在找到上述两个极值后,就根据下面两个公式来更新自己的速度与位置[6]:
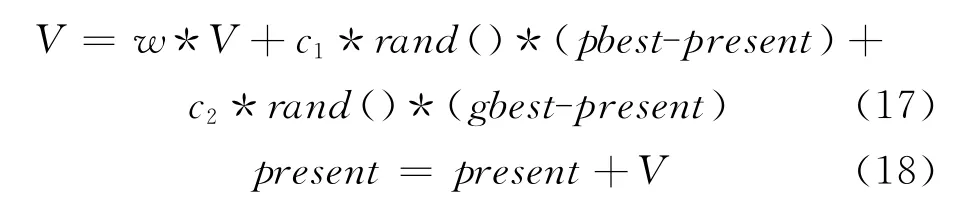
式中,V是粒子的速度;present是粒子的当前位置;rand()*是(0,1)之间的随机数;c1和c2被称作学习因子.通常,c1=c2=2,w是加权系数,取值在0.1~0.9之间.
根据上述公式,粒子最终飞至解空间中最优解所在的位置,搜索过程结束.最后输出的gbest就是全局最优解.在更新过程中,粒子每一维的最大速率被限制为Vmax,粒子每一维的坐标也被限制在允许范围之内.
2.2 算法流程与步骤
粒子群算法步骤如下[13]:
步骤1 初始化群体规模为M的粒子群(在控制范围内随机设定位置和速度);
步骤2 计算每个粒子的适应值f(p),p为粒子所处的位置;
步骤3 将每个粒子适应值与其经历过的最好位置pbest作比较,如果f(pi)<f(pbesti),则f(pbesti)=f(pi);
步骤4 将每个粒子适应值与全局极值gbest作比较,如果f(pi)<f(gbest),则f(gbest)=f(pi);
步骤5 根据粒子群算法的进化方程,更新速度和位置;
步骤6 若到达最大迭代次数G,输出结果;否则,返回步骤2.
标准PSO算法流程如图1所示[14].

图1 PSO算法流程图Fig.1 PSO procedure
2.3 粒子群算法编码
2.3.1 粒子编码与初始化
在多执行模式的项目调度过程中,需要选择一个可行的执行模式和调度顺序.因此,本文算法中有两种类型的粒子:模式粒子和优先级粒子.其中,模式粒子用以选择执行模式,优先级粒子用以选择各个任务的调度顺序.这两种粒子数量相同,组合形成了一个调度方案.
粒子群的搜索空间维度表示项目中的任务数,总数为J,模式粒子xim每个维度的值ximj都是随机值,大小不超过其对应的任务的可选模式总数,这个值表示任务j所选择的模式.优先级粒子yim每个维度的值yimj都是[0,1]的随机实数,这个值的大小表示选择m模式的任务j调度的优先顺序,值越大越优先调度.为方便理解和计算,取虚拟开始任务的优先值为1,虚拟结束任务的优先值为0,其余任务都在(0,1)中取随机实数.经过简单的降序排序后就得到一个调度顺序,但是这个调度顺序可能不符合逻辑关系约束,即紧后任务的优先值可能大于其紧前任务的值,所以在生成一个调度顺序后,需要加入一个逻辑关系判断程序,以剔掉不符合要求的粒子.
2.3.2 调度生成方式
基于优先规则的调度生成方式可分为两种:串行调度方案(serial scheduling scheme,SSS)和并行调度方案(parallel scheduling scheme,PSS)[15],本文采用的是串行调度方案.
串行调度方案的主要思路是:根据已经确定的调度顺序,按顺序加工,某个任务j的实际开始时间在其最早开始时间EFj与最晚开始时间LFj之间,在程序设计时,只需要判断在EFj和LFj之间,哪个时刻首先满足该任务的资源消耗量小于或等于该时刻的资源剩余总量,这个时刻便是该任务的实际开始时间Tf.依此类推,最后得到该调度顺序各个任务的实际开始时间、工期和成本等一系列目标值,然后通过适应度函数计算最优适应值.
2.3.3 粒子更新方式
粒子采用式(17)和式(18)对粒子速度和位置进行更新.更新后,如果模式粒子ximj<1,则ximj=1;如果ximj>M,则ximj=M.如果优先级粒子yimj≥1或者yimj≤0,yimj=rand.如果Vimj>1,则Vimj=1;如果Vimj<-1,则Vimj=-1.
3 应用实例
以国际标准问题库中的J1015-5.SM为测试问题,同时以实际项目经验所提供的基本数据为基础,应用基本粒子群算法求解上述模型下的多目标项目调度问题.作业及资源等信息如表1、表2(见下页)所示.
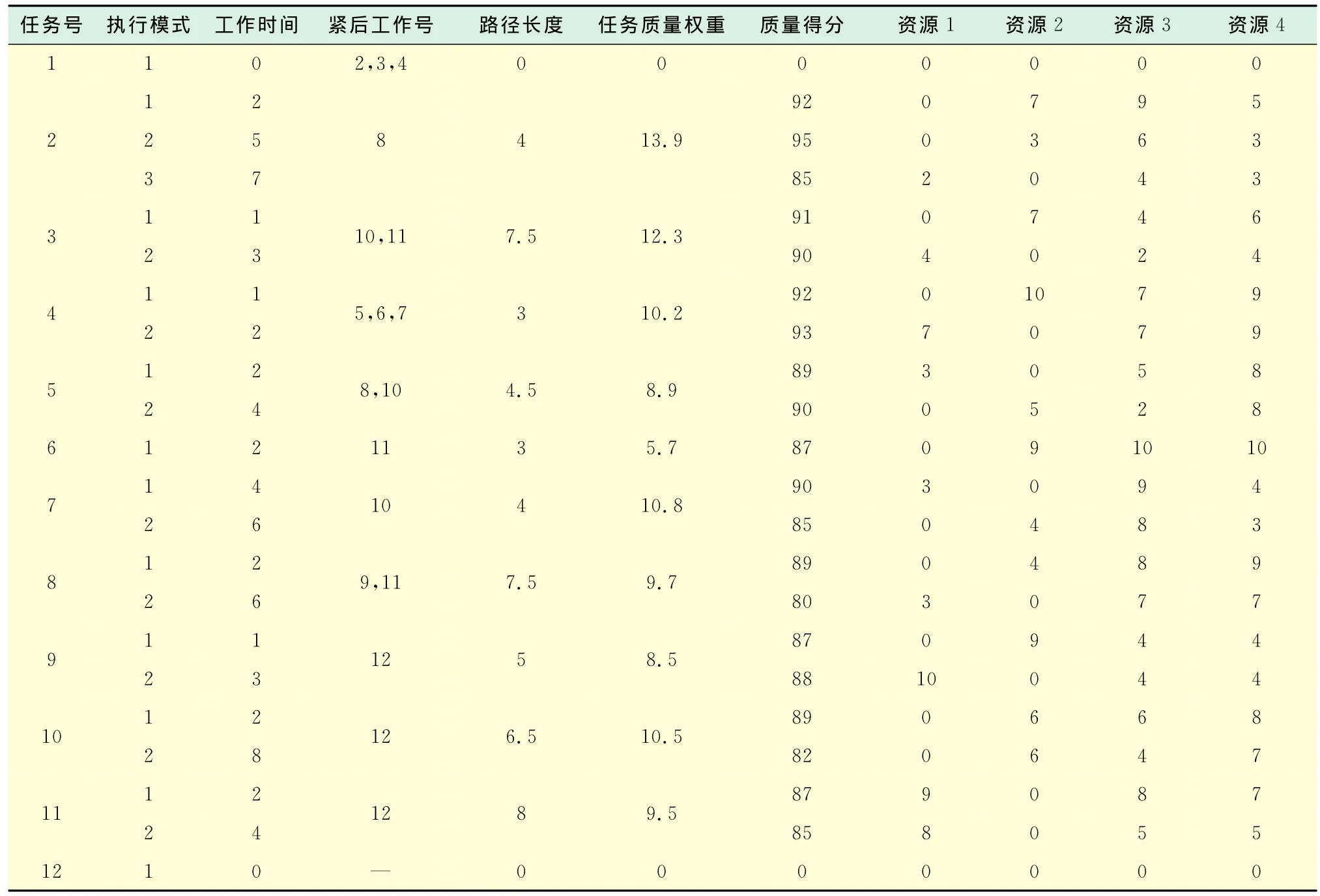
表1 作业信息表Tab.1 Operation information
同时,规定每单位数量资源运输单位长度所需成本为50;四大目标函数权重分别为WT=0.4,WC=0.25,WR=0.15,WQ=0.2.根据表1给出的逻辑关系,绘制出本项目的单代号网络图,如图2(见下页)所示.
这里采用Matlab 7.0对以上算法编程,算法参数设置:学习因子c1=c2=2,由于该问题只有12个任务,属于比较简单的调度问题,所以种群规模和进化次数不用设置的太大,本文中设定种群规模M=20,进化次数Gmax=500;粒子群算法迭代运行次数为G=500;w取惯性权重,取值w=wmax-(wmax-wmin)/Dmax,wmax,wmin分别取0.9和0.4.通过500次迭代运算得到了如表3所示的结果.
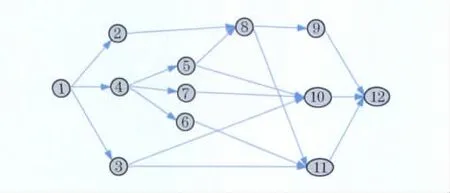
图2 项目网络图Fig.2 Project network diagram

表3 单目标与多目标运行结果比较Tab.3 Comparison between single-target & multi-target running results
同时,可以得到该多目标模型下最优方案的具体模式选择情况以及任务对应的调度顺序,如表4所示.
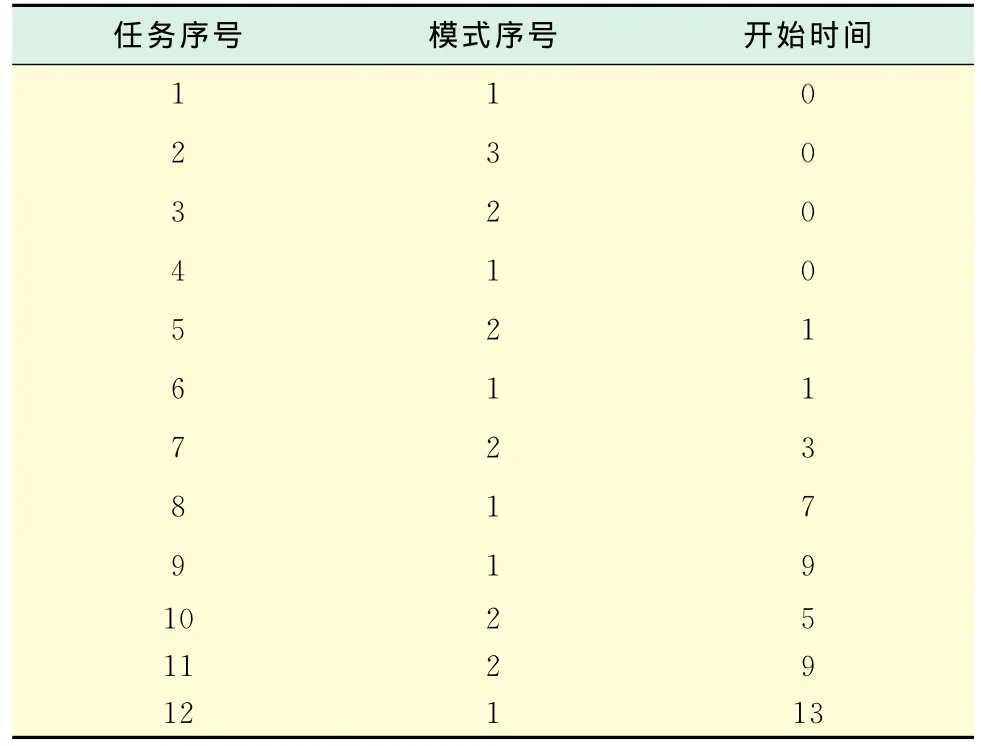
表4 最优方案任务执行信息表Tab.4 Details of the optimaldecision
通过500次进化运算,基本达到收敛性效果,计算平均运行时间为10min,达到平均最优值的比例为98.9%.同时,得到图3的多目标优化函数在此算例下的平均最优适应值曲线,即收敛图.由此可以看出,粒子群算法在求解该项目调度问题时方差较小,结果比较稳定.
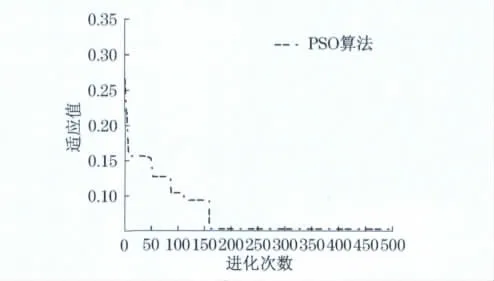
图3 算例收敛图Fig.3 Convergence of the case
4 结束语
本文提出在进行项目优化问题求解时,将控制目标有效地结合统一,形成一个综合、科学、有效的数学模型,这种思想是解决实际问题的根本和最优化设计成败的关键.
本文建立了工期—成本—资源均衡—质量的优化模型,并将各目标函数加权求和,采用单目标优化技术求解多目标优化问题,并采用粒子群优化算法求解工程项目多目标问题,能较好地平衡全局与局部搜索能力,保持种群的多样性,避免早熟.
项目实例验证结果表明,该综合优化模型具有较好的适用性,粒子群优化算法在求解该多目标项目优化模型问题时具备可行性,并且基本达到了预期理想的结果.
[1]王首续,周学林.遗传算法优化施工网络计划的多种资源均衡[J].重庆交通学院学报,2001,20(2):39-45.
[2]骆刚,刘尔烈,王健.遗传算法在网络计划资源优化中的应用[J].天津大学学报,2004,37(2):179-183.
[3]刘永淞.DP法工期优化[J].湘潭大学学报,2002,24(1):106-108.
[4]杨湘,张连营.工程项目工期——成本综合模糊优化[J].土木工程学报,2003,36(3):46-50.
[5]刘寅,马良,黄珏.基于模糊粒子群算法的非线性函数优化[J].上海理工大学学报,2012,34(4):314-322.
[6]Kennedy J,Eberhart R C.Particle swarm optimization[C]∥IEEE International Conference on Neural Networks,Perth,1995.[7]与科学王维博,冯 全源.基于改进粒子群算法的工程项目综合优化[J].西南交通大学学报,2011,46(1):76-83.
[8]齐东海,宋向群.工程项目进度管理[M].大连:大连理工大学出版社,2001.
[9]王健,刘尔烈,骆刚.工程项目管理中工期成本质量综合均衡优化[J].系统工程学报,2004,19(2):148-153.
[10]杨耀红,汪应洛,王能民.工程项目工期成本质量模糊均衡优化研究[J].系统工程理论与实践,2006,26(7):114-117.
[11]Kaheled E, Amr K. Time-cost-quality-trade-off analysis for highway construction[J].Journal of Construction Engineering and Management,2005,131(4):477-485.
[12]Afshar A,Kaveh A,Shoghli O R.Multi-objective optimization of time-cost-quality using multicolonyant algorithm [J].Asian Journal of Civil Engineering(Building and Housing),2007,8(2):113-124.
[13]陈志勇,杜志达,周华.基于微粒群算法的工程项目资源均衡优化[J].土木工程学报,2007,40(2):93-96.
[14]杨维,李歧强.粒子群算法综述[J].中国工程科学,2004,6(5):87-95.
[15]Kolisch R.Serial and parallel resource-constrained project scheduling methods revisited:theory and computation[J].European Journal of Operational Research,1996,90(2):320-333.
