非线性项变号的分数阶微分方程边值问题正解的存在性

王 淑， 贾 梅， 祁卫杰

（上海理工大学 理学院，上海 200093）

1 问题的提出

随着科学技术的发展，分数阶微分方程在扩散和运输理论［1］、高分子材料的解链［2］及非牛顿流体力学［3］等诸多领域得到了广泛的应用.随着应用背景的不断拓宽，进一步促进了分数阶微分方程的理论研究.

近年来，分数阶微分方程两点边值问题［4－5］、三点边值问题［6］、多点边值问题［7］及积分边值问题［8－9］正解的存在性研究已取得了很多成果，然而，现有文献大多是在非线性项不变号情况下研究边值问题正解的存在性.目前，对于非线性项变号的整数阶微分方程边值问题正解存在性的研究已很多［10－12］，但对非线性项变号的分数阶微分方程边值问题正解存在性的研究较少.

本文研究非线性项变号的分数阶微分方程边值问题

正解的存在性，其中，Dα为Caputo分数导数，2＜α＜3，λ＞0，f∶［0，1］×R→R是连续函数，a，b为常数.利用锥拉伸锥压缩不动点定理，得到了分数阶微分边值问题（1）正解的存在性定理，所得结论突显了参数在不同范围内对正解存在性的影响.

2 预备知识

定义1［13］函数h∶（0，＋∞）→R的α＞0阶积分是

其中，右边是在（0，＋∞）上逐点有定义的.

定义2［13］函数y∶（0，＋∞）→R的α＞0阶Caputo微分为

其中，n＝［α］＋1，［α］代表α的最大整数部分；右边是在（0，＋∞）上逐点有定义的.

记I＝［0，1］，E＝C（I）表示［0，1］上的连续函数全体，定义

为方便起见，假设以下条件成立：

（H1）f∈（［0，1］×R，R），对任意（t，u）∈［0，1］×R，存在M＞0，使得f（t，u）≥－M.

对任意的y∈C（I），首先考虑边值问题

引理1［8］假设（H0）成立，则边值问题（2）存在唯一解

其中

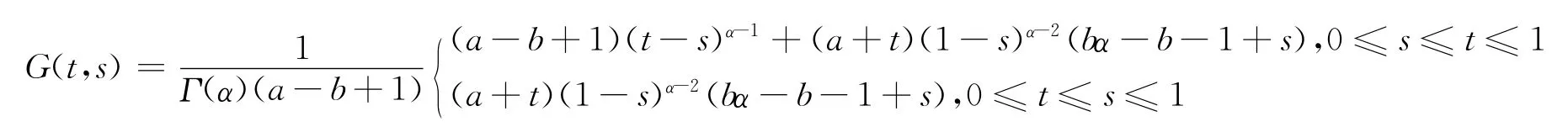
引理2 设（H0）成立，则函数G（t，s）具有下列性质：

a.G（t，s）≥0，（t，s）∈I×I；

b.G（0，s）≤G（t，s）≤G（1，s），（t，s）∈I×I；

c.对任意的 （t，s）∈I×I，有G（0，s）≥γG（1，s）.

证明 因为G（t，s）是关于t单调递增的函数，a和b显然成立.

因为

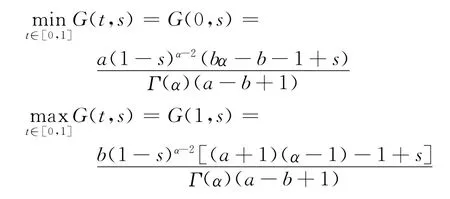
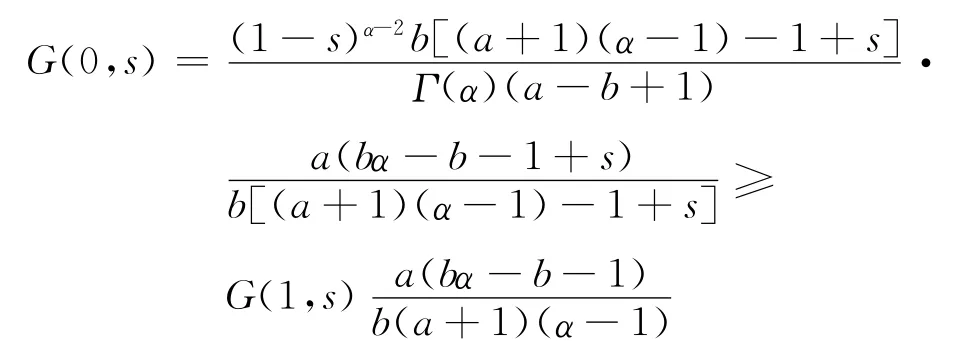
所以，G（0，s）≥γG（1，s）.

证毕.

引理3 设（H0）成立，对任意t∈I，y（t）≥0，则边值问题（2）的解u满足且u是单调递增的正解.

证明 由引理1和引理2可得，对任意t∈［0，1］，有

故

由于G（t，s）关于t是单调递增的，所以，u是单调递增的.

证毕.

如果y（t）≡1，则边值问题（2）变为

引理4 设（H0）成立，则边值问题（3）存在唯一正解使得对任意的t∈［0，1］，有 0＜证明由引理1和引理3可 得是边值问题（3）的唯一单调正解.根据引理2得

所以，对任意的t∈ ［0，1］，有

证毕.

令g（t，u）＝f（t，u）＋M，ω（t）＝（t），则当（H1）成立时，对任意（t，u）∈ ［0，1］× R，有g（t，u）≥0.

现考虑边值问题

引理5 设（H0）和（H1）成立，那么，u是边值问题（1）的一个正解的充分必要条件是＝u＋ω为边值问题（4）的一个正解，且对任意的t∈［0，1］，有¯u（t）≥ω（t）.

证明 如果u是边值问题（1）的一个正解，那么

则

因为，u（t）是正解，所以，易证（t）满足边界条件，因此是边值问题（4）的一个正解.

证毕.

引理6（锥拉伸锥压缩不动点定理）［14］设E是Banach空间，K⊂E，K为E中的一个锥，且Ω1和Ω2是E中的有界开集，θ∈Ω1⊂⊂Ω2，A∶K∩（＼Ω1）→K全连续的，如果满足下列条件之一：

a.‖Au‖≤‖u‖，u∈K∩∂Ω1，‖Au‖≥‖u‖，u∈K∩∂Ω2；

b.‖Au‖≥‖u‖，u∈K∩∂Ω1，‖Au‖≤‖u‖，u∈K∩∂Ω2.

那么，A在K∩（＼Ω1）中必有不动点.

定义映射A∶K→E，

引理7 设（H0）和（H1）成立，那么，则映射A∶K→K是全连续的.

证明 由引理3易得A（K）⊂K.

对任意的S⊂K，且S有界，则存在m0＞0，对任意的u∈S，有‖u‖≤m0.记

由于G（t，s）在［0，1］×［0，1］上连续，所以，G（t，s）在［0，1］×［0，1］上一致连续.因此，对任意的ε＞0，存在t1，t2，s1，s2∈［0，1］，当时，有

则

所以，A（S）是等度连续的.

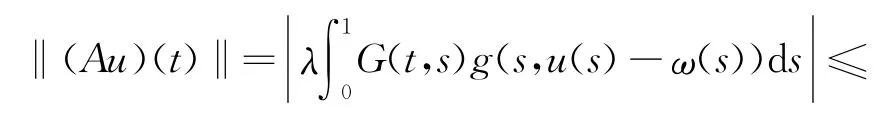
对任意的t∈［0，1］成立，所以，A（S）是一致有界的.

因此，根据Arzela－Ascoli定理可得A（S）是列紧的，从而A在S上是紧的.

在K中任取一个收敛数列｛un｝且有un→u，n→∞，所以，由g的连续性可得

而对任意t∈［0，1］，可得

所以

由Lebesgue控制收敛定理可得

因此，A是连续的，又因A是紧算子，所以，A是全连续的.

证毕.

3 主要结果

记

定理1 设（H0）和（H1）成立，且满足

则存在常数λ＊＞0，使得当λ∈（0，λ＊）时，边值问题（1）至少有一正解.

证明 对任意的r＞0，令

由条件

可得

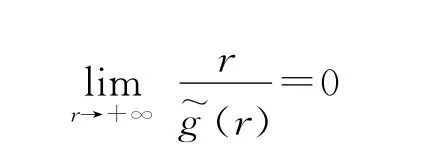
所以，存在常数R1＞0，使得

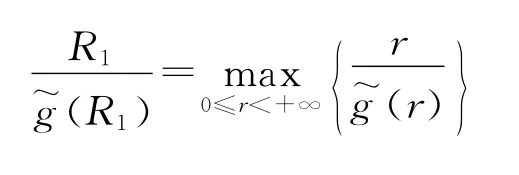
对任意λ∈（0，λ＊），u∈K∩∂Ω1，有u（t）≥，且u（t）－ω（t）满足

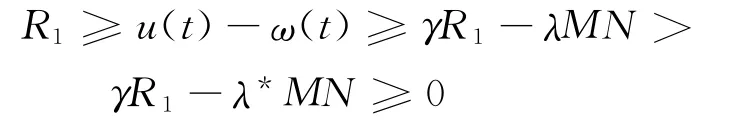
因此，由式（5）可得

所以，对任意u∈K∩∂Ω1，有‖Au‖≤‖u‖.

存在＞R1，使得对任意的t∈［0，1］，当u≥时，有g（t，u）≥ξu.令

对任意u∈K∩∂Ω2，有‖u‖＝R2，且对任意t∈［0，1］，u（t）≥γ‖u‖ ＝γR2≥，所 以，g（t，u（t））≥ξu（t）.

因为，对任意t∈［0，1］，

所以

因此

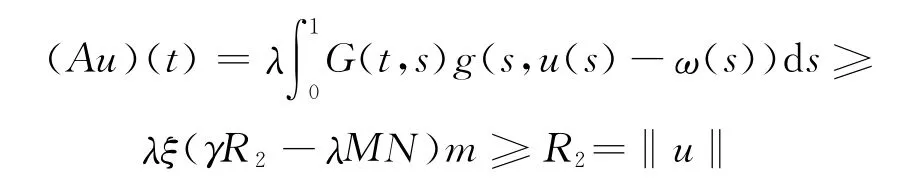
由此可得，对任意u∈K∩∂Ω2，有‖Au‖≥‖u‖.

根据锥拉伸锥压缩不动点定理可知，算子A有一个不动点u，所以，u为边值问题（4）的正解，满足R1≤‖u‖≤R2，且对任意t∈［0，1］，

由引理5可得，u（t）－ω（t）是边值问题（1）的一个正解.

证毕.

定理2 设（H0）和（H1）成立，且满足

则存在常数λ＊＞0，使得当λ∈（λ＊，＋∞）时，边值问题（1）至少有一正解.

所以，g（t，u（t）－ω（t））≥η.因此

由此可得，对任意u∈K∩∂Ω1，有‖Au‖≥‖u‖.

因为

则对任意u∈K∩∂Ω2，t∈［0，1］，满足u（t）≥γ‖u‖＝γR2.

因为，u（t）－ω（t）≥γR2－λMN≥~R2，所以

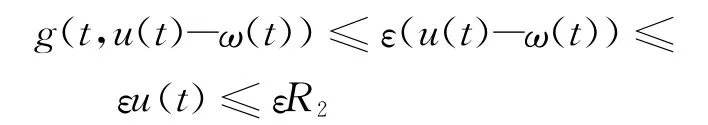
那么，对任意t∈［0，1］，

由此可得，对任意的u∈K∩∂Ω2，有‖Au‖≤‖u‖.

根据锥拉伸锥压缩不动点定理可知，算子A有一个不动点u，所以，u为边值问题（4）的解，满足R1≤‖u‖≤R2，且对任意的t∈［0，1］，

由引理5可得，u（t）－ω（t）是边值问题（1）的一个正解.

证毕.

4 应用实例

考虑边值问题

这里a＝b＝2，α＝5／2，对任意的t∈［0，1］，u∈R，有

从而易得

因为

所以，存在常数R1＞0，使得

经计算得

从而

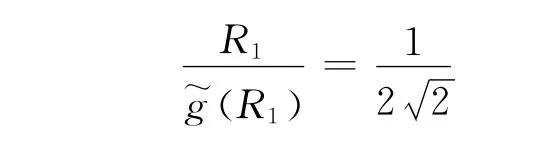
易证（H0）和（H1）成立.由定理1可得，当λ∈时，边值问题（6）至少存在一个正解.

［1］同登科，王瑞和，杨河山.管内非Newton流体分数阶流动的精确解［J］.中国科学G辑，2005，35（3）：318－326.

［2］Eidelman S D，Kochubel A N.Cauchy problem for fractional diffusion equations［J］.Journal of Differential Equation，2004，199（2）：211－255.

［3］徐明瑜，谭文长.广义二阶流体分数阶反常扩散速度场、应力场及涡旋层的理论分析［J］.中国科学A辑，2001，31（7）：626－638.

［4］Bai Z B，Lu H S.Positive solutions for boundary value problem of nonlinear fractional differential equation［J］.Journal of Mathematical Analysis and Applications，2005，311（2）：495－505.

［5］Goodrich C S.Existence of a positive solution to a class of fractional differential equations［J］.Applied Mathematics Letters，2010，23（9）：1050－1055.

［6］Bai Z B.On positive solutions of a nonlocal fractional boundary value problem ［J］.Nonlinear Analysis，2010，72（2）：916－924.

［7］Salem H A H.On the fractional order m－point boundary value problem in reflexive Banach spaces and weak topologies［J］.Journal of Computational and Applied Mathematics，2009，224（2）：565－572.

［8］金京福，刘锡平，窦丽霞，等.分数阶微分方程积分方程边值问题正解存在性［J］.吉林大学学报（理学版），2011，49（5）：823－828.

［9］Jia M，Liu X P.Three nonnegative solutions for fractional differential equations with integral boundary conditions［J］.Computers and Mathematics with Applications，2011，62（3）：1405－1412.

［10］Li G S，Liu X P，Jia M.Positive solutions to a type of nonlinear three－point boundary value problem with sign changing nonlinearities［J］.Computers and Mathematics with Applications，2009，57（3）：348－355.

［11］Wu Y Y，Zhao Z Q.Positive solutions for third－order boundary value problems with change of signs［J］.Applied Mathematics and Computation，2011，218（6）：2744－2749.

［12］Guo Y P，Tian J W.Two positive solutions for second－order quasilinear differential equation boundary value problems with sign changing nonlinearities［J］.Journal of Computational and Applied Mathematics，2004，169（2）：345－357.

［13］Podlubny I.Fractional differential equations，mathematics in science and engineering［M］.New York：Academic Press，1999.

［14］郭大钧，孙经先，刘兆理.非线性常微分方程泛函方法［M］.2版.济南：山东科学技术出版社，2006.