三角网格剖分方法及其在河道水流模拟中的应用

李小娟，孙建华

（江西省新干县黄泥埠水库管理局，江西 新干 331300）

0 引 言

随着数值模拟技术在工程中的广泛应用，人们对模拟计算精度的要求越来越高。网格的划分是直接影响数值计算精度的一个重要因素。多年来，许多学者致力于网格的研究，并取得了丰硕的成果。计算网格通常划分为结构网格和非结构网格。

结构网格包括代数方法中的多面法、无限插值法和通过求解等3种类型的微分方程生成的网格技术，结构网格具有编程快速、网格节点编号清晰等优点，但当计算区域为天然河道时，边界比较复杂，结构网格难以处理，生成网格的质量难以把握。

非结构网格自20世纪80年代以来得到了迅猛的发展，Delaunay三角形剖分方法[1]和前沿推进法（advancing front method）在工程中得到了广泛的应用。该方法对复杂边界有很强的适应性，能生成质量很高的三角形，但非结构网格点与点之间的编号十分杂乱，无规律可寻，难以在水沙二相流计算的离散格式中运用迎风性，不利于水流的模拟计算[2-3]。

本文充分发挥了结构网格和非结构网格的优点，提出一种新的网格生成方法。该方法采用使网格沿水流的方向由上游向下游逐步生成，在网格的自动生成过程中以前沿推进法的思想为主导，引入Delaunay三角形的概念，用以控制三角形的质量，最后生成优质的三角形网格。

1 河道边界的处理

本河道水流模拟研究中，取一进口断面和一出口断面，加上河道的天然边界，形成一封闭的区域，图1所示。

图1 河道边界离散示意图

图1中，AB为进口断面，CD为出口断面，BC和AD为河道的天然边界，要在ABCD区域中划分网格，首先要对ABCD的边界进行离散。分别给出A、B、C、D的坐标（XA，YA），（XB，YB），（XC，YC），（XD，YD），引入网格尺度[4]。网格尺度为某一段要求划分网格的尺寸。设A、B、C、D 的网格尺度分别为DA、DB、DC、DD，设定了网格尺度标志着边界离散的尺寸已经确定，边界的点数和坐标可计算出来。

2 区域内节点和单元的生成

区域内节点和单元的生成如下：

（1）将AB边作为进口边，AB上离散点为前沿点，由相邻前沿点所组成的边为前沿边，从前沿边向下游扩展。

（2）选定 AB边上的第一条离散边 A2，其中“2”为顶点名称，其边长为LA2，在有向线段中点向右边作垂直于的线段，线段长，H 点为扩展的一新点，其示意图如图2。

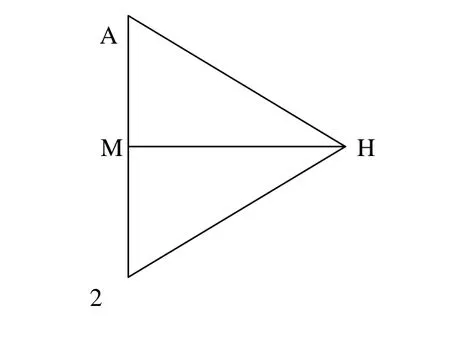
图2 前沿边扩展示意图

（3）判断点H是否为符合要求的扩展点。以H为圆心，以 αLAM为半径划圆（α 一般取 0.5～0.8），判断是否有离散点或前沿点被包括在圆内，若圆内没有前沿点，则（2）中所得的 H 点为所扩展的点，H 为新的前沿点，AH、H2为新的前沿边。如果圆周内有离散点，如图3。求出除H外的圆内各点对的望角，即∠AI2、∠AJ2、∠AK2、∠AL2、∠AM2，比较各望角的大小，显然∠AI2最大，于是选I为所扩展的新点，如果在 BC上，新增的前沿边为；如果在DA上，新增的前沿边为；如果点 I在上，新增的前沿边为和。至此边的扩展完成，重复步骤（1）～（3）对边进行扩展，直到最后一个前沿边扩展完毕。

（4）删除编号重合的三角形。在上述扩展过程中同一个前沿边有可能扩展了多次，也就是说对于同一个三角形可能重复计算了。比较各单元的节点编号，如果几个单元的节点编号完全相同则仅留下单元号最小的单元，其余的单元均删除。如45单元的节点编号分别为22、23、30；50 单元的节点编号分别为30、22、23。 两单元的编号完全相同，由于45＜50，故删掉50单元，只保留45单元，其余单元数大于50的单元其单元数均减1。如此类推，最终区域ABCD内没有重合的单元。

图3 确定最终扩展点示意图

3 网格的光滑处理

三角形网格优化的主要目的是使网格接近正三角形，保证网格的质量。网格的优化方法主要有“结构优化”和“位置优化”。前者调整网的拓扑结构，后者调整内部节点的位置。

3.1 网格的结构优化

在文献[5]中作者引入了节点的“度”的概念，定义度为共享该节点的单元数目。并得出三角形节点的度δ一般小于8，最佳取值范围为5≤δ≤8。因此，仅需要对δ等与3或4的三角形节点进行处理。

判断三角形节点的度，边界点除外，当δ＝3时，去掉该节点，其余三边拼成一新的三角形，如图4。去掉点D，ABC组成新的三角形。

图4 δ＝3 时转换图

当δ＝4时计算各单元中该角的角度，当角度大于100时需要添加边。如图5，假设∠AEB＞100；∠BEC＞100，在∠AEB和∠BEC间要添加一边，AB，BC分别为∠AEB和∠BEC对应的边，取出共享AB、BC边的三角形ΔAGB和ΔBFC，分别消去边AB和BC，连接EG和EF，使三角形得以优化。

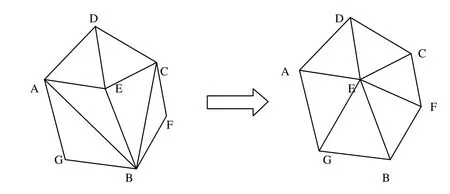
图5 δ＝4 时转换图

3.2 网格的位置优化

网格的位置优化通常用Laplacian均匀计算公式[6]：

XN、YN—分别为与I点连接的各点的横坐标和纵坐标。

上述公式是简单的线性平均，使I点处于所在面的几何中心。该计算公式在运用过程中变化很大，很有可能移到某个相邻的单元内，并且完全忽视了原来（XI，YI）对它的影响，为此对该种方法进行了改进，引入松弛迭代技术：

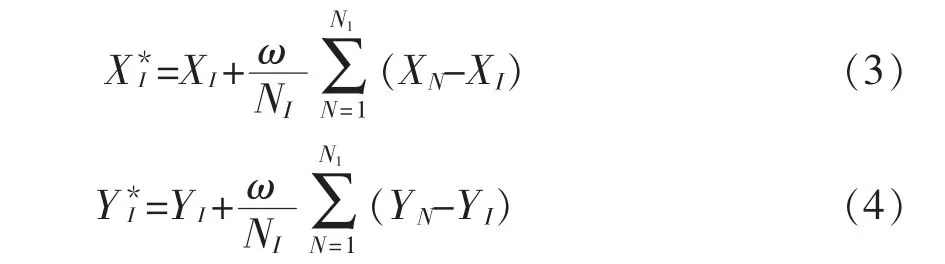
式中：（XI，YI）—原来 I点的坐标；

NI—与I点相连的点的个数，如图5中，与D点相连的点为A、B、C共有3个；

（XN，YN）—相连点的坐标；

ω—松弛因子，可以取1。

对于网格位置的优化可以进行多次光滑，每次光滑均取最新坐标，一般经过5～10次可以达到较好的效果。

4 三角网格剖分方法的应用

4.1 基本方程

水流连续方程：

式中：U、V—分别为垂线平均流速在x、y方向上的分量；

ZS、Zb—分别为水位和河底高程；

H—垂线水深；

ρ—水密度；

νt—紊流粘滞性系数；

τx、τy—分别为底部切应力在 x、y方向上的分量；

f—柯氏力系数，f＝2WsinΦ；（W 为地球自转角速度，Φ为地理纬度）。

其中，

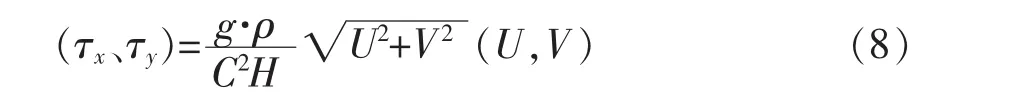
式中：C—谢才系数。

4.2 边界条件处理

对于不动边界条件，可分为以下4类处理：

（1）上游进口边界（开边界）Γ1，给出

（2）下游出口边界（开边界）Γ2，给出

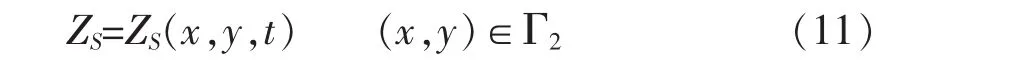
（3）不滑动岸壁边界（闭边界）Γ3，给出

（4）滑动岸壁边界（闭边界）Γ4，规定

4.3 计算实例

如图6为概化的平面河道，河道长2200 m，宽600 m，河道中存在一座小岛，河底比降设定为0.0001。采用本文提出的三角形网格自动生成方法，该区域共生成684个节点，1236个网格单元，网格长约50 m。当进口断面给定流量3000 m3/s，下游给定恒定水位3 m时进行计算。图7为根据生成的网格计算的流场图，可以看出水流从进口断面向下游流动，遇小岛后水流分流，在小岛后形成回流，且流速较小，该流速变化规律与实际情况相符。

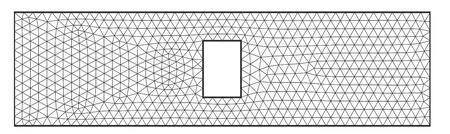
图6 河道网格划分

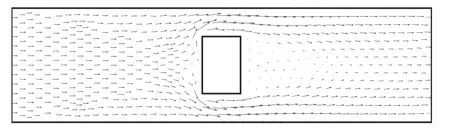
图7 河道平面流场图

5 结语

本文将波前推进法和Delaunay三角形剖分方法结合起来，选取进口断面为网格扩展的前沿，提出了适用于平面二维河道水流模拟的网格自动剖分方法，在平面河道中生成了优质的三角形网格。该方法能快速实现河道网格的自动剖分，生成后的网格具有优质、对边界的适应性强等特点，能提供数值模拟计算需要的前处理数据。基于生成的网格应用于水流模拟计算时，计算结果能充分反映水流变化的实际情况。

［1］杨晓东，刘春太，申长雨，等.内部带特征约束的任意平面域的三角形网格生成方法［J］.计算物理，2000（3）.

［2］张细兵.河道有限元网格自动剖分方法的研究［J］.长江科学院院报，2000（3）.

［3］吴 腾，钟德钰，张红武.水库自适应控制运用模型及其在亭口水库的应用［J］.水力发电学报，2010，29（3）：97－102.

［4］张 征，李孟国.三角形网格自动生成技术的应用［J］.水道港口，2001（3）.

［5］张均锋，刘桂斋，陈 刚.有限元平面元三角形网格的优化［J］.山东矿业学院学学报，1997（3）.

［6］罗特军，罗季军，汪 榴，等.有限元网格优化方法［J］，四川联合大学学报，1999（3）.