基于FDK反投影权重的锥束DSA重建算法

杨宏成，高 欣，张 涛1，

(1.中国科学院长春光学精密机械与物理研究所，吉林长春130000;2.中国科学院大学，北京100049;3.中国科学院苏州生物医学工程技术研究所，江苏苏州215163)

数字减影血管造影(digital subtraction angiography，DSA)是一种通过计算机把血管造影片上的骨与软组织的影像消除，仅在影像片上突出血管的X射线技术.近年来随着平板探测器(flat panel detectors，FPD)的引入，锥束DSA可获取血管3D影像信息.锥束DSA采用短扫描方式，可有效减少扫描时间、提高时间分辨率、降低射线剂量.但受扫描方式限制，锥束DSA很难获得类似CT的图像质量.针对短扫描方式的锥束重建算法，目前主要有两大类:一类是基于FDK的算法［1］，一类是基于Grangeat的算法［2］.与基于 Grangeat的算法相比，基于 FDK的算法重建速度快，空间分辨率高.但由于圆轨迹的短扫描方式不满足完全精确重建条件，基于FDK的短扫描重建算法存在锥束伪影.

目前改善锥束伪影的方法主要有以下两种:① 采用“圆弧 + 圆弧”［3］、“ 圆弧 + 线段”［4］、“圆弧+螺旋”［5］等扫描方式以满足完备重建条件，利用精确重建算法来进行图像重建;② 采用改进的FDK算法，很多学者提出了许多FDK类改进算法，如 CW-FDK［6］、CB-FBP［7］、ACE［8-9］等.这些改进方法的中心思想是通过一些操作来减少锥角增大时不精确重建形成的伪影，这些算法对锥角较小(小于±5°)情况有较高的重建质量.第1种方法要求增加轨迹精度高，增加了DSA机械设计难度;第2种方法当锥角大于5°时，改善效果有限.

文中拟提出一种针对DSA圆轨迹短扫描的FDK锥束重建算法.根据Radon空间数据缺失特点设计一种全新的反投影权重函数，将其引入圆轨迹短扫描锥束重建中.先分析锥束伪影形成的原因，提出一种反投影权重，并将其作为约束条件引入到Parker-FDK算法中实现抑制伪影的目的.采用无噪声投影数据、有噪声投影数据和自行研制的锥束DSA设备上采集的数据对新算法进行试验，列出该算法与Parker-FDK算法试验对比结果，并最终对算法的的性能给出总结.

1 算法及理论分析

1.1 FDK算法

FDK算法是 L.A.Feldkamp等人［10］把二维扇束重建公式推广到三维空间的锥束重建算法.图1表示锥束圆形扫描轨迹.

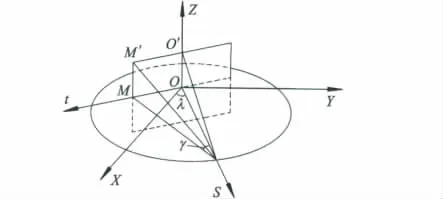
图1 圆轨迹短扫描锥束投影示意图

FDK重建公式可以表示为

式中:g(λ;u，v)为从平面探测器上获得的投影数据;λ为旋转角度;(u，v)为探测器系统下坐标值;γ为半锥角;D为射线源到探测器中心的垂直距离;h(u)为滤波函数;⊗表示一维卷积.

Liu Ying等［11］将 Parker窗函数引进到 FDK 算法中，提出了针对［0，π +2γmax］角度范围内圆轨道扫描的Parker-FDK重建算法.该方法利用类似FDK的方法进行重建.其中，γmax表示最大半扇角.重建过程包括加权、数据冗余补偿(Parker窗加权)、滤波和反投影，公式表示如下:

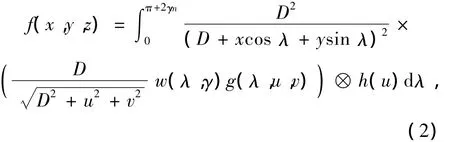
式中:w(λ，γ)为 Parker窗函数，表示为

图2为圆轨迹扫描Radon数据缺失示意图.

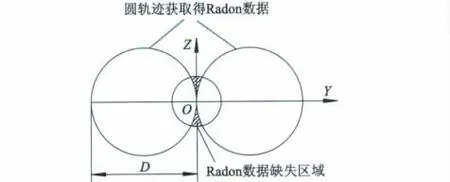
图2 圆轨迹扫描Radon数据缺失示意图

由图2可见，圆轨迹扫描方式只能采集到部分Radon数据，在旋转轴z轴方向上存在着较大的阴影区域，整个区域类似面包圈结构.而FDK类算法将这些阴影区域填充为0，这就是FDK类算法在大锥角区域产生锥束伪影的主要原因.故对阴影区域进行补偿是减少锥束伪影的一个思路.

1.2 反投影权重锥束重建算法

首先引入共轭射线和共轭射线权重.图3为共轭射线示意图.

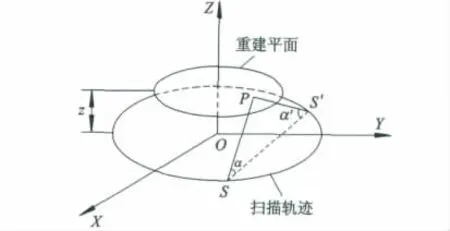
图3 共轭射线示意图

图3中，重建平面内任意一点P，扫描轨迹上的某一点S，两者之间的连线在扫描轨迹平面内的垂直投影的延长线与扫描轨迹的交点为S'，则S'P称为SP的共轭射线，S'则是S关于P点的共轭点.以α表示射线SP的锥角，α'表示共轭射线S'P的锥角，一般情况下，α≠α'.考虑共轭射线的连续性，对直接射线和其共轭射线采用不同因子进行加权处理，记作共轭射线权重.对于一组共轭射线来说，锥角小的那根射线投影的影响因子大一些.故可设共轭射线权重为

实际上，FDK算法是二维扇束重建公式在三维空间推广，并没有考虑离扫描轨道距离z不同的重建平面对反投影的影响.为此文中在FDK算法的反投影过程中引入基于距离权重的补偿因子，记作反投影权重(backprojection weight，bpw)，对 Radon 缺失数据进行补偿，从而改善锥束伪影.

综上所述，反投影权重应该是锥角α和距离z的函数，记作wbpw(α，z)，可表示为

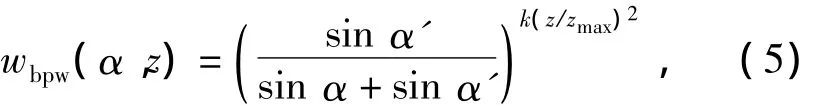
式中:k为(0，1)区间的松弛因子;zmax为轴向最大重建距离.x=-25 mm处的20°和200°时的反投影权重如图4所示.可以看出反投影权重随着|z|的增大而变大.

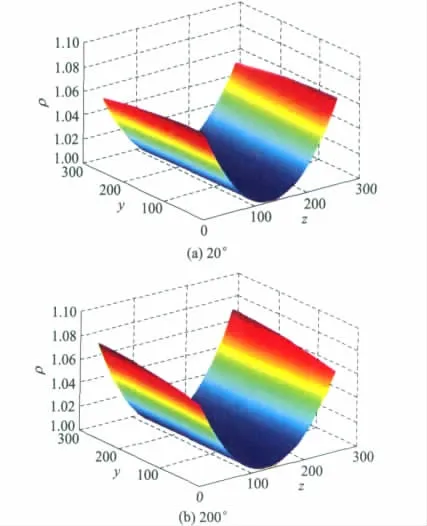
图4 x=-25 mm时20°和200°的反投影权重

由此文中提出了基于FDK的反投影权重锥束重建算法(back projection weighted FDK，BPWFDK).在公式2中引入反投影权重，反投影权重重建算法可表示为

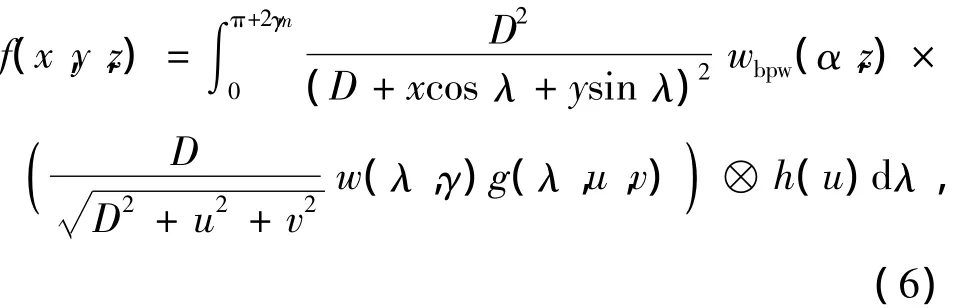
式中:h(u)为滤波函数;w(λ，γ)为Parker权重函数.应该注意的是:短扫描方式下，部分直接射线的共轭射线不在扫描轨迹上，如图5所示S'.这种情况，直接射线的反投影权重设置为1.

图5 短扫描方式下的共轭射线示意图

2 试验与结果

2.1 无噪声投影重建

文中基于三维Shepp-Logan头模型模拟投影数据，对Parker-FDK和BPW-FDK算法进行了比较.X射线源距离重建中心、探测器中心的垂直距离分别为400mm和600 mm，最大锥角和扇角都为18°，探测器阵列数为512×512，尺寸为0.39 mm×0.39 mm.图6给出了理论模型以及Parker-FDK和BPW-FDK算法的重建结果.切片图像大小为256×256，窗口显示范围为［1，1.05］.

图6 x=-25 mm时的无噪声重建结果切片图像比较

从图6可以看出:在投影锥角较大的区域，Parker-FDK算法重建图像出现了明显的锥束伪影;而BPW-FDK算法精确地重建出原物体.图7给出了图6重建的Sheep-Logan图像在x=-25 mm，y=0 mm和z=35 mm，x=0 mm处剖面灰度值比较.图7采用密度曲线的方法定量地显示上述重建结果，可以看出与Parker-FDK算法相比，BPW-FDK算法所获得的重建结果更好地拟合了模型的密度曲线.

图7 图6重建的Sheep-Logan图像的剖面灰度值比较图

表1给出了无噪声情况Shepp-Logan头模型之间的两个误差测度:归一化均方距离判据d、归一化平均绝对距离判据r作为重建质量好坏的两个标准.d，r定义如下:

式中:tu，v和ru，v分别为模型和重建后图像中第u行、v列的像素密度;¯t为模型密度的平均值.从表1可以看出，BPW-FDK算法归一化所获得结果的均方距离判据d和归一化平均绝对距离判据r均比Parker-FDK算法所获得的结果小，表明误差更小，重建图像质量更好.

表1 无噪声重建误差比较

2.2 有噪声投影重建

为了检测该算法的抗噪能力，在投影数据中加入0.1%的高斯随机噪声.图8是加入噪声后，用Parker-FDK和BPW-FDK算法重建的x=-25 mm的切片图像.仿真参数同无噪声投影情况下相同，切片图像窗口显示范围为［1，1.05］.重建结果表明当存在噪声时，BPW-FDK算法仍能够取得较好的结果.变化松弛因子k仍可以弥补当锥角较大时出现的锥束伪影问题.

图8 x=-25 mm时的有噪声重建结果切片图像比较

图9给出了图8重建的Sheep-Logan图像在x=-25 mm，y=0 mm和z=35 mm，x=0 mm处剖面灰度值比较.从图中可以看出当存在噪声时，与Parker-FDK算法相比，BPW-FDK算法所获得的重建结果仍更逼近模型的密度曲线.

图9 图8重建的Sheep-Logan图像的剖面灰度值比较图

表2给出了有噪声情况Shepp-Logan头模型之间的两个误差测度.从表2可以看出，BPW-FDK算法归一化均方距离判据d、归一化平均绝对距离判据r均比Parker-FDK算法所获得的结果小，表明重建图像质量更好，证明算法对有噪声数据的重建有效.

表2 有噪声重建误差比较

2.3 DSA数据重建

为了更好地验证BPW-FDK算法的性能，采用自行研制的DSA数据进行重建试验.DSA成像系统结构如下:X射线源距离重建中心、探测器中心的垂直距离分别为756.4 mm和1 060 mm，扫描角度为202°，最大锥角和扇角都为12°，探测器阵列数为768×1 024，探测器单元尺寸为0.388 mm×0.388 mm.分别使用 Parker-FDK、BPW-FDK算法对其重建.图10分别给出Parker-FDK和BPW-FDK算法重建的x=0mm处的切片图像，切片图像大小为256×256.重建物体为头骨模型，右下角为面颅，具有丰富的细节信息.可以看出，与Parker-FDK算法相比，BPW-FDK算法在右下角处通过对远离扫描平面进行补偿，可重建出更多细节，标明算法对实际DSA数据的重建是有效.

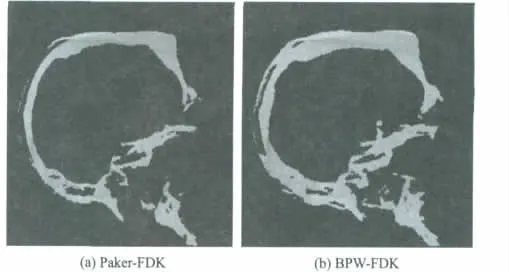
图10 DSA数据重建结果比较

BPW-FDK算法保持了滤波反投影结构，而滤波反投影算法中加权反投影运算量占总运算量的90%以上.BPW-FDK算法中反投影权重的引入并没有增加反投影复杂度，与Parker-FDK算法相比，计算效率并没有降低.

3 结论

文中分析了圆轨迹锥束扫描阴影区域形成的原因及对图像重建的影响，提出了基于FDK的反投影权重锥束重建算法，结论如下:

1)BPW-FDK算法保持了滤波反投影结构，反投影复杂度并没有增加，保持了Parker-FDK算法重建速度快的优点.

2)提出了基于距离权重的阴影区域补偿方法，设计了一种新型的权重函数，在反投影过程中将基于距离的反投影权重作用于滤波后的投影数据，重建出图像值.

3)仿真试验表明，与Parker-FDK算法相比，BPW-FDK算法重建图像的归一化均方距离判据和归一化平均绝对距离判据均降低了5%.

4)文中提出的BPW-FDK算法能够较好地重建出锥束短扫描下低对比度物体，减少锥束伪影，提高图像重建质量.

References)

［1］ Li Liang，Xing Yuxiang，Chen Zhiqiang，et al.A curve-filtered FDK(C-FDK)reconstruction algorithm for circular cone-beam CT ［J］.Journal of X-Ray Science and Technology，2011，19(3):355-371.

［2］ Zhu L，Starman J，Fahrig R.An efficient estimation method for reducing the axial intensity drop in circular cone-beam CT［J］.International Journal of Biomedical Imaging，2008，doi:10.1155/2008/242841.

［3］ Zambelli J，Nett B E，Leng S，et al.Novel C-arm based cone-beam CT using a source trajectory of two concentric arcs［C］∥Proceedings of SPIE.Bellingham:SPIE，doi:10.1117/12.713813 2007.

［4］ Zamyatin A A，Katsevich A，Chiang B S.Exact image reconstruction for a circle and line trajectory with a gantry tilt［J］.Physics in Medicine and Biology，2008，doi:10.1088/0031-9155/53/23/N02.

［5］ Schomberg H，van de Haar P，Baaten W.Cone-beam CT using a C-arm system as front end and a spherical spiral as source trajectory［C］∥Proceedings of SPIE.Bellingham:SPIE，doi:10.1117/12.811545.

［6］ 陈 炼，吴志芳，王钦娅.锥束 CT的分区短扫描FDK重建算法［J］.清华大学学报:自然科学版，2009，49(6):860-863.Chen Lian，Wu Zhifang，Wang Qinya.Segmentation short scan FDK reconstruction algorithm for cone-beam CT［J］.Journal of Tsinghua University:Science and Technology，2009，49(6):860-863.(in Chinese)

［7］ Tang X Y，Hsieh J，Hagiwara A，et al.A three-dimensional weighted cone beam filtered backprojection(CBFBP)algorithm for image reconstruction in volumetric CT under a circular source trajectory ［J］.Physics in Medicine and Biology，2005，doi:10.1088/0031-9155/50/16/016.

［8］ Zhu L，Yoon S，Fahrig R.A short-scan reconstruction for cone-beam CT using shift-invariant FBP and equal weighting［J］.Medical Physics，2007，34(11):4422-4438.

［9］ Nett B E，Zhuang T L，Leng S，et al.Arc based conebeam reconstruction algorithm using an equal weighting scheme［J］.Journal of X-Ray Science and Technology，2007，15(1):19-48.

［10］ Feldkamp L A，Davis L C，Kress JW.Practical conebeam algorithm［J］.Journal of the Optical Society of A-merica A，1984，1(6):612-619.

［11］ Liu Ying，Liu Hong，Wang Ying，et al.Half-scan cone-beam CT fluoroscopy with multiple X-ray sources［J］.Medical Physics，2001，28(7):1466-1471.