基于最大回正力矩的轮-地摩擦因数估计法

李 遥，张建武，管西强

(上海交通大学机械与动力工程学院，上海200240)

轮-地摩擦因数是对车辆控制系统尤其是车辆主动安全控制系统非常重要的一个量.它表征了汽车加速、刹车或者转向时地面所能提供的最大附着力.但是，在实际的行车过程中，轮-地摩擦因数却很难通过传感器直接测得.过去，针对轮-地摩擦因数的估计方法主要基于纵向动力学，并通过附着系数与滑移率的关系曲线求得［1-4］.但是，这种方法需要实时计算利用附着系数和车轮滑移率，且在非典型路面上很难保证计算精度.也有些学者提出可以基于侧向动力学来估计轮-地摩擦因数，但这些算法都要在侧向力接近极限时才能起作用，而这时车辆已接近危险工况，这使得估计算法很难有实际应用价值［5-6］.近年来，日本学者提出可以利用电动助力转向系统(EPS)自带传感器测量转向系回正力矩［7］，这使得基于侧向动力学估计轮-地摩擦因数的方法成为了可能［8-10］.笔者正是基于此，设计一种利用转向系最大回正力矩估计轮-地摩擦因数的方法，克服基于侧向力估计算法的缺点，具有很大的实际应用价值.

1 车辆模型

1.1 轮胎模型

Brush轮胎模型(BTM)［11］是轮胎侧偏角 α 和轮-地摩擦因数μ的函数.Brush轮胎模型的一般公式为

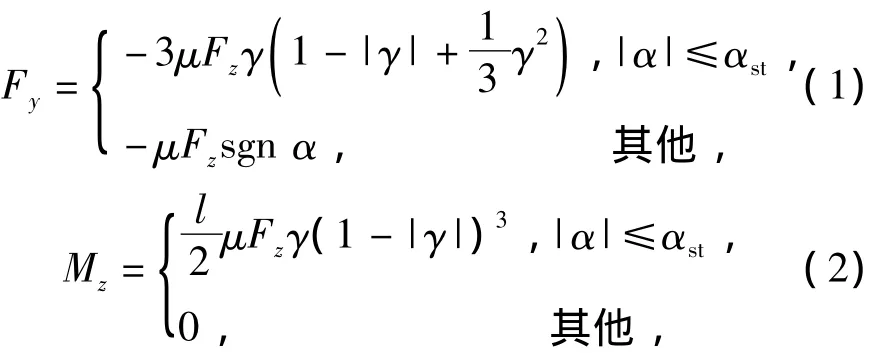
式中:Fy为轮胎侧向力;Mz为轮胎回正力矩;γ=θy×为轮胎侧偏刚度;l为轮胎接地长度;α为饱和侧偏角，α=arctan 1.

ststθy

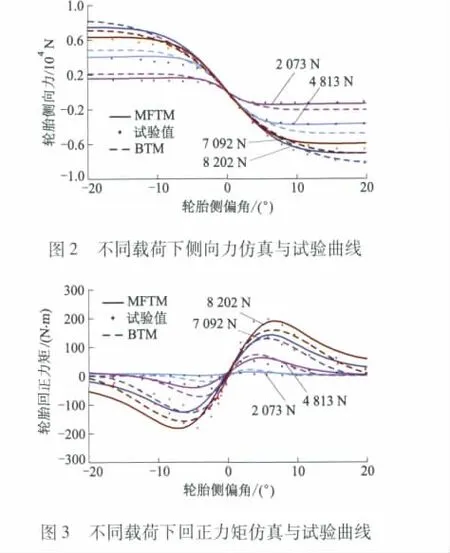
为了验证BTM的准确性，在台架(见图1)上做了一系列单轮试验并与公认比较准确的魔术轮胎模型［12］(MFTM)的值进行了对比.

图1 单轮台架

试验时，车轮速度大约为18 km·h-1，胎压为220 kPa.图2，3分别为不同载荷下的轮胎侧向力和回正力矩与轮胎侧偏角的关系.通过仿真结果和试验结果的对比可以发现，虽然魔术轮胎模型结果比Brush轮胎模型结果要更好一些，但Brush轮胎模型还是能比较准确地反映出车轮的侧偏特性的.比较相同载荷下的侧向力和回正力矩曲线可以发现，回正力矩要比侧向力更早地到达峰值.这说明，如果能充分利用回正力矩，则能比使用侧向力更早地估计出轮-地接触状况.

1.2 转向系统模型

Mz很难通过传感器直接测量得到，但是，当转向力矩可测时，整个转向系统总的回正力矩Ma［12］是可以被计算出来的，图4为前轮回正力矩示意图.

图4 前轮回正力矩示意图

由图4可以看出，由于主销后倾和轮胎变形，侧向力在前轮上的作用点要稍稍延后于主销连线在地面上的投影.这使得侧向力相对于主销轴的力臂被轮胎中心线分成了2个部分.轮胎回正力矩就是由侧向力作用在轮胎拖距上产生的力矩，而总的回正力矩则为侧向力在轮胎拖距ξp和主销后倾距ξc之和上产生的力矩.整个转向系统总的回正力矩则考虑了左轮和右轮综合作用的结果.

通过以上分析，Ma可表示为

式中:j为左轮或右轮.

因此，利用BTM求得轮胎侧向力和轮胎回正力矩就可以借助于式(3)计算出整个转向系统总的回正力矩Ma，从而进一步探讨Mamax与μ的关系.更重要的是，转向系统总的回正力矩也可以通过转向系的力矩平衡方程间接测得.忽略二阶导数项，则转向系总回正力矩为

式中:G1，G2为减速器和转向器速比;Td为扭矩传感器测量值;i，θ·分别为助力电动机电流和转速;cT为电动机力矩常数;c，cc分别为电动机和转向系当量阻尼系数.

所以，式(4)可通过EPS自带传感器测量得到而不需要添加任何额外传感器.另外，在实际测量中，为了减少测量噪声的干扰，使用了带遗忘因子的最小二乘算法进行滤波.

2 估计模型

通过以上的分析发现，轮胎回正力矩将先于侧向力达到最大值，且通过车载传感器能间接测得整个转向系的回正力矩.那么，如果最大回正力矩与轮-地摩擦因数存在某种简单的代数关系，则可以通过测得的最大回正力矩估计出轮-地摩擦因数的值.所以，有必要推导Mamax与μ间的代数关系.

2.1 最大回正力矩与轮-地摩擦因数的关系

转向系总的回正力矩Ma可以由式(3)计算得到.如果考虑整个前轴的情况，式(3)可以改写为

由于考虑整个前轴的载荷，故载荷的侧向偏移对计算没有影响，且忽略载荷的纵向再分配，并将式(1)，(2)代入式(5)可得

为了计算最大回正力矩Mamax，对上式求Ma相对于|γ|的偏导可得

由此可计算得，当Ma达到峰值时，

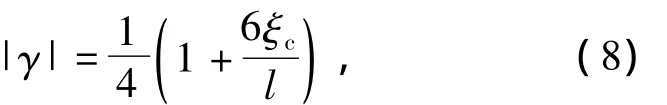
将式(8)代入式(6)可得

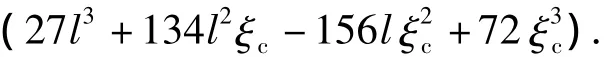
因此，

由式(10)可以清楚地看到，如果使用Brush轮胎模型，则轮-地摩擦因数μ与最大回正力矩Mamax存在简单的线性关系.并且，式(10)中的各项都是可以测得或简单计算得到的:轮胎接地长度l可以在充分考虑轮胎结构本身特点和弹性体之间接触的情况下用半解析的方法得到［13］，主销后倾距ξc跟转向结构的几何关系有关并且由结构间的运动学关系决定，前轴的垂向载荷仅计算静态时的载荷分配，转向系统总回正力矩的最大值Mamax可由式(4)计算得到.

2.2 最大回正力矩出现点的判断方法

最大回正力矩法最大的难点在于判断Ma何时达到了最大值.因为这种估计方法本身无法实时获得轮胎侧偏角，所以不能通过测量侧偏角满足式(8)来求得最大回正力矩出现的点.不过，如果逆向考虑，则当回正力矩处于最大值时，下式是满足的，即

首先假设在1个小范围内μ，Fzf和Cα1是常数，这样有考虑到轮胎侧偏角通常很小，故假设tanα≈α.因此，式(12)可以改写为

图5和曲线比较

事实上，在回正力矩达到峰值前，轮胎侧偏角还比较小，侧向力与侧偏角的关系曲线还处于线性区域，则

式中:β为车体质心侧偏角;ωr为车体质心横摆角速度;v为车体质心侧向速度;δ为前轮转角.

式(14)-(15)中各系数可写为如下形式:

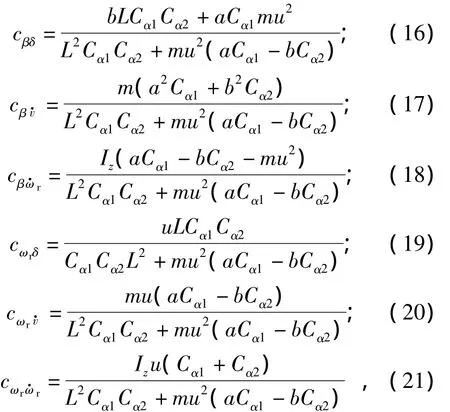
式中:m为整车质量;L为轴距;a为质心至前轴距离;b为质心至后轴距离;u为车速;Iz为绕z轴转动惯量.

如果设定MAMM算法只有在车速稳定后才会单独工作，则以上所有参数都可认为是常数.另外，由简单的运动学关系可得

忽略二阶导数项(¨v、¨ωr)，并对式(22)求导，可得

因此，第3个假设为

式中:kαδ为常数.

将式 (13)，(24)代入式(11)可得

需要特别提出的是，如果汽车安装有EPS或者其他可以测量转向力矩的先进转向系统，那么从推导过程可以看出，本算法不需要添加额外的传感器就可以估计出轮-地摩擦因数，具有巨大的价格潜力.

3 仿真和试验

为了验证估计方法的准确性，针对不同工况给出一系列仿真和试验结果.仿真和试验所用的车辆参数:质心至前轴距为1.423 m;质心至后轴距为1.117 m;质心高度为0.386 m;绕x轴转动惯量为284.5 kg·m2;绕z轴转动惯量为2 248.1 kg·m2;整车质量为1 535 kg;减速器速比为16.5;转向器速比为20;电动机力矩常数为0.02 N·m·A-1;电动机当量阻尼系数为0.003 34 N·m·s·rad-1;转向系当量阻尼系数为0.3 N·m·s·rad-1.

3.1 不同路面下的仿真计算

仿真中，前轮转角从20 s开始缓慢从0增加到0.3 rad，并使车速尽量保持在45 km·h-1左右.

为了使计算具有全面性，分别针对3种不同路面情况(μ =0.2，0.5，1.0)进行了仿真计算.前轴总的侧向力和回正力矩的时间历程曲线如图6所示.轮-地摩擦因数的估计结果如图7所示.为了使车速稳定，前20 s汽车保持直行，所以图6，7的计算结果均从20 s才开始记录.

从图7可以看出:在3种不同路面条件下，最大回正力矩法都可以较好地估计出轮-地摩擦因数的值，同时，在低附着路面上，不但回正力矩能更早地达到最大值，且轮-地摩擦因数的估计结果也要好于高附着路面.对比图6，7中μ=1.0的曲线可以发现，由于在估计模型中使用了回正力矩的信息，所以在侧向力到达极限前，估计模型已经能比较准确地估计出路面情况.

另外，通过仿真过程还发现，虽然之前已经介绍了找到最大回正力矩出现点的方法，但在实际计算过程中，如果计算步长太长，仍然有可能错过这个点而使估计结果出现较大偏差.但是，如果减小计算步长，则会牺牲计算速度从而使估计方法失去实际应用意义.所以在实际运用过程中，将进一步改进算法，使用最大回正力矩出现点周围的1个小范围来替代这个点，则式(25)变为

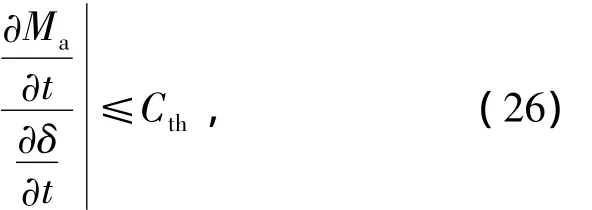
式中:Cth为常数.

3.2 蛇形试验

为了进一步验证估计算法，将蛇形试验的测量结果导入估计模型进行了计算.水泥路面试验场的摩擦因数为0.7～0.8，试验中车速保持在45 km·h-1左右.为了保持稳定，在测量开始后5 s汽车才开始转向.图8为测得的方向盘转矩.

图8 测得的方向盘转矩

图9为轮-地摩擦因数的估计结果.在最初转向的6.5～8.5 s的2 s时间内，由于式(26)的近似，所以在车轮转角不大时对摩擦因数有所低估.随着转角的增大，估计值迅速找到了实际值并保持稳定.在20 s之后，由于转角变小，摩擦因数再次被略微低估.

图9 轮-地摩擦因数的估计结果

图9说明:虽然最大回正力矩法忽略了纵向载荷的动态分配，但在纵向车速保持稳定的情况下，估计结果依然是具有相当的精度.考虑到最大回正力矩法具有的巨大价格潜力，这种估计方法在很多情况下都有比较大的实际应用价值.

4 结论

1)使用Brush轮胎模型后，可推导出转向系最大回正力矩与轮-地摩擦因数间存在线性关系.

2)在纵向车速保持稳定的情况下，可忽略载荷的纵向分配，则最大回正力矩法只需要借助EPS自带传感器就可以估计出轮-地摩擦因数而不需要任何额外的传感器.

3)最大回正力矩估计法在侧向力达到极限前就能估计出轮-地摩擦因数，可以更早地预测地面情况.

References)

［1］ 杨 财，李 亮，宋 健，等.基于轮胎力观测器的路面附着系数识别算法［J］.中国机械工程，2009，20(7):873-876.Yang Cai，Li Liang，Song Jian，et al.Road friction coefficient estimation algorithm based on tire force observer［J］.China Mechanical Engineering，2009，20(7):873-876.(in Chinese)

［2］ 刘 力，罗禹贡，李克强.基于归一化轮胎模型的路面附着系数观测［J］.清华大学学报:自然科学版，2009，49(5):723-727.Liu Li，Luo Yugong，Li Keqiang.Tire-road friction coefficient estimation based on normalized tiremodel［J］.J Tsinghua Univ:Sci＆Tech，2009，49(5):723-727.(in Chinese)

［3］ de Castro R，Aranjo R E，Cardoso JS，et al.A new linear parametrization for peak friction coefficient estimation in real time［C］∥Vehicle Power and Propulsion Conference.Piscataway，USA:IEEE，2010:1-6.

［4］ Kiencke U，Nielsen L.汽车控制:发动机，传动系统，以及汽车［M］.李道飞，俞小莉，译.2版.北京:高等教育出版社，2010:310-313.

［5］ Zong Changfu，Song Pan，Hu Dan.Estimation of vehicle states and tire-road friction using parallel extended Kalman filtering［J］.Journal of Zhejiang University:Science A:Applied Physics＆Engineering，2011，12(6):446-452.

［6］ Haffner L，Kozek M，Shi Jingxin，et al.Estimation of the maximum friction coefficient for a passenger vehicle using the instantaneous cornering stiffness［C］∥2008American Control Conference.Piscataway，USA:IEEE，2008:4591-4596.

［7］ Umeno T.Detection of tire lateral force based on a resolver mechanism ［J］.R＆D Review of Toyota CRDL，2005，40(4):14-19.

［8］ Ahn C，Peng H，Tseng H E.Estimation of road friction for enhanced active safety systems:algebraic approach［C］∥American Control Conference.Piscataway，USA:IEEE，2009:1104-1109.

［9］ Takagi F，Takeya A，Kurishige M，et al.An estimation method of the maximum tire-road friction coefficient using an electric power assist steering［C］∥AVEC10.UK:Loughborough University，2010:779-782.

［10］ Ahn C，Peng H，Tseng H E.Estimation of road friction for enhanced active safety systems:dynamic approach［C］∥American Control Conference.Piscataway，USA:IEEE，2009:1110-1115.

［11］ Abe M.Vehicle Handling Dynamics［M］.UK:Elsevier Ltd，2009:5-39.

［12］ Pacejka H.Tire and Vehicle Dynamics［M］.UK:Elsevier Ltd，2002:172-208.

［13］ 朱兴元，谢志民，阎相桥，等.轮胎接地长度和径向静刚度计算方法 ［J］.轮胎工业，1998，18(8):458-461.Zhu Xingyuan，Xie Zhimin，Yan Xiangqiao，et al.Determination for ground contact length and static radial stiffness of tire ［J］.Tire Industry，1998，18(8):458-461.(in Chinese)