无轴承异步电机最小二乘支持向量机逆解耦控制

杨泽斌，孙晓东，张新华，朱熀秋，刘贤兴

(1.江苏大学电气信息工程学院，江苏镇江212013;2.江苏大学汽车工程研究院，江苏镇江212013)

无轴承异步电机(bearingless induction motor，BIM)集旋转与悬浮功能于一体，不仅具有传统异步电机的所有特点，而且还具有磁悬浮轴承无接触、无磨损、无需润滑、无污染、寿命长等优点，在高速、超高速特种电气传动领域具有广阔的应用前景［1-2］.然而BIM具有十分复杂的电磁关系，其径向悬浮力、转速和磁链之间呈现出高度非线性和严重耦合性，大大降低了BIM系统在大范围内悬浮运行的稳定性及可靠性.为此，如何克服BIM系统内部非线性耦合对控制系统性能的影响，实现BIM多变量之间的高性能动态解耦控制，成为目前BIM研究的重点及难点.

文献［3］提出了一种近似线性化的控制策略来实现BIM径向悬浮力和电磁转矩之间的解耦控制，该方法计算量大，控制系统比较复杂;文献［4］采用矢量控制对BIM进行解耦控制，然而矢量控制只能实现径向悬浮力与转速之间的静态解耦，是一种稳态解耦控制方法;文献［5］采用微分几何方法实现了BIM二自由度径向位置的动态解耦控制，然而对于径向悬浮力与转速以及磁链之间的耦合特性，并没有给出有效的解决方法，并且微分几何方法需要转换到几何域中进行讨论，故数学工具比较复杂，不易掌握;文献［6］采用逆系统方法对BIM进行了解耦控制，克服了矢量控制只能实现静态解耦的不足，并且物理概念比较清晰直观，数学分析简洁明了，但是逆系统方法在实际应用中存在逆模型难以获得的瓶颈问题;文献［7］为了克服逆系统的不足，采用神经网络来辨识BIM的逆模型，解决了BIM逆模型难以求取的棘手问题，但是神经网络自身存在局部极点小、过学习、运算量大等缺陷，限制了神经网络逆方法的进一步应用.支持向量机(support vector machine，SVM)是在统计学习理论基础上发展起来的一种机器学习方法，很好地解决非线性、高维数、小样本、局部极小点等问题，具有较强的泛化能力［8］.由Suykens等提出的最小二乘支持向量机(least squares support vector machine，LSSVM)是一种扩展的SVM，它是SVM在二次损失函数下的一种形式，只求解线性方程组，计算速度快，近年来在非线性系统建模和控制中获得了很好的应用.［9］

文中拟以一台4极转矩绕组，2极悬浮绕组的BIM为研究对象，在介绍其径向悬浮力产生原理的基础上，进行可逆性分析，利用LSSVM建立BIM的逆模型，并将其与BIM原控制系统相串联，实现BIM径向悬浮力、转速和磁链之间的动态线性化解耦，在此基础上，针对每个解耦子系统设计线性闭环控制器，最后进行仿真研究，验证文中所提解耦策略的有效性.

1 BIM工作原理及数学模型

图1为BIM空载情况下径向悬浮力产生原理图.BIM定子槽中嵌放着极对数PB=1的悬浮绕组和极对数PM=2的转矩绕组(文中下标B，M分别表示悬浮绕组和转矩绕组参数，下同)，当2套绕组的极对数满足PB=PM±1时，2套绕组产生的磁场相互作用可以同时产生径向悬浮力和电磁转矩［10］.设悬浮绕组和转矩绕组每相串联的有效匝数分别为NB和NM.在2套绕组中分别通入电流IB和IM，则产生2极磁链ψB和4极磁链ψM.当2套绕组通以如图1所示方向的电流，此时在上侧气隙ψB和ψM的方向相同，则气隙磁通密度增强，而在下侧气隙ψB和ψM的方向相反，则气隙磁通密度减弱，从而产生沿y正方向的径向悬浮力Fy;如果在悬浮绕组NB中通入相反方向的电流，则可产生沿y反方向的径向悬浮力.同理，沿x方向的径向悬浮力可以通过在悬浮绕组NB中通入与IB垂直的电流获得.

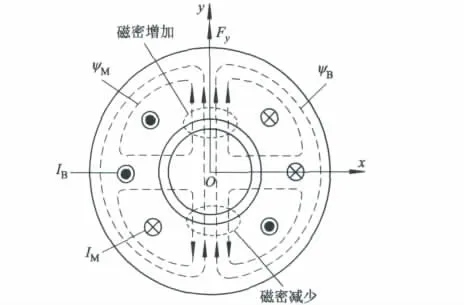
图1 BIM径向悬浮力原理图

BIM的电感矩阵L可以表示为

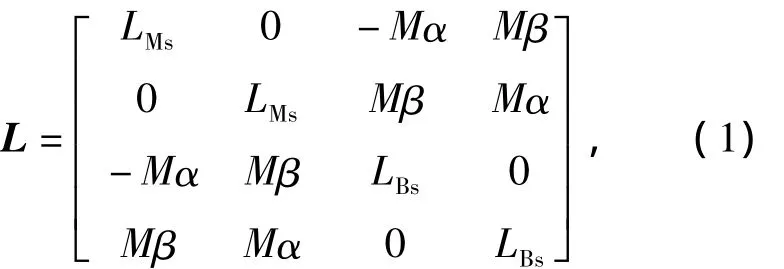
式中:α和β分别为转子在x和y方向的径向位移;LMs和LBs分别为转矩绕组和悬浮绕组的自感;M为2套绕组的互感系数，表示为

式中:μ0为空气磁导率;g0为气隙长度;R为转子半径;l为转子轴向长度.由能量转换关系可得BIM的磁场储能表达式为

式中:i= [iiii]T为BIM两套绕组定子

MdMqBdBq电流矩阵;iMd，iMq分别为转矩绕组电流在d，q轴上的分量;iBd，iBq分别为悬浮绕组电流在d，q轴上的分量.将变量代入式(3)可得磁能表达式为

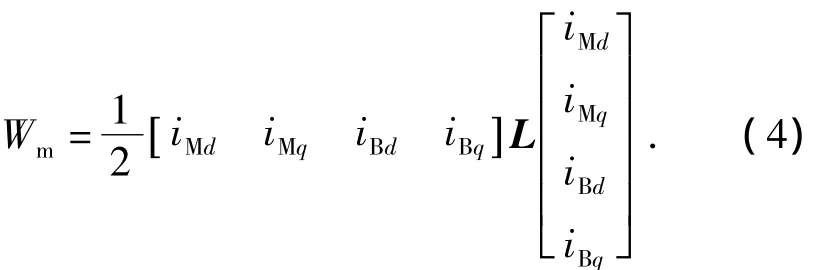
若忽略磁饱和，由虚位移原理，BIM径向悬浮力可表示为电磁储能对径向位移的偏导，因而BIM径向悬浮力Fx和Fy可以表示为

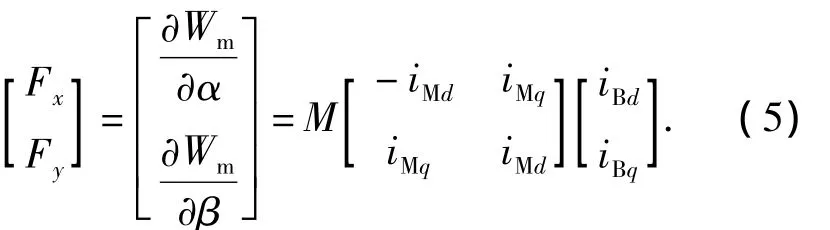
BIM中悬浮绕组与转矩绕组磁链相互作用，产生电机旋转与悬浮的电磁力.但是，与转矩绕组产生的磁场相比，悬浮绕组产生的磁场可以忽略不计，因此在忽略悬浮绕组产生磁场影响的前提下，BIM的转子磁链和电磁转矩满足如下方程:

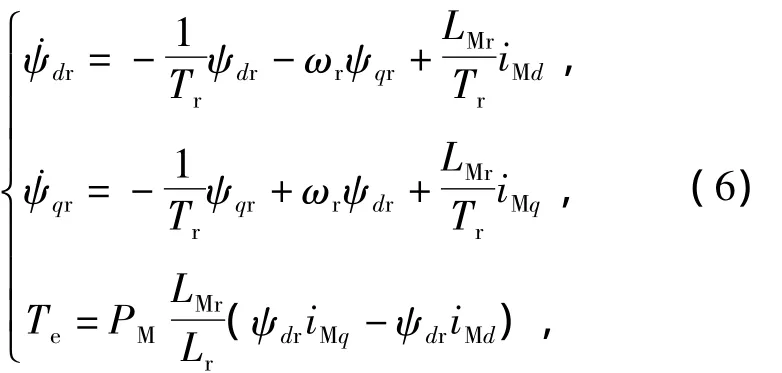
式中:ψdr，ψqr分别为 BIM 转子磁链在d，q轴上的分量;Te为电磁转矩;Tr为转子时间常数;ωr为转子角速度;LMr为转矩绕组与转子的互感;Lr为转子自感.

2 径向悬浮力模型

当BIM悬浮运行时，其转子的运动方程为

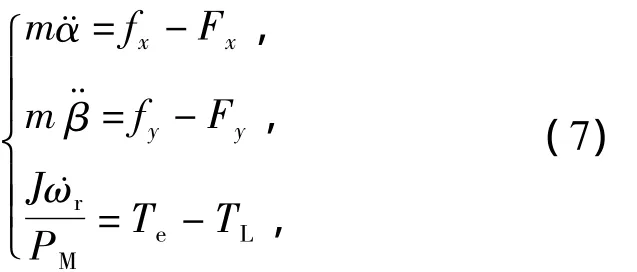
式中:m为转子质量;TL为负载转矩;J为转动惯量;fx=ksα，fy=ksβ分别为当转子偏离定子中心时的外界力;ks为位移刚度.

选取状态变量为

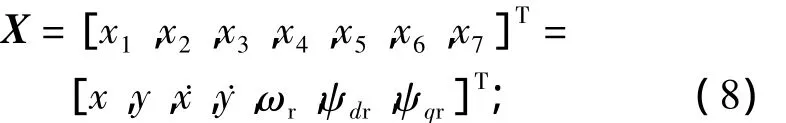
输入变量为

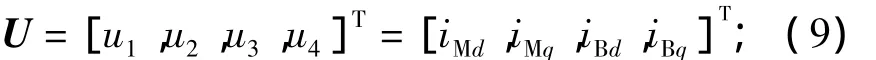
输出变量为

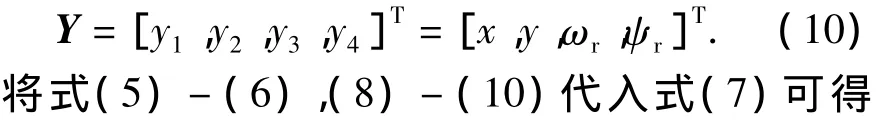
BIM的状态方程为

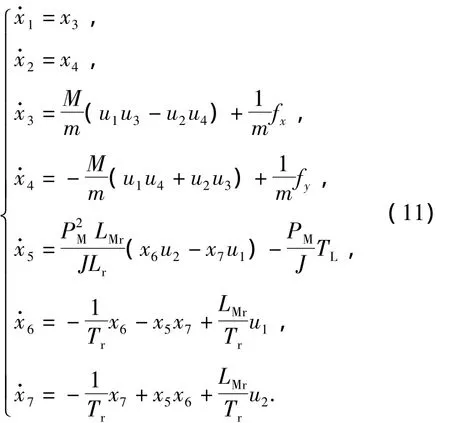
对BIM进行可逆性分析，首先对各输出变量求导直至方程中显含输入变量.由式(11)可得

由于Det(A)≠0，又因为BIM系统的相对阶数

4 α =(2，2，1，1)，且 ∑i=1αi=6＜7，所以BIM状态方程的逆系统存在.由隐函数定理可得，逆系统可表示为

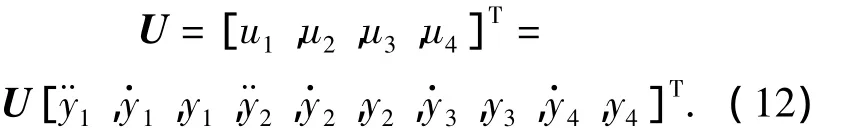
3 BIM的LSSVM逆解耦控制

3.1 LSSVM回归原理

LSSVM回归原理是选择函数y(x)=ωTφ(x)+b对未知函数进行估计，其中，xi∈Rm为权向量，b∈R为偏置值，非线性映射φ(x)将n组训练样本(xi，yi)(i=1，2，…，n)从原空间映射到高维特征空间.LSSVM的训练可通过求解如下优化问题来完成:

式中:γ为正则化参数;εi为不敏感损失函数的松弛因子.

引入拉格朗日乘子ai，求解式(13)的优化问题，得出

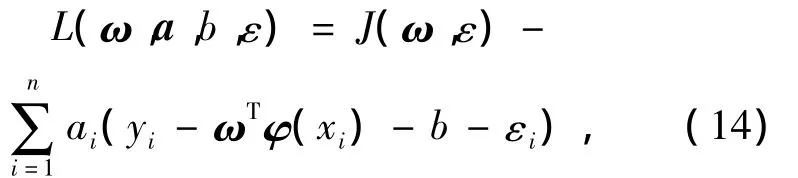
式中:ω =(ε1，ε2，…εn)T，a=(a1，a2，…an)T.根据Karush-Kuhn-Tucker条件，对拉格朗日函数 ω，a，b，ε分别求偏导，可将优化问题转化为以下线性方程组的求解问题

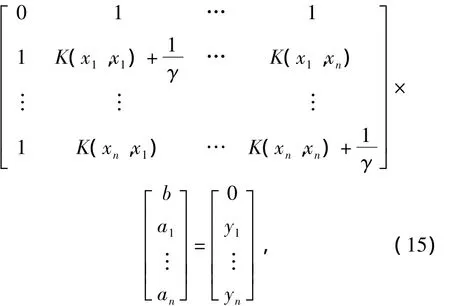
式中:K(xi，yj)为满足Mercer条件的核函数，核函数主要形式有径向基函数(RBF)、多项式Sigmoid函数等.鉴于RBF核函数的优点，文中选择RBF核函数为

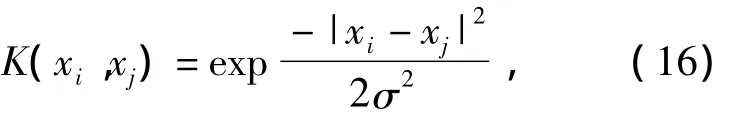
式中:σ为核宽度.利用式(15)求解a与b，再由式(14)求出ω，最后就可得出(xi，yi)的拟合方程为

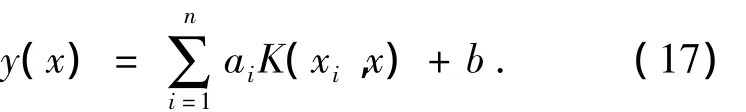
3.2 LSSVM逆解耦控制

采用LSSVM逆方法对BIM进行非线性动态解耦控制的步骤如下:

1)采样BIM的4路电流信号作为输入，二自由度径向位移、转速与磁链作为输出;然后采用高精度5点数值算法求取径向位移的一、二阶导数，转速和磁链的一阶导数，从而构成训练样本集和.由于在实际应用中，采样获得的数据不在一个数量级，为此将数据进行规范化处理.

2)LSSVM辨识的模型在很大程度上取决于正则化参数γ和核宽度σ的选取，因此为了提高BIM逆模型的建模精度和鲁棒性，采用自适应遗传算法对参数γ和σ进行优化，最后得到优化后的参数为:γ =1 800，σ =1.9.

3)采用LSSVM加积分器s-1来构造BIM的LSSVM逆，并将LSSVM逆置于BIM之前，LSSVM逆与BIM构成伪线性系统，其等效成4个解耦的积分型线性子系统，分别为2个位置二阶积分型伪线性子系统、1个速度一阶积分型和1个磁链一阶积分型伪线性子系统，其结构如图2所示.

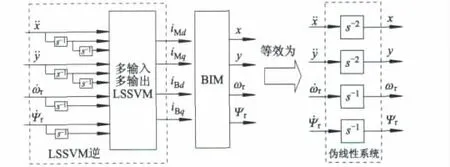
图2 BIM的伪线性系统

4)针对线性化解耦得到的4个积分子系统，采用PID调节器设计方法分别设计2个位置控制器、1个速度控制器和1个磁链控制器，并由此构成线性闭环控制器;最后将线性闭环控制器和LSSVM逆一起构成LSSVM逆控制器来实现BIM径向悬浮力、转速和磁链的独立控制，从而实现BIM转子稳定悬浮运行.图3是BIM的LSSVM逆解耦控制结构框图.

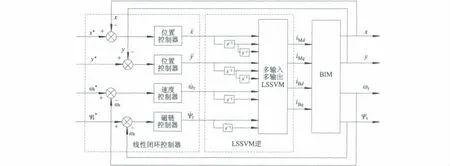
图3 BIM的LSSVM逆解耦控制结构框图

4 仿真与分析

以试验样机为对象，样机参数如下:转矩绕组、悬浮绕组极对数分别为2和1，转子质量为2.85 kg，转动惯量为0.007 69 kg·m2，转子电阻为11.48Ω，转子时间常数为1.46×10-2s，转子电感为0.167 78 H，定转子互感为0.158 56 H，2套绕组互感系数为78.2 H·m-1.

在仿真试验研究中，为了验证文中所提BIM的LSSVM逆解耦控制策略的有效性，对比研究了逆系统方法解耦控制.图4和图5分别为采用逆系统方法和LSSVM逆方法的解耦控制结果图.

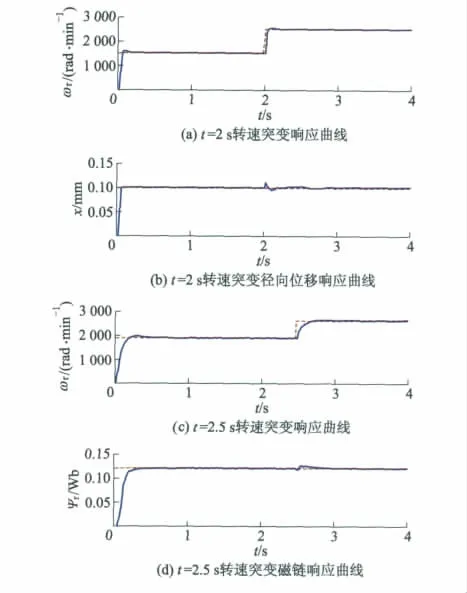
图4 逆系统解耦控制结果

图4a，4b为采用逆系统方法时转速与x方向径向位移之间的解耦结果图，在t=2 s时，转速由1 500 rad·min-1突变到 2 500 rad·min-1，此时x方向径向位移产生了明显抖动;图4c，4d为采用逆系统方法时转速与磁链之间的解耦结果图，在t=2.5 s时，转速由2 000 rad·min-1突变到2 500 rad·min-1，此时转速的突变对磁链产生了明显的影响.由图4可知，逆系统方法并未实现BIM径向位移、转速与磁链之间的动态解耦.

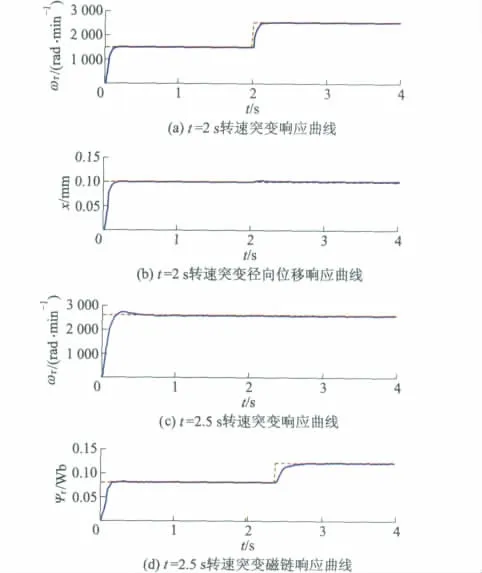
图5 LSSVM解耦控制结果

图5a，5b为采用LSSVM逆方法时转速与x方向径向位移之间的解耦结果图，在t=2 s时，转速由1 500 rad·min-1突变到 2 500 rad·min-1，此时转速的突变并未对x方向径向位移产生影响;图5c，5d为采用LSSVM逆方法时转速与磁链之间的解耦结果图，在t=2.5 s时，磁链由0.75 Wb突变到0.95 Wb，此时磁链的突变未对转速产生影响.由图5可知，LSSVM逆方法实现了BIM径向位移、转速与磁链之间的动态解耦，而且采用LSSVM逆方法比采用逆系统方法系统的稳定性能更加优良.

5 结论

文中针对BIM这一非线性、强耦合的多输入输出系统，提出了一种基于LSSVM逆的动态解耦控制策略，得到以下结论:

1)BIM是一个4输入4输出的6阶非线性、强耦合复杂系统，而且BIM系统是可逆的.

2)LSSVM逆方法结合了LSSVM的非线性回归能力与逆系统方法线性化解耦的优点，可以在不依赖BIM精确数学模型的前提下，通过对样本的非线性回归，得到BIM系统理想的逆模型.

3)LSSVM逆解耦控制方法，可以将BIM系统解耦为伪线性系统，并且通过设计伪线性系统的闭环控制器，使BIM系统获得优良的动、静态特性，真正实现径向位移、转速与磁链之间的非线性动态解耦.

References)

［1］ 朱熀秋，王成波，张伟霞.基于电感矩阵的无轴承电机径向悬浮力模型［J］.江苏大学学报:自然科学版，2009，30(1):53-57.Zhu Huangqiu，Wang Chengbo，Zhang Weixia.Mathematic model of radial suspension force for bearingless motors based on inductance matrixes［J］.Journal of Jiangsu University:Natural Science Edition，2009，30(1):53-57.(in Chinese)

［2］ Hiromi T，Katou T，Chiba A，et al.A novel magnetic suspension-force compensation in bearingless induction motor drive with squirrel-cage rotor［J］.IEEE Transactions on Industry Applications，2007，43(1):66-76.

［3］ Schoeb R，Bichsel J.Vector control of the bearingless motor［C］∥Proceedings of the fourth International Symposium on Magnetic Bearings.Zürich:［s.n.］，1994:327-332.

［4］ 朱熀秋，沈玉祥，张腾超，等.无轴承异步电机数学模型与解耦控制［J］.电机与控制学报，2007，11(4):321-325.Zhu Huangqiu，Shen Yuxiang，Zhang Tengchao，et al.Mathematics model and decoupling control for self-bearing induction motors［J］.Electric Machines and Control，2007，11(4):321-325.(in Chinese)

［5］ Dong Lei，Liu Xianxing，Sun Yuxin.Decoupling control of the bearingless induction motor based on differential geometry variable-structure method［C］∥Proceedings of the26th Chinese Control Conference.Piscata way:IEEE Computer Society，2007:17-21.

［6］ Zhu Huangqiu，Zhou Yang，Li Tianbo，et a1.Decoupling control of 5 degrees of freedom bearingless induction motors using α-th order inverse system method［J］.Acta Automatica Sinica，2007，33(3):273-278.

［7］ 孙晓东，朱熀秋.基于神经网络逆系统理论无轴承异步电动机解耦控制［J］.电工技术学报，2010，25(1):43-49.Sun Xiaodong，Zhu Huangqiu.Decoupling control of bearingless induction motors based on neural network inverse system method［J］.Transactions of China Electrotechnical Society，2010，25(1):43-49.(in Chinese)

［8］ Vapnik V N.An overview of statistical learning theory［J］.IEEE Transactions on Neural Net wroks，1999，10(5):988-999.

［9］ 程启明，杜许峰，郭瑞青.基于最小二乘支持向量机的多变量逆系统控制方法及应用［J］.中国电机工程学报，2008，28(35):96-101.Cheng Qiming，Du Xufeng，Guo Ruiqing.Decoupling compound control method based on least squares support vector machines multivariable inverse system and its application［J］.Proceedings of the CSEE，2008，28(35):96-101.(in Chinese)

［10］ 朱熀秋，成秋良.基于磁链等效虚拟绕组电流分析方法的无轴承电机径向悬浮力控制［J］.科学通报，2009，54(2):262-268.Zhu Huangqiu，Cheng Qiuliang.bearingless motor's radial suspension force control based on flux equivalent with virtual winding current analysis method［J］.Chinese Science Bulletin，2009，54(2):262-268.(in Chinese)