基于GPU的高速FHT计算及性能分析

张大兴，刘雁健，韩 锋，章建芬

(杭州电子科技大学图形图像研究所，浙江杭州310018)

0 引言

快速哈特利变换(Fast Hartley Transform，FHT)是一种常见的将数据从时域转换到频域的变换算法。与FFT、DCT、DWT等变换算法相比，FHT具有计算简便，运算量少，效率高及存贮需求低等优势，因此，在信号处理及图像处理等领域FHT有着广泛的应用［1－2］。然而，当面对海量数据时，传统的FHT算法处理速度依然难以满足实时性较高的系统需求。近年来，微电子产业的发展使得图形处理器(Graphic Processing Unit，GPU)的性能得到极大提高，GPU硬件结构采用更多的晶体管用于数据处理，而非数据缓存和流控制，适于解决那些高密度重复性高的计算问题。目前，利用GPU进行通用计算已在众多工程领域得到广泛的应用［3］。因此，本文通过深入分析FHT算法的并行特性，提出一种高速的并行FHT算法，并根据CUDA存储架构特点，实现了对FHT算法的加速及优化。

1 CUDA架构及编程模型

计算统一设备架构(Compute Unified Device Architecture，CUDA)是NVIDIA公司提出的一种通用并行计算平台和编程模型。CUDA中将CPU作为主机，GPU作为设备，以CPU来控制程序整体的串行逻辑和任务调度，而让GPU来运行一些能够被高度线程化的数据并行部分，即GPU与CPU协同工作。在CUDA程序中，一个kernel函数并行线程数量在主机端启动时确定，所有线程以网格的方式组织，一个网格包含多个块，不同块之间不需要同步，而一个块内又包含多个线程，同一块内线程不仅能够并行执行，还能通过共享存储器和栅栏通信，设置syncthread()”内部指令可以实现块内线程同步。这样，同一网格内的不同块之间存在不需要通信的粗粒度并行，而一个块内的线程之间又形成了允许通信的细粒度并行，这就是CUDA的双层线程模型。

2 基于CUDA的FHT算法

2.1 FHT算法

假设一个序列F有N个元素，F(i)表示其第i个元素，一维DHT正逆变换定义如下:

式中，casθ=cosθ+sinθ。如果直接按DFT定义运算，其时间复杂度为O(N2)，而采用快速算法(FHT)，则时间复杂度可降低至O(Nlog2N)［4］。FHT的主要思想是对于规模为N=2p的数据，首先按奇偶位序调整，然后进行p次蝶形运算，每一次蝶形运算的输出是下一次蝶形运算输入，最后得到正序的FHT结果。假设第r次蝶形运算结果为Hr，其计算公式如下:

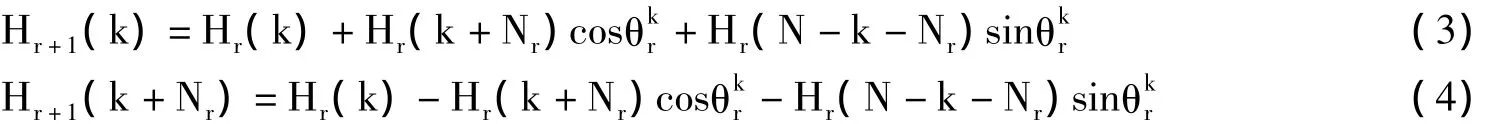
2.2 FHT并行特征分析

FHT算法计算过程包含p次蝶形运算，每一次蝶形运算数据输入是上一次蝶形运算输出，因此后一次蝶形运算必须等待上一次蝶形运算完成后才能开始，即p次蝶形运算只能串行执行。根据式3、4不难发现，FHT算法每一次的蝶形运算内部均包含了N次运算，如果将式3、4称为一组运算，则每一次蝶形运算过程可以看做是N/2次组运算过程，组和组之间数据没有相关性，如果用一个线程完成一组运算，则可通过N/2个线程并行完成一次蝶形全部运算。运算时需要计算的值，根据定义对其转换如下:由式5可知t的取值最小0，最大是N－1，因此可以采用查表法计算正弦因子和余弦因子的值。

2.3CUDA程序实现FHT

根据Nvidia公司发布的CUDA编程指南说明，要想获得较高的性能，程序必须最大程度的并行化，并尽可能的优化数据的存储组织。

对于规模为N=2p的数据，采用N/2个线程并行执行，每个线程生命周期是从第1级蝶形运算开始至第p级的蝶形运算结束，一个线程在一次蝶形运算中只负责一组数据的运算，完成后同步，等待同级的所有线程均完成计算后共同进入下一级蝶形运算。线程根据自身的id号选择组数据。并行FHT算法实现流程如图1所示。

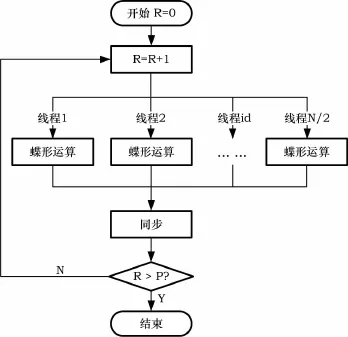
图1 FHT算法CUDA实现流程图

CUDA存储模型中，提供了多种不同的地址空间。寄存器和共享存储器位于GPU片内，属于高速存储器，访存一般只需一两个时钟周期。寄存器为每个线程私有，且空间有限。共享存储器可以被同一块中的所有线程共同访问，且地址空间较大。GPU片外存储器包括纹理存储器、常量存储器、局部存储器和全局存储器。在访存速度上，片外存储器远慢于片内存储器，由于纹理存储器和常量存储器提供了片内缓存加速对片外显存访问，因此两者的访存速度比局部存储器和全局存储器要快的多。基于上述分析，对存储组织的优化有以下3点:(1)kernel程序中，在计算开始前先将相关的数据从全局存储器中拷贝至共享存储器，计算结束后再写回全局存储器。这样中间的计算过程将只与共享存储器交互，大大降低访存延时;(2)纹理存储器存储正弦和余弦因子。纹理存储器是只读的且提供了片内缓存加速，因此非常适合查表类操作。具体做法是，首先定义两个一维的长度均为N的纹理存储空间，然后计算好所有的正弦和余弦因子值并依次存入该纹理存储器中，最后，程序在运行时根据索引值t以纹理摄取的方式获得对应正弦和余弦因子值;(3)存储器中的数据按能够合并访问的要求进行字节对齐，合并访问能够明显的提高程序的性能。由于NVIDIA GPU硬件设计上将共享存储器被组织成16个bank，当多个线程同时访问属于同一bank的数据，可能会产生bank冲突，冲突将导致数据串行访问，降低访存效率。因此，共享存储器上的数据应按16的倍数组织，避免发生bank冲突。

CUDA程序中需要两次拷贝操作(数据导入和导出)。为了降低数据拷贝延时，每次应拷贝尽可能多的数据，减少拷贝次数。此外，CUDA还提供了一种分页锁定主机内存技术［5］，该技术允许一部分主存空间映射到设备中，相当于设备可以直接读写主存，避免了在主存和显存之间的来回拷贝操作，但这是以牺牲主机端的性能为代价的，因为主机端被禁止访问映射到设备上的主机内存空间。

FHT算法CUDA实现的kernel代码如下:

3 实验结果及分析

为了验证本文提出算法的实际性能，分别在GPU上实现了基于CUDA的FHT算法和CPU上传统的FHT算法。实验硬件配置:(1)CPU双核Inteli5－2400，主存3.24 G;(2)GPU 采用 Nvidia GTS 450，显存512 M。实验程序分别在VS2008和CUDA5.0环境编译运行。实验使用图像数据作为输入，首先对图像按8×8分块，然后对每一块做FHT变换。Nvidia GTS 450允许一个block中最多有1 024个线程，每个block最大使用的共享存储空间是48 kB，如果数据规模很大则需要分多次导入。本实验测试时设置每个block 512个线程，每次最多导入32×220个数据。表1列出了不同大小的图像输入FHT算法在CPU和GPU上运行时间，其中GPU这一列指FHT算法在GPU中的纯计算时间，GPU v1和GPU v2的时间包含了计算时间和主机和设备之间数据拷贝时间，其中GPU v2采用CUDA分页锁定主机内存技术，而GPU v1未采用。

表1 FHT算法在CPU和GPU上运行时间对比(ms)

图2 GPU与CPU FHT算法运行时间的加速比

表1的实验结果显示:(1)并行的FHT算法比其传统算法有较大优势，且随着数据规模的增长，优势表现的越明显;(2)按常规的GPU编程方式，当数据规模较小时，主机和设备之间数据来回拷贝开销可能会抵消掉并行计算带来的优势，甚至会比CPU还慢;(3)采用CUDA分页锁定主机内存技术可以大大的减少主机和设备之间数据拷贝开销;(4)随着数据规模的增大，GPU相对于CPU的运算速度的并不是线性的增长。FHT算法CPU与GPU运行时间的比值如图2所示。可以看出，随着数据规模的增大，其比值增长逐渐趋于缓和，这是因为GPU内部处理器的个数是一定的，如本文实验用的GPU有192个处理器，当数据规模超过GPU每次最大并行量时，后一批数据不得不等待前一批数据处理完后才开始处理，导致GPU相对于CPU的运算速度提高倍数减缓。

4 结束语

本文针对传统的FHT算法不能满足海量数据实时处理的需求，提出并实现了基于CUDA的高速并行FHT算法，根据FHT算法分治特性，将数据映射到多线程并行执行，同时充分利用CUDA中共享存储器和纹理存储器的高速访存能力，优化了算法的存储组织。实验结果分析表明了该算法的高效性。目前，本文的算法只在CUDA平台中实现，下一步的研究目标是将算法应用到不同的平台，并与实际应用结合起来。

［1］维基百科.离散哈特利转换［EB/OL］.http://zh.wikipedia.org/wiki/离散哈特利转换，2013－03－13.

［2］Castleman K R.数字图像处理:英文版［M］.北京:电子工业出版社，2008:237－240.

［3］吴恩华.图形处理器用于通用计算的技术、现状及其挑战［J］.软件学报，2004，15(10):1 493－1 504.

［4］Bracewell R N.The fast Hartley transform［J］.proceedings of the IEEE.1984，72(8):1 010 －1 018.

［5］Nvidia.CUDA C Programming Guide［EB/OL］.http://docs.nvidia.com，2013 －07 －19.