基于粒子群优化的非平滑非负矩阵分解算法

戴华平，王 旭，胡红亮，王玉涛

(浙江大学工业控制研究所，杭州 310027)

1 概述

随着成像光谱技术的不断发展，通过成像光谱仪采集得到的遥感图像包含了越来越丰富的空间、辐射和光谱信息。影响光谱技术进一步发展的关键问题是高光谱图像中混合像元的广泛存在，混合像元限制了遥感应用的精度，降低了物质分类的准确性。因此，有效分解混合像元对于高光谱技术的发展具有重要意义[1]。

非负矩阵分解(Nonnegative Matrix Factorization,NMF)[2]是一种新的矩阵分解方法，目前已经被用于高光谱的混合像元分解。然而非负矩阵分解只是提供了非负性约束，这远不能很好地解决混合像元的分解问题。对于高光谱数据来说，除了非负性约束之外，稀疏性也是一个重要的约束条件，即任何端元的丰度分布一般都不会充满整个图像空间。文献[3]提出的非平滑非负矩阵分解(nonsmooth Nonnegative Matrix Factorization, nsNMF)算法被用于高光谱图像分解并显示出良好的效果，但是NMF和nsMNF具有的共同缺陷是容易陷入局部最小值，限制了高光谱解混的精度。

粒子群优化(Particle Swarm Optimization, PSO)[4]算法又称微粒群算法，是由Kennedy J和Eberhart R C等人于 1995年开发的一种演化计算技术，来源于对一个简化社会模型的模拟。粒子群算法可以解决多数的优化问题，并且它具有简单、高效和鲁棒性强的优点。

本文提出了一种基于PSO的nsNMF新算法，将nsNMF得到的结果作为PSO的初始值，每次迭代过后重新采用nsNMF进行更新，直到找到全局最优值。

2 线性光谱混合模型

线性光谱混合模型(Liner Spectral Mixture Model,LSMM)[5]在高光谱图像分析中有着广泛的应用。在线性光谱混合模型中，像素的观察值等于各端元的光谱特征按照它们的丰度进行线性组合，数学模型表述如下：

其中，矩阵 R ∈RL×N表示L个波段的遥感图像，每个波段有N个像素。 M =[m1, m2,… ,mp]∈ RL×P，称为端元光谱矩阵，mj对应着第 j个端元的光谱特征，P表示端元个数。 S =[s1, s2,… ,sp]T∈RP×N为丰度矩阵， sj=[sj1,sj2,… ,sjN]T ∈RN×1表示某一个端元上的所有像素的丰度。根据丰度的物理意义，丰度必须满足和为一约束和非负约束：

3 非平滑约束的非负矩阵分解

对于高光谱数据来说，除了非负性约束和全加性约束之外，稀疏性也是一个重要的约束条件。一般情况下，任何端元的分布都不会充满整个高光谱图像的空间。混合像元中包含的只是几种端元，而不是所有的端元。每个端元只是分布在高光谱图像空间中的某些区域，具有一定的稀疏度。对于线性混合光谱模型(LSMM)来说，一个矩阵的稀疏性必然导致另一个矩阵的非稀疏性(平滑的)，使得最终的乘积可以更好的拟合观测信号，这一点恰好加强了光谱信号的平滑性特征[3]。

给定一个L×N非负矩阵R，其中Rij≥0，非负矩阵分解算法找到2个非负矩阵M ∈RL×P和S ∈RP×N，所以得到：

为寻找一个近似的分解过程，使得R≈MS，通常定义R和MS的欧氏距离作为目标函数来保证逼近效果，即：

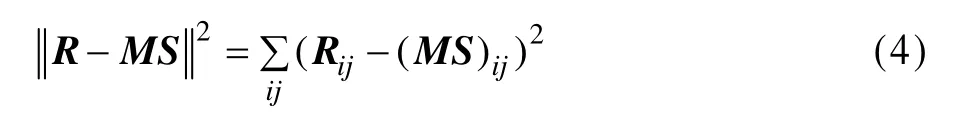
当且仅当R=MS时，上式取到最小值0。其中，Mij≥0,Sij≥0,∀ i, j 。

应用 nsNMF去分解混合像元，为达到全局稀疏性[3]，Montano 等人引入一个“平滑”矩阵C∈RP×P[4]到混合模型式(4)中：

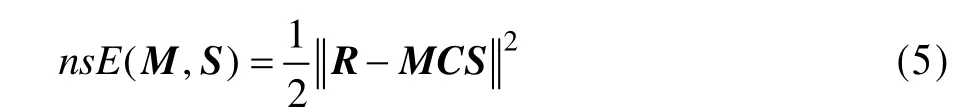
其中，C是一个正对称阵，其定义为：

其中，Ip是P×P维的单位矩阵；1p是元素全部为1的P×1维向量；稀疏因子θ满足0 ≤ θ≤ 1。矩阵M的非稀疏性使得矩阵S为稀疏矩阵，同时矩阵S的非稀疏性也使得矩阵M为稀疏矩阵。在光谱解混问题中，只需要端元分布矩阵S稀疏的，因此，更新规则如下：

其中，α和β为规则化系数。

当且仅当M和S达到稳定点时，目标函数式(5)不在变换。此外为了满足端元分布的全加性约束，在每一步迭代之后还要对丰度矩阵进行归一化运算：

4 非平滑非负矩阵分解的粒子群优化

4.1 粒子群优化算法

粒子群优化算法首先初始化一群随机粒子，然后通过迭代找到该种群的最优解。在每一次迭代中，每个粒子通过跟踪2个极值来更新自己。一个是粒子本身的最优解，称个体极值Pbest，另一个是整个种群的最优解，称全局极值Gbest，在本文中Gbest是一个矩阵且每个元素值相等。

种群中每个粒子在找到上述2个极值以后，根据以下公式来更新速度和位置[6]：

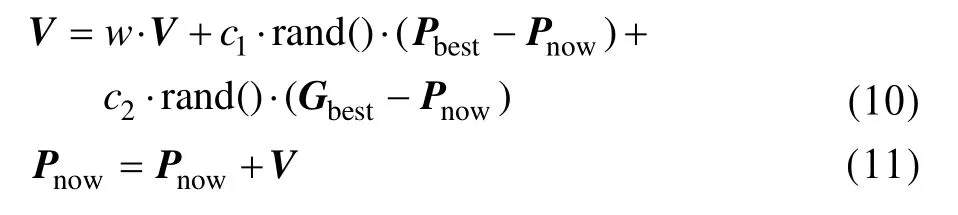
其中，V粒子速度；Pnow为粒子当前位置；Pbest和Gbest见前述定义；w加权系数，取值在0.1到0.9之间；rand()是(0, 1)之间的随机数；c1和c2称为学习因子，通常取2。

粒子通过不断的学习和更新，最终找到解空间中最优解所在的位置，整个搜索过程结束。最后输出的Gbest就是全局最优解。

粒子群优化算法结构简单、运行速度快，没有交叉和变异运算。但粒子群在搜索时有时会在全局最优解附近出现“振荡”，为了避免“振荡”的出现，做出如下改进[7]：随着迭代的进行，速度更新公式中的加权系数w由wini线性减小到wend，即：

其中，iter是当前迭代的代数；itermax是总的迭代次数。

4.2 非平滑非负矩阵分解的粒子群优化算法

基于 PSO 的约束的非负矩阵(Constrained Nonnegative Matrix Factorization, CNMF)算法[8]将顶点成分分析算法(Vertex Component Analysis, VCA)产生的结果作为该算法的初始值，但是VCA算法要求高光谱图像中至少存在每种端元的一个纯像元，实际中，这样的要求往往得不到满足，这样就降低了光谱解混的精度。PSO-CNMF算法利用 PSO同时对端元光谱矩阵和丰度矩阵进行搜索，然后通过 CNMF来更新，解空间维数相对较大，增加了计算复杂度，并且容易陷入局部最优值。真实高光谱图像中，一般图像的像元中不可能包括所有端元，只会包含其中的几种端元，导致丰度矩阵的稀疏性，但 PSO-CNMF算法不能很好搜索稀疏性矩阵解空间。

本文提出一种基于 PSO 的 nsNMF算法(PSO-nsNMF)，该算法采用 nsNMF输出的结果作为初始值，nsNMF算法没有VCA算法中纯像元的要求，更加接近真实情况。利用 nsNMF产生的初始值，可以有效避免 PSO的盲目搜索，提高找到全局最优值的概率。PSO-nsNMF算法利用PSO搜索端元矩阵，通过 nsNMF更新端元特征矩阵和丰度矩阵，相对于PSO-CNMF算法有效的缩小了解空间，降低了计算复杂度，提高了获得全局最优值的概率。PSO- nsNMF算法中 nsNMF引入“平滑”矩阵 C，可保证了更新过程中丰度矩阵的稀疏性，与PSO-CNMF算法相比，更符合真实情况。

在 PSO-nsNMF算法中，首先利用传统 nsNMF算法迭代得到的结果去初始化 PSO-nsNMF算法的M和S。然后通过粒子群优化产生的M和S让nsNMF算法进行迭代，产生的结果M送给PSO进行优化，重复整个过程直到找到全局最优值。

在PSO-nsNMF中的PSO部分，本文选择让M粒子群中每个粒子的位置，通过与元素在 0.002～0.005之间的随机矩阵相加增加粒子的多样性。粒子群中每个粒子的速度随机初始化。粒子群中每个粒子的最优值记为 PMi_best，粒子群的全局最优值记为 PMg_best，式(4)为适应值函数。

PSO-nsNMF算法的具体步骤如下：

(1)利用nsNMF算法输出的结果去初始化算法中的M和S。

(2)利用算法中的nsNMF部分去更新M和S，并输出结果。

(3)利用算法中的PSO部分去更新M，返回M的最优值 PMg_best和S的最优值 PSg_best。

(4)如果已经满足停止条件，则整个迭代过程结束，返回 PMg_best和 PSg_best。否则跳转到步骤(2)继续迭代。

5 实验与结果分析

5.1 合成数据实验

实验所用的模拟数据为 224波段 3端元模拟图像，是从USGS数字光谱数据库中选择的3个纯物质光谱，分别为光卤石、铵明矾石、黑云母。每种光谱都为224× 1维数据，其中224为光谱波段数。然后利用 Dirichlet分布[9]产生要合成的混合像元的丰度矩阵，大小为3× 1 296，其中1 296为要合成的像元的总数，并作归一化处理。为使得实验更具实效性，在合成数据中添加SNR为20 dB的随机噪声。实验分别比较标准 NMF、nsNMF和 PSO-nsNMF算法在合成数据中的结果。

对于标准NMF，M和S为随机初始值，但满足非负性和全加性约束。对于nsNMF算法，α和β分别为0和1，保证S的平滑性。θ取值为0.5保证一定的稀疏性。对于PSO-nsNMF、nsNMF算法产生的初始值作为粒子群的初始粒子。最大迭代次数设置为100，wini和wend分别设置为 0.9和0.4。学习因子c1和c2分别设置为 1.565和 1.565。

为评估 3种算法的有效性，利用光谱信息散度(Spectral Information Divergence, SID)和光谱角距离(Spectral Angle Distance SAD)来评估真实端元和估计端元之间的相似性，均方根误差(Root Mean Square Error RMSE)[1]来评估真实丰度值和估计丰度值之间的相似性。最后的量化结果通过 10次实验的平均值得到的，如表1所示。

表1 3个算法的准确性比较

从表 1可以看出，PSO-nsNMF所有指标均优于标准NMF和nsNMF，因此，通过PSO-nsNMF分解的混合像元的端元值和丰度值都更接近真实值。

5.2 真实数据实验

实验所用数据是 AVIRIS在美国 Cuprite地区[9]采集得到的真实高光谱数据集，本文选用大小为250×190像素的子图作为实验对象，如图1所示。在所有的224个波段中去除低噪声比和水蒸气吸收波段后(1～2, 104～113, 148～167和221～224)，剩余 188个波段[10]，即 L=188。

图1 美国Cuprite地区高光谱数据集(波段80)

利用虚拟维度[11]的方法确定这块图像中包含的端元个数为10，即P=10。通过与光谱库中的光谱对比得知这 10中端元分别为明矾石、榍石、白云母、绿脱石、镁铝石、胶岭石、蓝线、铁钙榴石、高岭石、水铵长石。在实验中选取白云母、榍石、明矾石3个典型的矿石作为例子来验证算法的有效性。

由标准 NMF、nsNMF和 PSO-nsNMF分解得到端元丰度结果见图2～图4，显示了3种矿石的端元分布图，可以看出由PSO-nsNMF得到的端元分布图比标准NMF和nsNMF得到的结果更接近真实值。

图2 白云母的丰度结果

图3 榍石的丰度结果

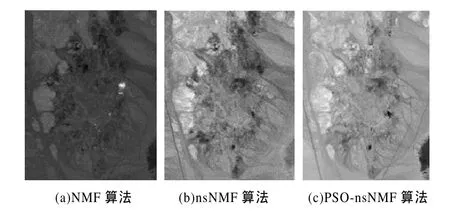
图4 明矾石的丰度结果

6 结束语

本文提出一种基于粒子群优化的非平滑非负矩阵分解的新算法 PSO-nsNMF，通过合成数据和真实的实验结果得知，PSO-nsNMF可以获得更好的全局最优解，其端元光谱和丰度值更接近真实值。下一步将研究如何更好地选取系数w、c1、c2、wini和wend，并改进算法结构，加强算法的全局搜索能力。

[1]贾 森.非监督的高光谱图像解混技术研究[D].杭州:浙江大学, 2007.

[2]Lee D D, Seung H S.Algorithms for Non-negative Matrix Factorization[C]//Advances in Neural Information Processing Systems.Denver, USA: [s.n.], 2000: 556-562.

[3]Montano A P, Carazo J M, Kochi K, et al.Nonsmooth Nonnegative Matrix Factorization(nsNMF)[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2006, 28(3): 403-415.

[4]Kennedy J, Ebethart R C.Swarm Intelligence[M].San Francisco, USA: Morgan Kaufmann Publishers, 2001.

[5]Keshava N, Mustard J F.Spectral Un-mixing[J].IEEE Signal Processing Magazine, 2002, 19(3): 44-57.

[6]Shi Yuhui, Eberhart R.Parameter Selection in Particle Swarm Optimization[C]//Proceedings of EP’98.London,UK: Springer-Verlag, 1998: 1958-1962.

[7]Shi Yuhui, Eberhart R.A Modified Particle S-Warm Optimizer[C]//Proceedings of Conference on Evolutionary Computation.Piscataway, USA: IEEE Press, 1998: 69-73.

[8]Cui Jiantao, Li Xiaorun.Unsupervised Hyperspectral Unmixing Based on Constrainted Nonnegative Matrix Factorization and Partcle Swarm Optimization[C]//Proceedings of GCIS’10.[S.l.]: IEEE Computer Society,2010: 376-380.

[9]Nascimento J M P, Dias J M B.Vertex Component Analysis: A Fast Algorithm to Unmix Hyperspectral Data[J].IEEE Transactions on Geoscience and Romote Sensing, 2005, 43(4): 898-910.

[10]基于非负矩阵分解的高光谱遥感图像混合像元分解[J].红外与毫米波学报, 2011, 30(1): 27-32.

[11]Chang C I, Du Qian.Estimation of Number of Spectrally Distinct Signal Source in Hyperspectral Imagery[J].IEEE Transactions on Geoscience and Remote Sensing, 2004,42(3): 608-619.