基于Petri网和混合蚁群算法的多星成像调度
2013-09-29龙运军陈宇宁陈英武邢立宁
龙运军,陈宇宁,陈英武,邢立宁
(国防科学技术大学信息系统与管理学院,长沙 410073)
1 概述
多星成像调度问题已被证明是NP-hard问题[1],人们至今未有较完善的解决方案。以往国内外的学者主要采用数学规划和图论的方法建模[2]。Petri网既是图形工具又是数学工具,具有图形直观、能描述冲突和并发、能以状态分布矩阵表示等优 点,是研究离散动态系统最有效的工具[3]。用Petri网表达具有多种约束和逻辑关系的优化问题,再结合现代优化方法求解,是一个值得研究的重要课 题。据目前掌握的资料,国内外尚未有采用 Petri网对多星成像调度问题建模的公开成果。本文通过在普通 Petri网中引入指标信息来克服数学规划模型直观性差和图论模型难以描述多星调度诸多约束的缺点,以直观有效地形式描述多星成像调度问题,特别是卫星资源争用和多星并发观测问题。
基于 Petri网调度问题的求解算法研究近年来受到了很多的关注。文献[4]提出一种通过Petri网和A*算法生成可行调度的方法;文献[5]探讨了基于 Petri网变迁序列编码的遗传调度优化算法;文献[6-7]探讨了 Petri网和混合算法相结合的优化方法。本文利用多星成像调度问题的邻域特性,在 Petri网中引入指标信息对多星成像调度问题进行描述,利用蚁群算法和局部搜索技术优化变迁序列,对多星成像调度问题进行求解。
2 相关符号说明
多星成像调度问题研究M颗卫星对N个任务实施侦察,已知各任务的时间窗口约束和相邻任务之间的侧摆转换时间约束,要求将卫星资源分配给各个任务使得观测总的收益值达到最大。
相关符号说明如下:
(1)观测任务集T={t1, t2,… ,tNT},卫星集合S={s1, s2,…,sNS},NT和NS分别表示待观测的任务总数和卫星总数。
(2)卫星sk对任务ti的时间窗为[W Ski,WEki],观测时间段为[Ski, Eki]。
(3)卫星sk最大侧摆Rk次,实际侧摆次数为rk,其侧摆速率为λ,侧摆后稳定时间为d。
(4)Okj表示卫星sk的第 j个观测活动,其观测时间段为[O Skj, O Ekj],侧摆角为Gj,nk为卫星sk观测活动总数。
(5)决策变量集X={ x1, x2,… ,xNT},且 ∀i∈{1,2,… ,NT},xi∈ {0,1}。 xi= 1表示任务ti被安排观测,xi= 0表示任务ti不被安排观测。
(6)任务集 T对应的观测收益集为P={ p1, p2,…,p NT}。
以最大化被安排观测任务的总收益值为调度目标,则该问题的目标函数可以表示为:

式(2)表示观测时间段必须在可见时间窗口内;式(3)表示受能量和存储量的限制,卫星实际侧摆次数不能大于其最大侧摆次数;式(4)表示相邻两次观测必须满足侧摆转换时间约束。
3 多星成像调度
Petri网在描述和分析离散事件动态系统中具有重要作用,因此,在多星成像调度问题建模中得到采用。
3.1 一类综合指标Petri网
在基于规则的系统控制与调度中,基本 Petri网难以有效反映系统外部的基于规则控制等因素,因此需要对其进行扩展。本文在基本 Petri网的基础上增加了能够影响系统进程的指标,定义了一类综合指标Petri网(Integrated Indexes Petri Net, IIPN)。
定义 综合指标 Petri网为一个五元组IIPN=(P, T, F, M , P r),其中:
(1)P为库所集合,T为变迁集合,F为流关系集合,且:

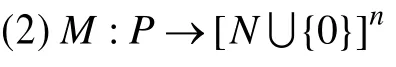
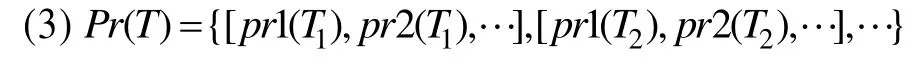
为与变迁相关的指标集合。
3.2 综合调度规则
以 IIPN为基础,根据以下规则可以构建多星成像调度问题的IIPN模型。
规则1 建立任务库所集合 Task={T1, T2,…,TN},其中,Ti是按照任务可见时间窗的先后顺序排列的,N表示任务总数,当托肯到达某个任务库所时代表该任务已完成成像活动。
规则2 任务库所集合中增加一个虚任务Tstart,并且把Tstart作为T1的前序任务。
规则3 设置一个变迁预处理阶段,在此阶段中利用遥感器侧摆转换时间约束消除所有无效变迁。
规则4 建立一个变迁序列:
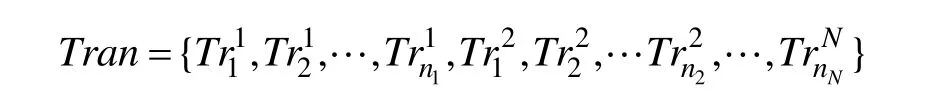
规则5 托肯代表当前观测方案,初始时刻,观测方案中没有任务,每当托肯到达一个任务库所,就把该任务添入观测方案中。
规则6 从一个任务库所到另外一个任务库所需要经过一个变迁,变迁的点火需要一个托肯和一个卫星资源库所的参与,变迁可包含多种指标,根据问题的特点和求解的需要设计指标信息。对指标的不同运用可以反映不同的调度需求,把指标综合在一起则是一种综合调度规则。
3.3 变迁指标设计
多星的短期调度具有2个重要特点:(1)多个任务竞争一颗卫星资源;(2)一个任务具有多颗卫星并发观测。可见,当任务规模较大时,多星成像调度问题是一个组合爆炸问题。针对多星成像调度问题的特点,为有效降低解空间的复杂度,提高解搜索的效率,设计如下变迁指标。
指标1任务收益值p。任务收益值表示任务一旦被观测可获得的收益,它反映了任务的重要程度,采用该指标可以有效解决卫星资源竞争问题,且本文将以观测方案的总收益值作为评价方案优劣的标准。
指标2 侧摆角slewAngle。侧摆角是卫星观测任务时星载遥感器偏离星下线的角度,侧摆消耗卫星能量,采用该指标可以有效解决多星并发观测的问题。图1所示为5个任务和2颗卫星的实例应用规则1~规则 5所构建的 IIPN模型。经过预处理阶段得到各任务的可见时间窗,可以通过甘特图来表示,卫星与任务之间的可见关系如图2所示。

图1 2颗卫星5个任务构建的IIPN模型
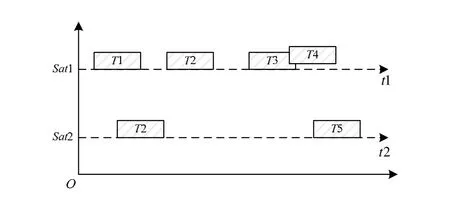
图2 卫星与任务可见关系甘特图
4 混合蚁群优化算法
在基本蚁群算法中,人工蚂蚁按照状态转移规则逐步构建可行解,它们将一些随机性引入到优化结果中,因此,基本蚁群算法很难快速地找到待优化问题的全局最优解。为提高求解效率,采用局部搜索技术来辅助蚁群优化过程。综合蚁群优化与局部搜索的方法已经成功运用于作业车间调度问题和带宽最小化问题等组合优化问题[8]。本文将混合基本蚁群算法和局部搜索技术求解多星优化问题。
4.1 信息素的定义和初始化
将“给定变迁被选择的概率”定义为方案空间上的信息素。用一个t×s维的矩阵Tao来记录信息素,t代表所有任务的个数,s代表所有卫星的个数。对于Tao中任意的元素τij,它的含义为选择用第 j颗卫星来观测第i个任务的概率。初始化阶段,信息素矩阵Tao中的元素都为0τ。
4.2 可行解的构造
4.2.1 构造机制
在构造可行解之前首先要根据卫星和任务的可见关系确定每个任务的变迁集合TR_set。然后将AntNum只蚂蚁放在初始节点Tstart处,在每一个解构造步,按照状态转移概率选择一个变迁,变迁实施后得到下一个任务,从而完成蚂蚁从当前任务到下一个任务的移动。每一只蚂蚁将实施过的变迁以序列的形式存储在当前路径中,并且放置一定数量的信息素在所选择的变迁上。当蚂蚁到达终止标识也就是最后一个任务Te时,就可得到一个从初始标识到终止标识的变迁实施序列,此即该蚂蚁找到的问题的可行解。
4.2.2 状态转移规则
从初始节点Tstart开始,对于每一任务Ti,按照以下的概率分布为该任务选择下一个需要实施的变迁:
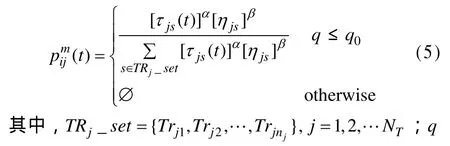
为[0, 1]之间均匀分布的随机数;q0为选择随机性参数。当 q≤q0时,按照信息素选择变迁;当q>q0时,∅按照如下的概率分布选择变迁:
其中,Pr(j, s, t)为t时刻为任务Ti选择变迁Trjs的概率。
4.2.3 启发式信息
概率选择是依据信息素强度τjs以及启发式信息ηjs的指引。在多星成像调度的IIPN模型中,变迁包含任务收益值p和侧摆角 slewAngle2个指标,本文将启发式信息ηjs设计为这2个指标的函数如下:收益值和侧摆角;、是本步骤可实施变迁集中所有可实施变迁的平均收益值和平均侧摆角。
其中,pjs、sajs分别为可实施变迁集 j中变迁Trjs的
4.3 信息素的更新
4.3.1 信息素的局部更新
在每次迭代完成后,本次迭代获得的最优调度的蚂蚁可应用局部更新规则来更新当前的信息素水平。局部更新规则基于本次迭代所获得的最优调度来完成对信息素的更新。更新方式如下:
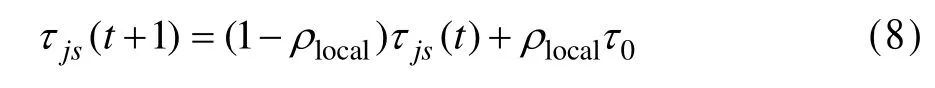
其中,ρlocal∈ (0,1)为局部信息素挥发系数。采用局部更新规则可以实现分化机制,避免算法过早陷入局部最优。
4.3.2 信息素的全局更新
在蚁群优化的迭代过程中,自开始迭代到当前迭代过程中获得全局较优调度的蚂蚁可以应用全局更新规则来更新当前的信息素水平。精英策略[9]选择一次迭代中的最优解完成信息素的更新,容易导致过早收敛。优化排序策略[10]将一次迭代中的解进行排序,根据位次加权更新信息素。本文采用最优解队列(Best Solution Queue, BSQ)进行全局更新,最优解队列中始终保持当前若干个最优解,若迭代过程中得到更优的解,则进行替换。每完成一次迭代后,更新最优解队列,同时应用全局更新规则更新信息素。全局更新方式如下:
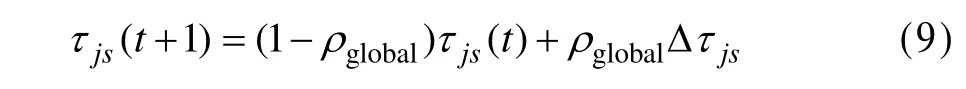
其中, ρglobal∈ (0,1)这里;Δτjs为信息素增量,其定义如下:

其中, Pl为蚂蚁l所走的变迁路径总收益;为所有任务的总收益值。
4.4 蚁群混合局部搜索
对于蚁群算法这样的群智能优化算法,全局搜索能力较强是因为每次迭代蚂蚁的搜索不是基于某种邻域结构的搜索,蚂蚁不需要被某种邻域结构所束缚。而缺点是一旦蚂蚁找到一个较好的邻域结构,一个较优的解甚至最优的解也许就在领域结构中,但蚂蚁却没有珍惜,从而导致迭代次数的大量增加。为此,本文在算法的每次迭代中加入局部搜索策略,混合局部搜索的算法取名为ACO-LS算法。
4.4.1 局部搜索
算法每次迭代完以后,对最优解队列 BSQ进行局部搜索。局部搜索基于给定解的邻域结构,采用插入未安排任务变迁和替换任务变迁的方法。插入未安排任务变迁就是将一个未安排任务变迁插入到某个已安排的任务变迁之后;替换任务变迁就是用未安排任务变迁来替换已安排任务变迁。用局部搜索后的最优解来更新最优解队列BSQ。
4.4.2 动态随机性参数
局部搜索可以有效加速收敛。蚁群算法的主要任务在于提高全局搜索能力,以发现更好的邻域结构。本文给随机性参数q0设定一个阈值。如果当前最优解连续σ次迭代没有改进,随机性参数取0lq,以增大其对变迁选择的随机性,直到其出现更优的解,随机性参数取q0h,以辅助加速收敛。
4.4.3 混合蚁群算法的优化流程
蚁群混合局部搜索的优化流程如图3所示。
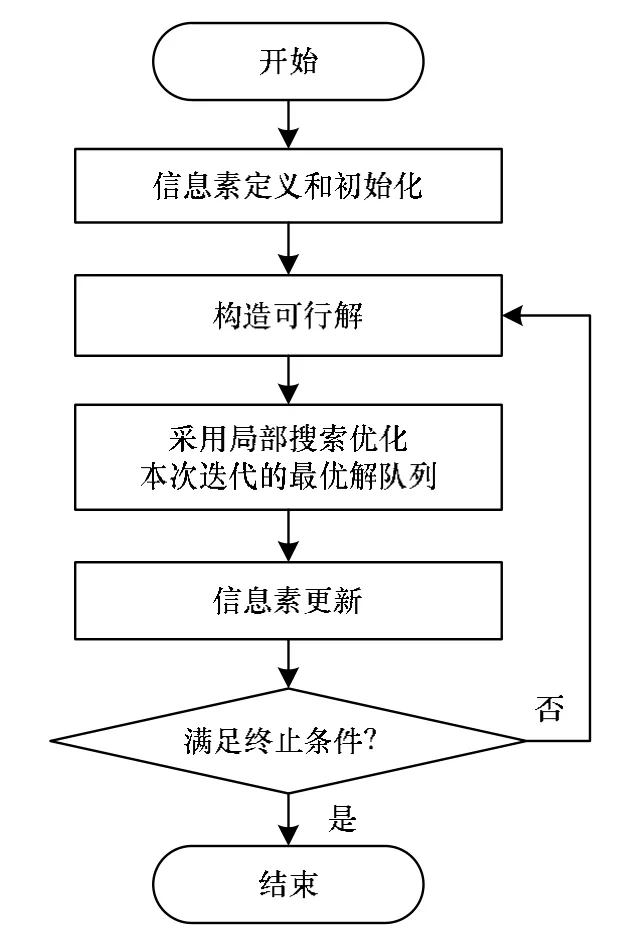
图3 蚁群混合局部搜索的优化流程
4.5 终止条件
多星成像调度问题的目前还没有标准的测试实例,而且在实际的工程应用中问题规模是随机的,因此问题的最优调度解通常是未知的。本文以预设的最大迭代次数作为算法的终止条件。
5 仿真实例与分析
目前,在卫星调度领域,还没有公认的测试集,常见的做法是采用随机生成任务方法验证算法,仿真实例生成规则如下:
(1)在区域(北纬[20°, 50°],东经[70°, 130°])内按照均匀分布生成点目标,并忽略任务对遥感器的类型要求及分辨率要求。目标数量 M取值为{100,200,300}。
(2)卫星数量取值为{3,4,5}。
(3)任务收益值从[1,10]之间随机生成。
(4)任务与卫星的时间窗口采用STK软件生成。
ACO-LS算法的参数设置如表1所示,算法均采用C#实现,编译环境为VS.net 2005,实例在配置为Core(TM)i3 2.93 GHz CPU,2 GB内存的计算机上运行。
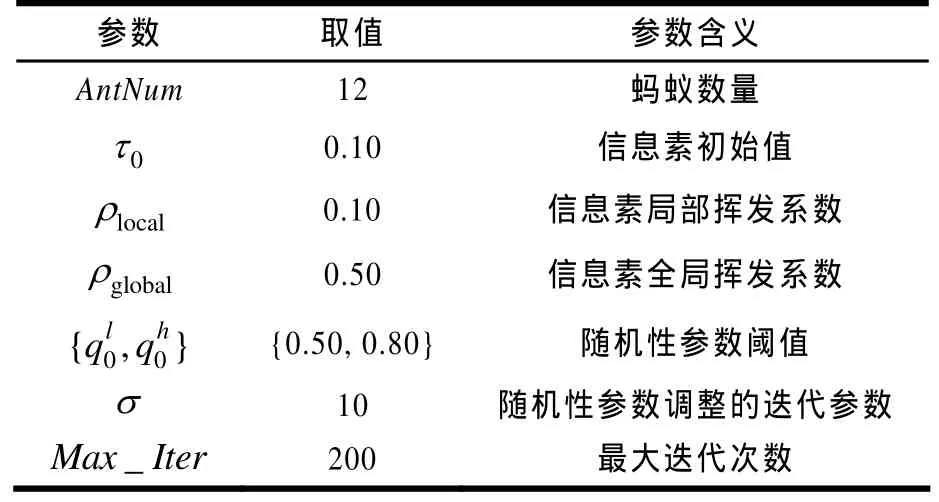
表1 ACO-LS算法的参数设置
5.1 模型与算法有效性测试
以多星成像调度问题的约束满足模型为基础,文献[11]采用禁忌搜索算法求解。为验证本文模型和算法性能,将本文求解结果与其进行比较。每个算例在2种算法上各运行10次,结果取10次的均值,计算结果如表 2所示。其中,算例名称表示目标数-卫星数;OBS为经轨道预报后,算例中任务的总时间窗口数量;RESULT为计算结果;CPU为计算时间,GAP为运行结果与TS算法相比提高的效率。
从各测试算例的计算结果来看,本文将 Petri网和 ACO-LS相结合的方法均对基于约束满足模型的TS算法的结果有所改善。当问题规模增大时,本文方法对求解结果改善更可观。但第3个算例的求解结果没有改善,究其原因是卫星资源丰富,可见时间窗口很多,任务完成率高,采用本文方法的优势不明显。通过算例比较,表明基于Petri网和ACO- LS的多星成像调度方法可行,且求解结果较优。
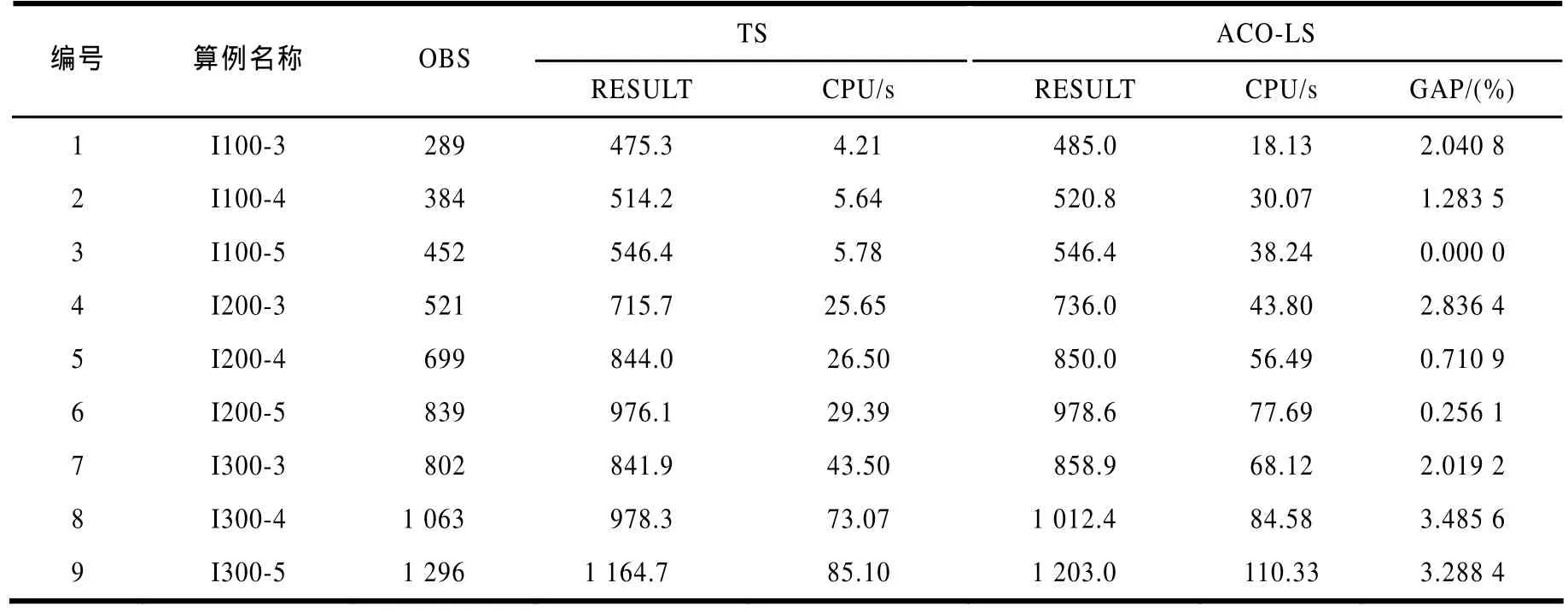
表2 2种算法的求解结果比较
5.2 变迁指标对结果的影响
多星成像调度的 IIPN模型中的变迁包含任务收益值p和侧摆角slewAngle 2个指标,在ACO-LS算法中2个指标通过启发式信息ηjs发挥作用。
为测试2个指标对算法性能的影响,针对实例5和实例9,分别在取一个指标和取2个指标的情况下计算,各次迭代得到的最佳结果的进化情况如图 4所示。
可以看出,启发式信息若只考虑侧摆角,则收敛速度很慢,且解的质量很差,那是因为算法着重处理了多星并发观测的情况却忽略了对竞争情况的处理。
若只考虑任务收益值,虽然解得质量比只考虑侧摆角时要好,但是收敛速度仍然很慢,其原因同样是缺乏系统的考虑,偏重处理竞争情况。
若同时考虑这2个指标,算法的性能则有很大的改善,同时可以看出,2个实例分别在第 50次和第80次迭代时就已经取得最优解了。
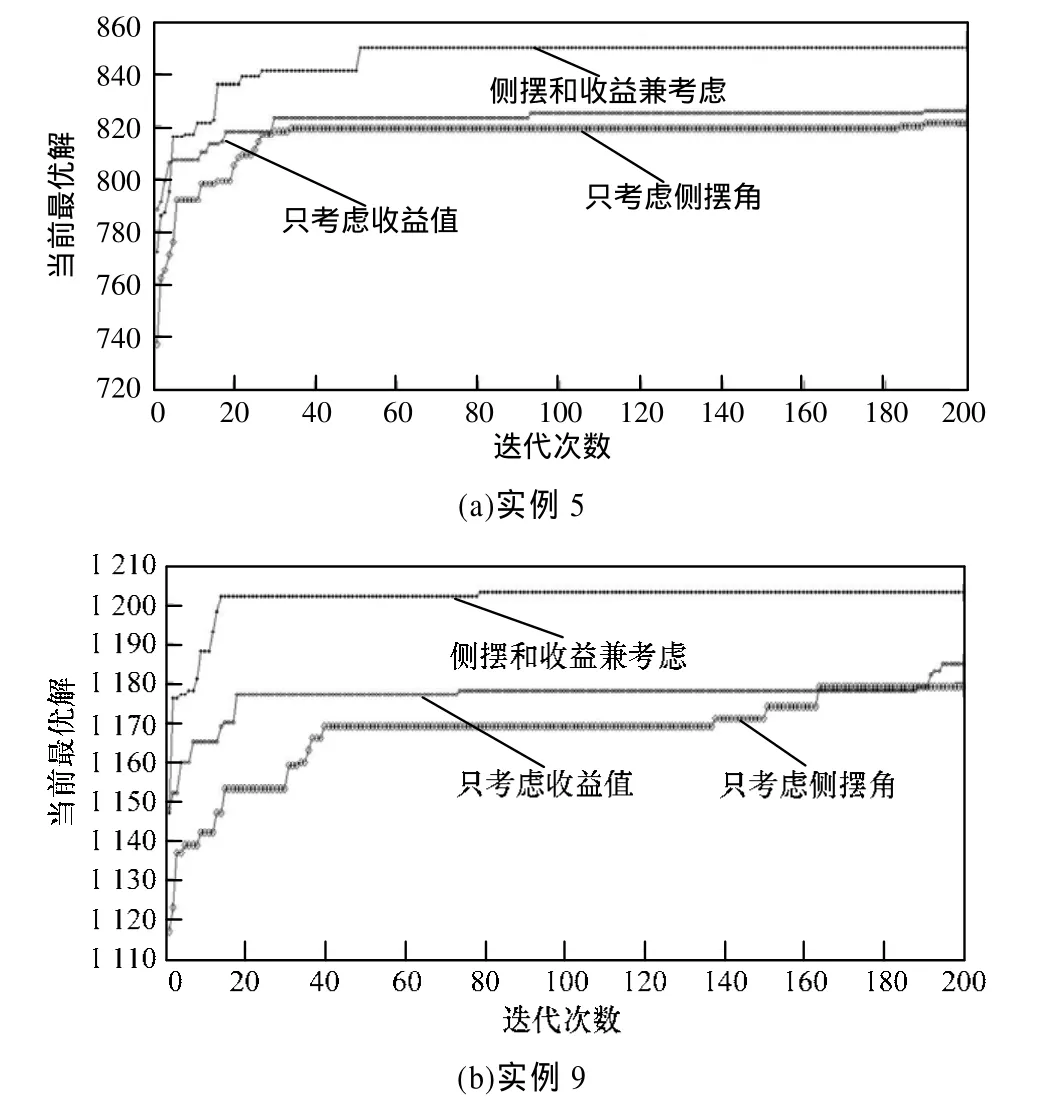
图4 2个实例的最佳结果进化情况
6 结束语
多星成像调度问题是一个典型的NP-Hard问题,国内外学者从不同角度对其进行了建模和求解。本文针对多星成像调度问题的特点,提出基于综合指标Petri网和混合蚁群算法的多星成像调度策略,并给出一种ACO-LS算法。仿真结果表明,将本文策略运用于求解多星成像调度问题是有效的,优于文献[11]所采用方法的求解结果。在卫星和任务数量相对较多时,当前基于 Petri网的方法对多星成像调度问题的描述相对复杂。后续研究中需要对该策略进行改进或寻求新的描述方法,以对问题进行更简洁、直观的描述。
[1]Bensana E, Verfaillie G, Bataellie N, et al.Exact and Approximate Methods for the Daily Management of an Earth Observing Satelete[C]//Proc.of SpaceOPS’96.Munich, Germany: [s.n.], 1996.
[2]贺仁杰, 李菊芳, 姚 锋, 等.成像卫星任务规划技术[M].北京: 科学出版社, 2011.
[3]袁崇义.Petri网原理与应用[M].北京: 电子工业出版社,2005.
[4]Lee D Y.Scheduling FMS Using Petri Nets and Heuristic Search[J].IEEE Trans.on Robotics and Automation, 1994,10(2): 123-132.
[5]郝 东, 蒋昌俊, 林 琳.基于 Petri网与 GA 算法的FMS调度优化[J].计算机学报, 2005, 28(2): 201-208.
[6]肖良清, 乐晓波.时间Petri网与遗传蚁群算法相结合的并行测试研究[J].系统仿真学报, 2009, 21(23): 7648-7654.
[7]潘全科, 朱剑英.基于Petri网和混合算法的作业车间优化[J].计算机集成制造系统, 2007, 12(3): 580-584.
[8]Blum C.Beam-ACO Hybridizing Ant Colony Optimization with Beam Search: An Application to Open Shop Scheduling[J].Computers and Operations Research, 2005,32(6): 1565-1591.
[9]Dorigo M, Stuzle T.Ant Colony Optimization[M].[S.l.]:MIT Press, 2004.
[10]Bullnheimer B, Hard R R, Strauss C.A New Rand-based Version of the Ant System: A Computational Study[J].Central European Journal for Operations Research and Economics, 1999, 7(1): 25-38.
[11]贺仁杰.成像侦察卫星调度问题研究[D].长沙: 国防科学技术大学, 2004.
