基于多线程技术的分辨函数析取范式生成算法
2013-09-29蒙祖强周石泉黄柏雄
蒙祖强,周石泉,黄柏雄
(广西大学计算机与电子信息学院,南宁 530004)
1 概述
Rough集理论[1]经过30年的发展,在模式识别、图像处理和数据挖掘等领域已发挥重要的作用[2]。属性约简是Rough集理论的核心内容之一,目前大量的研究工作主要集中在属性约简方面。属性约简主要有2种方法,一种是通过数据依赖性分析来计算属性的重要性,然后由此计算满足特定需求的约简[3-4],这是一种相对成熟的方法,其复杂度已经降低至线性复杂度;另一种方法是通过创建分辨矩阵来构建分辨函数,然后将分辨函数转化为析取范式,从而求取所有的约简[5]。后者的优点是:其设计过程简单明了,便于编程实现,且可以求取一个信息系统的所有约简,因而被广泛采用。但目前其指数级的时间复杂度[5]仍然未能得到根本性的降低,因而不适用于海量数据的约简。这主要是因为将分辨函数从合取范式转化到析取范式的过程中存在组合爆炸问题。目前,仍然没有解决这种组合爆炸的有效方法,通常是从局部上采取一些改进措施,在一定程度上降低这种复杂度。例如,文献[6]提出基于二分法技术的范式转化方法,在一定程度上降低计算复杂度。文献[7]给出了一种矩阵转换的直接搜索方法,但在转化过程中没有充分地利用吸收律,导致产生大量的冗余项,影响了算法效率。文献[8]提出一种模拟人工转换的范式转换算法,该算法的实现过程简单明了,但它未能有效吸收二分法技术的设计思想来进一步降低其计算复杂度,其效率可进一步提高。
由于合取范式中的合取运算是满足结合律和交换律的,因此可以对合取范式中的析取式进行分组,然后对各组并行进行析取范式转化,接着进行分组、再进行并行析取范式转化,直到获得最终的析取范式。显然,这是一种并行计算模式。同时由于当前多核计算机以其独有的优势[9],日益受到用户的青睐,多核CPU电脑的出现已经十分普遍,而单线程的程序难以充分发挥多核CPU的功能。因此,在多核CPU环境下,基于上述的并行模式用多线程技术来加快析取范式的转化就显得十分有意义。
本文指出范式转化与约简计算之间的关系,导出范式转化的并行模型,由此提出基于多线程技术的析取范式生成算法,并通过实验对本文算法进行有效性验证。
2 信息系统和分辨函数
在Rough集理论中,信息系统是数据的逻辑表示方式。一个信息系统(Information System, IS)可表示为四元组:IS=
对于一般的信息系统而言,分辨矩阵中的元素mij是表示能区分对象xi和xj的所有属性的集合;对于决策系统而言,元素 mij也表示能区分对象 xi和xj的所有属性的集合,但其前提是对象 xi和 xj的决策值不同,即fd(xi)≠fd(xi),否则令mij=φ。具体地,假定U={x1, x2, …, xn},对于给定的信息系统IS=
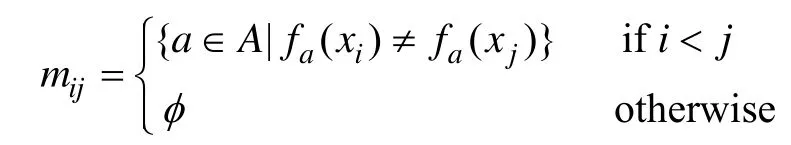
对于给定的决策系统DS=
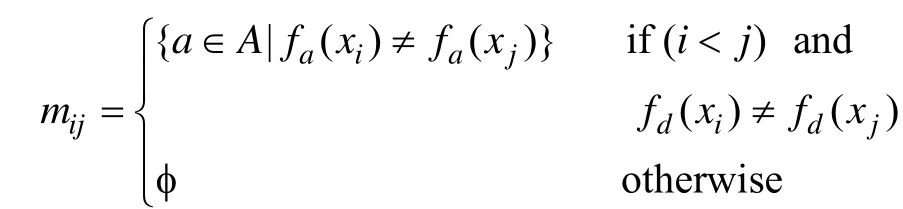
其中,i,j∈{1,2,…,n}。
元素mij中的任一属性都可以区分对象xi和xj,因此,这些属性之间的关系是或的关系(析取),而元素mij之间的关系是与的关系(合取)。这样,可以构造如下的合取范式:F(S)=∧(∨mij), mij≠φ。其中,∨mij表示由 mij中的所有属性构成的析取式,所有这样的析取式的合取便是 F(S)。F(S)是一个合取范式,称为F(S)为信息系统或决策系统的分辨函数,S表示IS或DS。当将F(S)从合取范式转化为析取范式,便得到对应系统的所有约简[5]。显然,不管是信息系统还是决策系统,它们的分辨函数并无本质上的区别。
考虑如表1所示的决策系统DS=

表1 决策系统
先构建其分辨矩阵,然后构造其分辨函数,结果如下:

将以合取范式表示的分辨函数转化为析取范式:
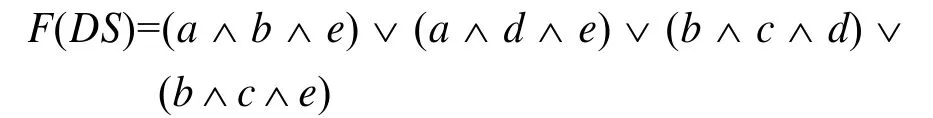
由此可知,该决策系统的所有约简包括:{a, b,e},{a, d, e},{b, c, d},{b, c, e}。
3 范式转化的并行模型
合取范式是由若干个简单析取式通过合取联结词连接而成的逻辑公式。将这种简单析取式简称为析取项;析取项中属性的个数称为析取项的长度;析取项的个数称为合取范式的长度;如果对一个合取范式已经充分应用了吸收律,则该合取范式是极小的合取范式。对于析取范式,也可以平行地定义相应的概念:合取项,合取项的长度,析取范式的长度,极小的析取范式。
由此可见,程序在扫描数据集时可直接生成以合取范式表示的分辨函数,而不需要生成分辨矩阵。问题的关键是,如何将以合取范式表示的分辨函数高效地转化为析取范式。这种转化过程遇到最大的困难就是组合爆炸问题。但是,在创建分辨函数和析取范式转化时充分应用吸收律,可以大幅度降低析取项和合取项的数量。当然,吸收律的应用并不能从根本上解决组合爆炸问题,而只能从局部上提高算法的效率。
对于合取范式,由于合取运算满足结合律和交换律,因此可以对析取项进行任意的组合,然后对各组合同时进行合取分配运算,所得的结果都是一样的。这为转化的并行化操作提供了理论基础。
一般地,假设在扫描数据集后得到的极小合取范式具有形式:I1∧I2∧…∧In。然后按照结合律和交换律,对这n个析取项进行分组,假设得到m个组,并对各组进行并行运算,之后各组都是子析取范式。为方便讨论起见,假设 m=2k,即 m为 2的k次幂,k为一正整数。这样将该合取范式并行转化为极小析取范式的计算模型可以用图1表示。

图1 析取范式转化的并行模型
在图1中,各层上的每个结点代表一个逻辑运算单元及其运算结果(子析取范式)。除了第 0层上的结点表示对最初的各分组进行运算及其结果以外,其他层上的结点都是表示对其2个孩子结点的运算及其结果。为了有效实施同步控制,约定:同一层上的结点可以并行执行运算,且当前层上的结点都运算完后下一层上的结点才能开始进行运算。这样同一层上各结点的负载平衡就显得特别重要。通过计算2个子析取范式的长度的乘积来估计结点的负载程度,从而决定结点的组合。也就是说,结点的组合不是基于结点相邻的原则,而是根据负载平衡的原则进行。
4 基于多线程技术的析取范式生成算法
并行模型的实现需要并行环境。但如果没有真正的并行环境,可以利用现在电脑普遍提供的多核CPU环境来实现该并行模型。Windows操作系统虽然能够自动在多核上分配计算任务,但这种分配操作主要是基于线程的,线程是CPU的调度单位。因此,需要将计算任务分为若干个线程的计算,这样才能充分利用多核CPU提供的资源,实现一定程度上的并行计算。
基于上述考虑,在图1的并行模型中,每个结点的计算任务就可以用一个线程来完成,即一个结点对应一个线程,一旦计算结束就销毁线程。线程之间没有直接通信,但所有线程都共享一个结构体数组,该结构体数组存放着各个时期计算形成的子析取范式所在内存块的首地址和该子析取范式的长度。多个线程可同时访问该数组的不同元素。假设该结构体数组为 Q[],Q[i].addr表示当前第 i+1个子析取范式所在内存块的首地址,Q[i].size表示当前第 i+1个子析取范式的长度。在一个线程执行对第i+1个子析取范式和第 j+1个子析取范式的逻辑分配和吸收运算后,会得到一个新的子析取范式,将它所在内存块的首地址和它的长度分别存放到Q[i].addr和 Q[i].size中,而 Q[j].addr和 Q[j].size分别置为 NULL和 0。当并行模型中当前层上的结点对应的线程都执行结束以后,删除 Q[i].addr为NULL的结构体并按照Q[i].size的大小对Q[]中的元素进行升序排列,这2个操作分别称为Q的缩小和排序。在对当前的Q进行缩小和排序后,假设其长度 pQ;然后对当前的子析取范式进行下列的组合(称为首尾组合):(Q[0].addr, Q[pQ–1].addr),(Q[1].addr,Q[pQ–2].addr),(Q[2].addr, Q[pQ–3].addr),…,(Q[p Q/2–1].addr, Q[pQ–p Q/2].addr)。这样的组合是出于实现负载平衡的需要。当然,这不是最佳的负载平衡方案。但如果过多地追求负载平衡,可能会大量增加计算时间。因此,暂且采用这种相对简单的负载平衡解决方法。
根据以上分析,并考虑到合取范式到析取范式的转化是计算一个信息系统所有约简的关键,同时也是最耗时的过程,因此,下面只给出合取范式到析取范式转化的算法,该算法是利用多线程技术来实现图1所示的并行模型。
基于多线程技术的析取范式生成算法如下:
输入 以合取范式表示的分辨函数F(S)
输出 极小的析取范式
Step1 对F(S)充分运用吸收律,将之转化为极小的合取范式,结果保存在结构体数组Q[]中。
Step2 将Q[]中的子析取范式分成ThreadN个组,然后启动 ThreadN个线程,并行执行对这 ThreadN个组的析取范式转化 //ThreadN表示最大线程数。
Step3 对Q进行缩小和排序,并进行首尾组合。
Step5 当Step4中的线程都执行结束后,对当前的Q进行缩小和排序 //这时pQ约缩减为原来的1/2。
Step6 如果这时 pQ等于 1,则转 Step7,否则对 Q进行首尾组合,然后转Step4。
Step7 返回Q[0].addr所表示的析取范式。
5 实验分析
为验证基于多线程技术的析取范式生成算法(记为算法1)的性能,做了相关的实验对比和分析。首先,将算法1中的线程去掉,改用函数来代替线程完成相应的功能。这样,算法 1的循环部分(Step4~Step6)就变为串行执行,由此修改得到的算法记为算法2。在实验中,一共随机生成11条不同的合取范式,合取范式的长度从 150~250(间隔为10,如表2所示),可能出现的属性一共有20个。

表2 随机生成的合取范式基本信息
在表2中,“A”代表合取范式的长度(析取项的个数);“B”代表合取范式中属性出现的总次数;“C”代表合取范式中析取项的平均长度(各析取项平均包含的属性个数),即C=B/A。
实验是在 Rentium Dual-Core CPU(双核 CPU)、主频2.7 GHz、2 GB内存的机器上完成,操作系统是Windows XP。算法1中的参数ThreadN被设置为100。算法1和算法2执行后分别产生相同的结果,表3列出了这些析取范式的基本信息。但它们的运行时间的变化趋势却有明显差别,如图2所示。
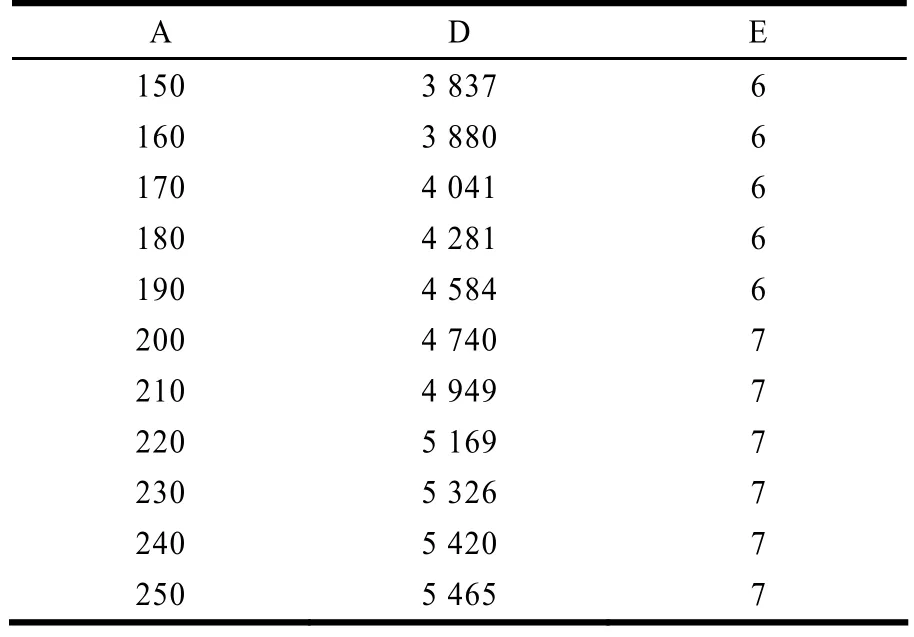
表3 析取范式基本信息
在表3中,“A”的意义同表2;“D”代表产生的析取范式的长度(合取项的个数,即约简的个数);“E”代表析取范式中合取项的平均长度(即约简的平均长度)。

图2 算法运行时间
从图2可以看出,当合取范式长度比较小时,2种算法的运行时间的差别并不大,但随着合取范式长度的增加,这种差别就越来越明显。究其原因,认为当合取范式的长度增加时,就有更多的线程参与运算,从而提高算法1的执行效率。这说明当合取范式中析取项的个数比较大时,算法1在执行效率上会明显优于算法2,这时应该选择算法1。对于实际决策系统来说,其分辨函数的长度一般都比较大,而且算法1只利用了当前电脑普遍配置的多核CPU环境,因此,算法1在工程应用中具有明显的实际意义。
6 结束语
基于Skowron矩阵计算信息系统所有约简是一个 NP难问题。本文虽然不能从根本上解决这个问题,但利用当前电脑普遍提供的多核CPU环境和多线程技术,设计了基于多线程技术的析取范式生成算法,可以在局部上进一步提高析取范式的转化效率,这在实验中得到了有效的验证。由于本文算法只需在当前普遍使用的多核CPU电脑上运行,因此具有一定的推广价值和应用前景。
[1]Pawlak Z.Rough Set[J].International Journal of Computer and Information Sciences, 1982, 11(5): 341- 356.
[2]王国胤, 姚一豫, 于 洪.粗糙集理论与应用研究综述[J].计算机学报, 2009, 32(7): 1229-1246.
[3]徐章艳, 刘作鹏, 杨炳儒.一个复杂度为 max(O(|C||U|),O(|C|2|U/C|))的快速属性约简算法[J].计算机学报, 2006,29(3): 391-399.
[4]Meng Zhuqiang, Shi Zhongzhi.A Fast Approach to Attribute Reduction in Incomplete Decision Systems with Tolerance Relation-based Rough Sets[J].Information Sciences, 2009, 179(6): 2774-2793.
[5]Skowron A, Rauszer C.The Discernibility Matrices and Functions in Information Systems[M]//Slowinski R.Intelligent Decision Support: Handbook of Applications and Advances of the Rough Sets Theory.Dordrecht,Netherlands: Kluwer Academic, 1992: 331-362.
[6]王元珍, 裴小兵.基于Skowron分明矩阵的快速约简算法[J].计算机科学, 2005, 32(4): 42-44.
[7]赵荣泳, 张 浩, 李翠玲, 等.粗糙集理论中分辨函数的析取范式生成算法[J].计算机工程, 2006, 32(2): 183-185.
[8]张德栋, 李仁璞, 赵永升.一种高效的分辨函数范式转换算法[J].计算机应用研究, 2010, 27(3): 879-882.
[9]李 斌, 李海玉, 孙延君.多核计算机上的并行计算[J].电脑编程技巧与维护, 2011, (18): 57-59.
[10]Zhao Kai, Wang Jue.A Reduction Algorithm Meeting Users’ Requirements[J].Journal of Computer Science and Technology, 2002, 17(5): 578-593.
