基于四元数的双彩色图像盲水印算法

姚 涛，苏庆堂，阙大顺

(1.鲁东大学信息与电气工程学院，山东 烟台 264025；2.武汉理工大学信息学院，武汉 430063)

1 概述

随着数字多媒体技术的发展，数字水印技术被认为是解决版权问题的一种有效方式[1]。图像水印的相关研究成果已经很多，但大多集中在灰度图像水印技术。计算机技术、通信技术和多媒体技术的发展使得在实际应用中彩色图像占据了主导地位，而关于这方面的研究成果却很少，其中比较典型的算法[2-4]有：

(1)单通道法：根据人眼对RGB颜色模型中蓝色分量变化不敏感的特性，通过修改彩色图像的蓝色分量值或对其变换到变换域，在变换域中嵌入水印信息；或把彩色图像由 RGB颜色模型变换到 YUV或YCbCr颜色模型，然后在人眼不敏感的亮度分量中嵌入水印。这类算法保证了水印的不可见性，但是嵌入的水印信息量较少。

(2)多通道法：对彩色图像R、G、B 3个分量分别做离散傅里叶变换(Discrete Fourier Transform,DFT)、离散余弦变换(Discrete Cosine Transform,DCT)、离散小波变换(Discrete Wavelet Transform,DWT)和 Contourlet变换后，把水印信息嵌入到频域系数中[5-6]。虽然这类算法可以把水印扩展到整幅图像中，但还是把像素的各个分量分离了，没有考虑到像素各个分量之间的联系，而且算法需要对彩色图像的各分量分别做变换和嵌入，计算量较大。

四元数理论在图像处理、人工智能、计算机视觉、模式识别等领域有着广泛的应用[7-10]。近年来，四元数理论在彩色图像处理方面的应用尤为突出。四元数分为实部和虚部两部分，其中，虚部又分为i、j、k 3个部分，可以使彩色图像的 R、G、B 3个分量作为这3个虚部分量，而四元数的实部为0。此时进行基于四元数的离散傅里叶变换，算法始终将彩色像素作为一个整体来处理，在具有良好的不易感知性的同时，也保证了算法的鲁棒性。

本文提出一种基于四元数理论的双彩色图像水印算法，通过对彩色宿主图像和水印图像分别进行离散四元数傅里叶变换(Discrete Quaternion Fourier Transform, DQFT)得到其频谱，并置乱水印图像频谱系数，然后根据DQFT的特性，选择适当的频域系数进行彩色水印图像的嵌入。

2 四元数

四元数可以看成是复数的推广，它包括1个实部和3个虚部，也称为超复数，可视为特殊的clif-ford代数，近年来在图像处理中得到广泛的应用。

一个四元数可表示为：

其中， a0r,a1, a2,a3∈R；3个虚数i、j、k满足：

四元数q还可用幅值和相位表示为：

一幅大小为 M×N的 RGB彩色图像 f( m, n),m ∈ [0,M − 1], n ∈ [0,N − 1]用四元数表示为：

其中，实部 fr(m, n) =0；fi( m, n)为R分量；fj(m, n)为G分量；fk(m, n)为B分量。

由式(2)可以看出，四元数的乘法不满足交换律。因此，图像处理中常用的离散傅里叶变换的四元数有3种定义形式[11]：

(1)双边变换

(2)左边变换

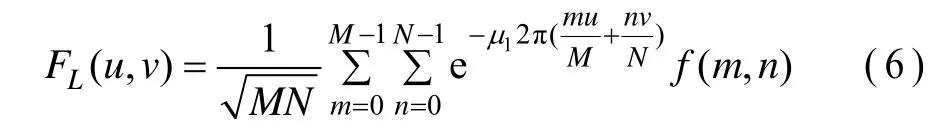
(3)右边变换

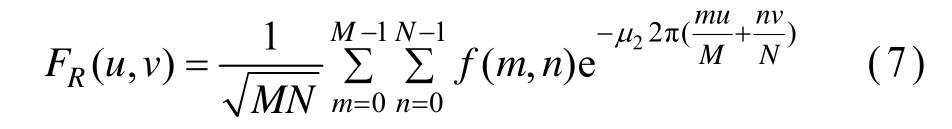
四元数傅里叶变换中需要2个独立的iμ，且计算量明显大于单边DQFT，迄今为止还没有数据表明这2类变换的优劣，因此，本文算法采用左变换来实现。

左边变换对应的逆变换定义为[12]：

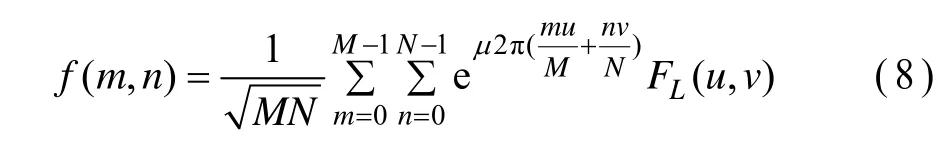
其中，μ为单位向量；(u, v)和(m, n)分别为频域和时域中的坐标。

这里把 f( m, n)称为空间域，F( u, v)称为频率域，F( u, v)也是一个四元数，可表示为：

3 水印图像预处理

混沌序列是一种伪随机序列，具有各态历经性、非周期性、宽频谱性等特点，所以，用它加密的信息很难破译，能大大提高算法的安全性。混沌序列易生成，对初始条件敏感，初值产生很小的变化即会产生完全不同的混沌序列。因此，混沌被广泛应用于信息的置乱、加密和隐藏领域。

常见的Logistic混沌序列具有以下优点：

(1)序列的统计特性等同于白噪声。

(2)只需要混沌映射参数和初始条件就可重现混沌序列，因此，不必浪费空间存储整个混沌序列。

(3)利用混沌系统对初始条件的敏感特性，可获得数量很多的混沌序列。

(4)几乎不可能从有限长数据中推断出混沌序列的初始条件，因此，无法解密，而这对信息安全非常重要。

4 嵌入及提取算法

4.1 嵌入算法

水印的嵌入过程分为以下3步：

(1)分别选取合适的参数 μ对 I（ x, y） 和 W（ m , n）做DQFT变换，得I( u, v)和W( u, v)。

(2)利用混沌序列分别对水印图像变换后的低频、中频和高频系数做置乱处理，得到置乱后的系数W′( u, v)。

(3)在频域 I（ u, v） 中嵌入W′( u, v)，为了减小嵌入强度对透明度的影响，在嵌入水印时采用脉冲编码调制(Pulse Code Modulation, PCM)中的方法实现系数的量化。

嵌入过程如下：

首先利用量化的方法对W′( u, v)系数进行 8位量化编码，再把编码每个量化后的8位系数分为4组，每组 2位(为了描述方便，记为 bibj)。在低频系数、中频系数和高频系数中选择合适的频域系数分别嵌入水印的低频系数、中频系数和高频系数的4组编码数据，把载体图像频域 I（ u, v）系数C量化到最近的数值。具体算法如下：

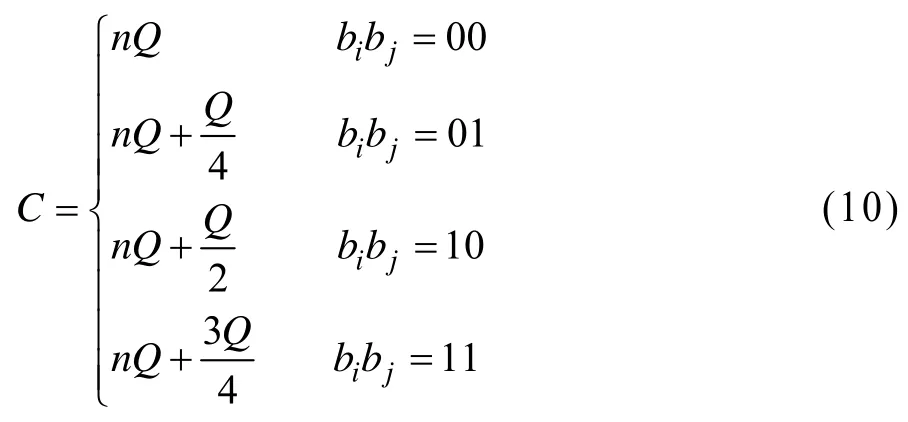
其中，Q可根据低频、中频和高频系数的大小分别取不同的量化值，由此得到嵌入水印后图像的频域I′（u, v） 。

(4)对 I′（u, v）做反 DQFT变换得到的空域图像I′（x, y） 即为嵌入水印后的图像 I ′（x, y） 。

4.2 提取算法

提取算法为嵌入算法的逆过程，如图1所示。

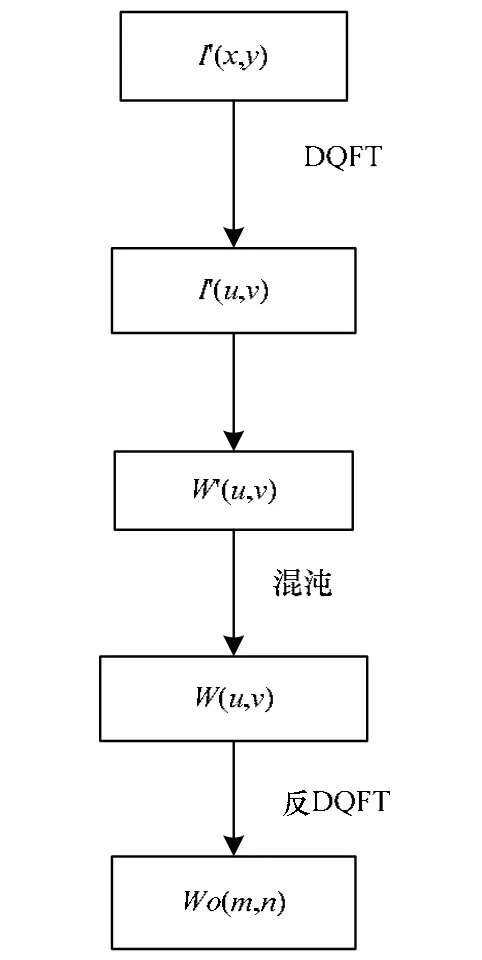
图1 水印提取过程

5 实验结果与分析

本文利用Matlab7.0进行仿真实验。原始载体图像为 512×512像素的彩色 Lena图，如图 2(a)所示，水印图像为 64×64像素的彩色 baboon图，如图 2(b)所示，参数Q=16，嵌入水印后的图像如图2(c)所示。无攻击时提取水印图像，实验结果如图2(d)所示。

实验中采用峰值信噪比PSNR来定量分析算法的性能，PSNR定义如下：

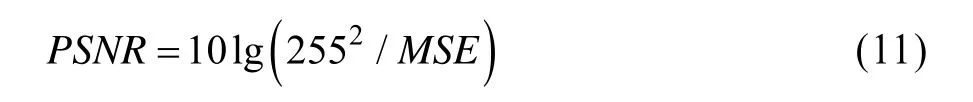
其中，X是原始载体图像；Xw是嵌入水印后的图像；MSE是均方误差计算公式：

其中，M、N分别是图像的高和宽。PSNR值越大，说明隐藏信息的透明性越好。

本文采用归一化相似度NC定量评价算法的鲁棒性，NC的定义如下：

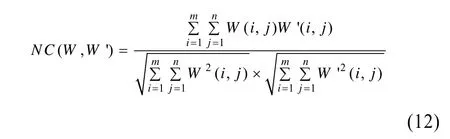
其中，Q值分别取低频、中频和高频系数分量均值的0.06倍、0.08倍和 0.12倍，嵌入水印的图像的PSNR=38.025 3，无攻击时提取水印的NC=0.999 8。

攻击测试实验结果如表1所示。从中可以看出，本算法可以在各频率分量自适应地嵌入水印，在低频分量嵌入水印的低频分量，在保证算法不可见性的同时，提高了算法的鲁棒性。低频分量集中了图像的大部分能量，在此嵌入水印，鲁棒性较高，所以，本文算法嵌入水印图像的低频分量，提高了算法的鲁棒性。而中频分量和低频分量能量相对较少，嵌入强度加大，也提高了算法的鲁棒性。因此，与传统水印算法相比，本文算法嵌入容量较大，并且在保证不可见性的同时，对常见的攻击具有较强的鲁棒性。

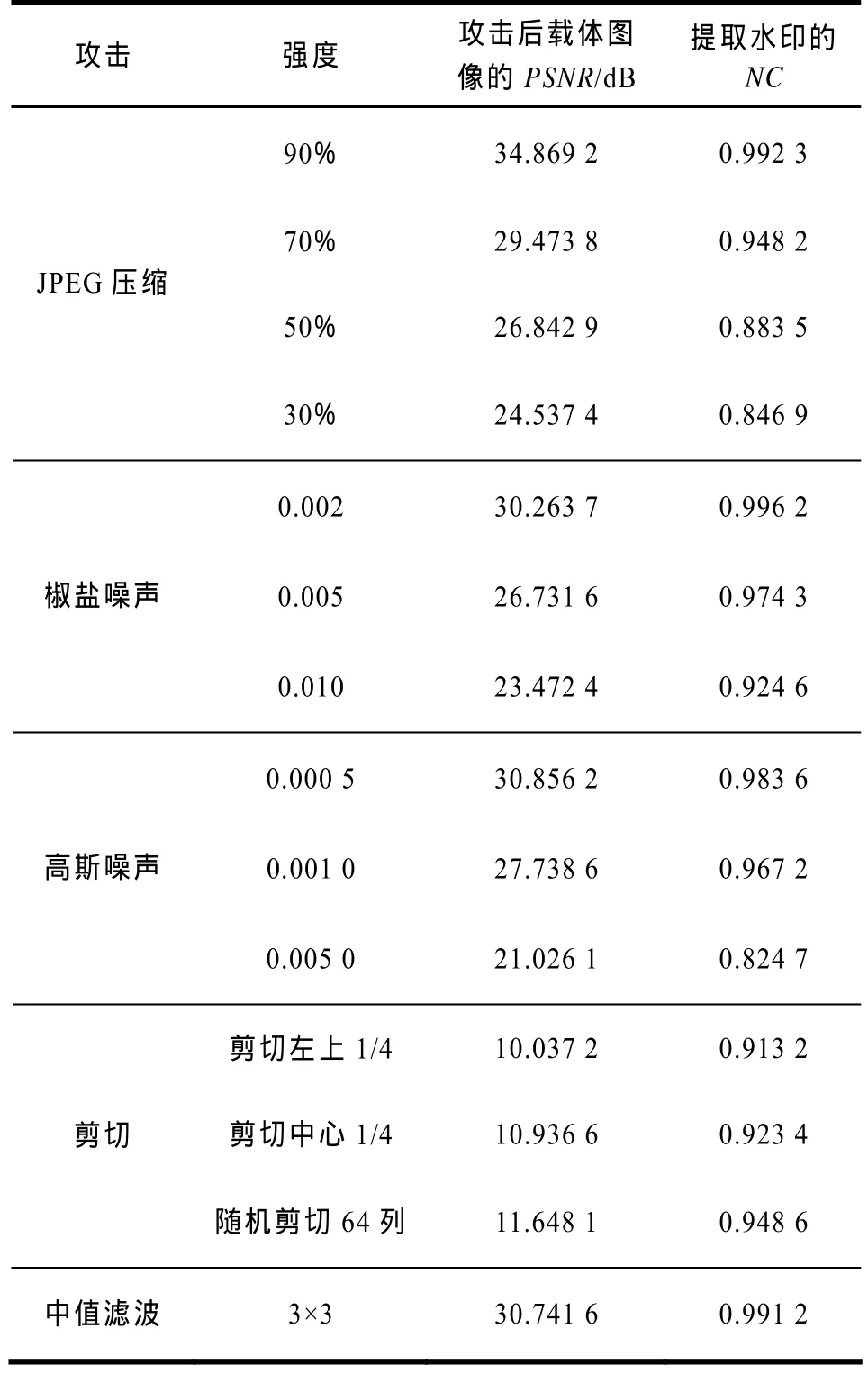
表1 提取水印实验结果

6 结束语

本文提出一种基于离散四元数傅里叶变换的双彩色图像数字水印算法。首先对彩色宿主图像和水印图像分别进行离散四元数傅里叶变换得到其频谱，然后利用3个互不相关的混沌序列分别对水印频域进行置乱，最后通过选择适当的频域系数，实现彩色水印图像的嵌入。实验结果证明，该算法在保证水印透明性的同时，具有较强的鲁棒性。另外，提取算法的版权水印时不需要原始载体图像，因此，属于盲水印技术。

[1]王向阳, 杨红颖, 赵 红, 等.自适应小波域数字水印嵌入算法研究[J].小型微型计算机系统, 2006, 27(7): 1353-1357.

[2]石红芹, 吕方亮, 刘遵雄.基于混沌加密的彩色图像盲数字水印算法[J].计算机工程, 2011, 37(20): 105-107.

[3]Ahmidi N, Safabakhsh R.A Novel DCT-based Approach for Secure Color Image Watermarking[C]//Proc.of International Conference on Information Technology:Coding and Computing.Hyderabad, India: [s.n.], 2004.

[4]孙 锐, 孙 洪, 姚天任.多通道的小波域彩色图像水印算法[J].计算机辅助设计与图形学学报, 2003, 15(8):992-997.

[5]Nikolaidis N, Pitas I.Robust Image Watermarking in the Spatial Domain[J].Signal Processing, 1998, 66(3): 385- 403.

[6]胡裕峰, 朱善安.基于双混沌置乱和扩频调制的彩色图像盲水印算法[J].光学学报, 2008, 28(9): 1691-1696.

[7]Jin Lianghai, Li Dehua.An Efficient Color Impulse Detector and Its Application to Color Images[J].IEEE Signal Processing Letters, 2007, 14(6): 397-400.

[8]Baraniuk R B, Chan W L, Choi H.Coherent Multi-scale Image Processing Using Dual-tree Quaternion Wavelets[J].IEEE Translations on Image Processing, 2008, 17(7): 1069-1082.

[9]Ell T A.Hypercomplex Color Affine Filters[C]//Proc.of IEEE International Conference on Image Processing.San Antonio, USA: IEEE Press, 2007: 249-252.

[10]Bas P, le Bihan N, Chassery J.Color Image Watermarking Using Quaternion Fourier Transform[C]//Proc.of IEEE International Conference on Acoustics, Speech, and Signal Processing.Hong Kong, China: [s.n.], 2003: 521-524.

[11]孙 菁, 杨静宇, 傅德胜.彩色图像四元数频域幅值调制水印算法[J].计算机科学, 2011, 38(3): 123-126.

[12]Ell T A, Sangwine S J.Hypercomplex Fourier Transforms of Color Images[J].IEEE Transactions on Image Processing, 2007, 16(1): 22-35.