三次B样条曲线插补技术修正算法*
2013-09-29张万军胡赤兵邬再新张国华王保民
张万军 胡赤兵 邬再新 张 峰 张国华 王保民
(①兰州工业化设备有限公司,甘肃兰州730050;②兰州理工大学机电工程学院,甘肃兰州730050;③兰州理工大学数字制造技术与应用省部共建教育部重点实验室,甘肃兰州730050)
对于曲面处理而言,NURBS是目前流行的自由曲线与自由曲面的表达式,但其生成原理和表达式相对较为复杂。B样条计算量大,特别是非均匀有理B样条(NURBS),将严重影响运动的响应时间。为了减少计算量,主要研究三次均匀有理B样条曲线。而三次B样条曲线由于能够满足处理一般工程问题的需要(当特征点或型值点之间的距离比为1/3~3时,其与三次NURBS曲线的差异很小)且计算简便[1],因此三次B样条曲线是工程上广泛采用的曲线构造方法和工程技术人员解决相关问题的首选。
对于三次B样条曲线插补算法的研究已有大量的文献,其中许多算法都是为了力求在计算机上快速产生曲线而设计的,三次B样条曲线大多数采用解三角方程组的方法,如递推耦合法、循环约化法、矩阵分解法的并行算法,但对于多核计算机来说不一定都适用[2]。姚哲[3]提出一种基于泰勒公式的用于实时控制的任意空间参数曲线插补方法,叶伯生[4]提出NURBS曲线曲面得到广泛应用。这些文献都是关于NURBS曲线曲面插补参数递推的插补,泰勒展开式一阶、二阶求解比较复杂,加工误差较大。本文主要针对三次B样条曲线的表达式泰勒公式展开式一阶、二阶展开式,修正调节插补增量Δu与插补速度v的关系,以达到修正改进原三次B样条曲线插补的目的。Δu与插补速度经实例验证表明该插补算法可以提高插补运算效率,大大地节约计算时间,从而实现样条曲线的快速插补。
1 三次B样条曲线的数学定义
近年来,以 NURBS(Non-Uniform Rational BSpline非均匀有理B样条)为内部描述的自由曲线曲面造型技术得到广泛的应用和发展。NURBS不仅能精确统一地表示标准解析曲线和自由曲线,而且它的控制能力也是十分强大、灵活的。鉴于此原因,国际标准化组织(ISO)将NURBS方法定为STEP中的唯一数学方法。
NURBS曲线一分段的矢值有理多项式函数,其表达式为[5]
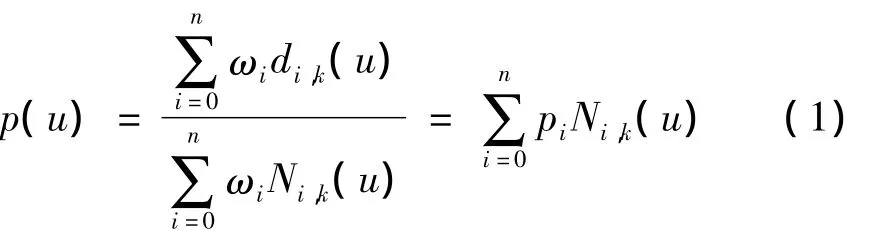
式中:di(i=0,1,…,n)为控制点,又称德尔布点,每个控制点对应一个相应权的权因子ωi。U=[u0,u1,…,un+k+1]称为节点矢量,Ni,k(u)为k次规范B样条基函数(对于本文涉及的三次NURBS曲线,k=3),是关于节点矢量的函数,其递推公式中ωi为权因子(i=0,1…,n),di,k(u)分别控制顶点相联系(i=0,1…,n),Ni,k(u)为k次样条基函数。按 Cox-de Boor递推公式确定的k次规范B样条基函数,可由下式递推计算[3]:
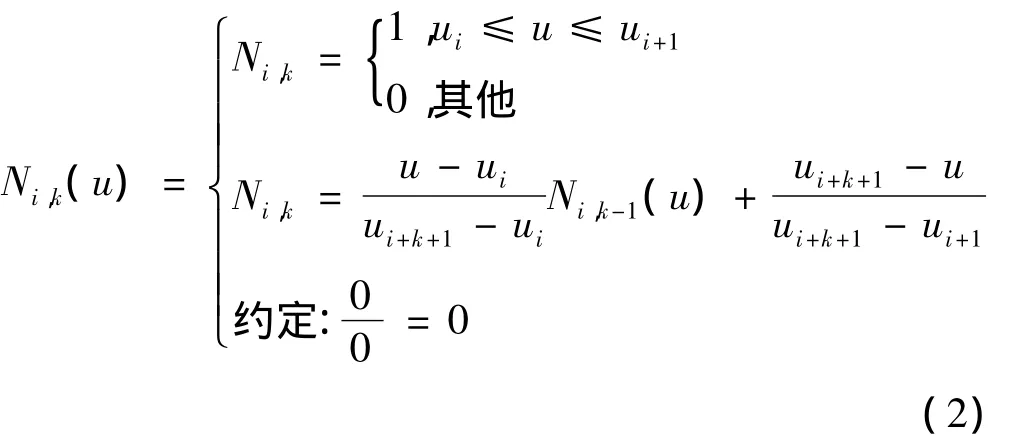
式中,ui是节点值,且为非减序列,U=|u0,u1,…,un+k+1|构成了k次(k+1)B样条基函数的节点矢量,每一基函数由对应的k+2个节点确定。式(2)表明,高次B样条曲线可用低次B样条函数来表示,由此递推且节点数目由控制顶点di(i=0,1,…,n)和曲线次数k确定(节点数目是m=n+k+2,n为控制项的点数,k为B 样条基函数的阶数)[6]。
在式(2)中B样条曲线的方程式令k=3时,将式(1)改写为
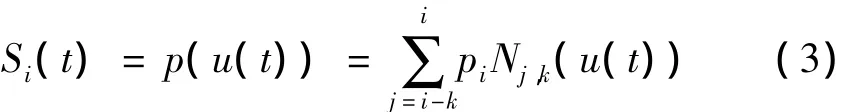
将式(3)写成矩阵的形式:

其中1 ~3 次系数矩阵Nk(k=1,2,3;i=0,1,2,3)分别为:
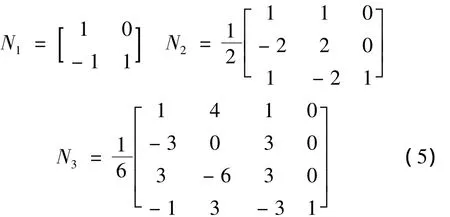
这样,式(2)不用递推即可展开,即可得到上述矩阵形式(二次均匀B样条曲线):
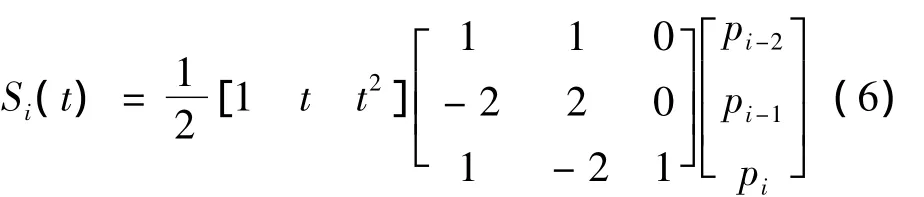
同理可得到三次B样条曲线的方程形式:

2 三次B样条曲线修正的算法
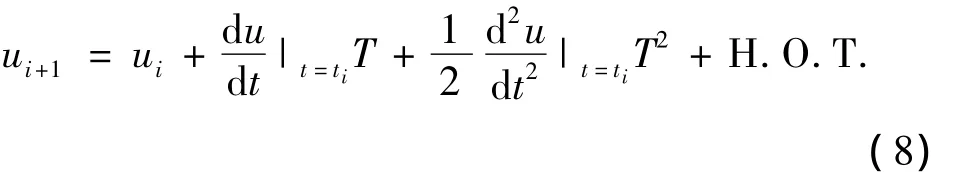
式中:H.O.T.是指 Taylor展开的高阶项(High Order Terms)。
2.1 泰勒公式一阶展开式的近似计算
设v为沿曲线的进给速度,可由曲线对时间t求导得到[6-9]:
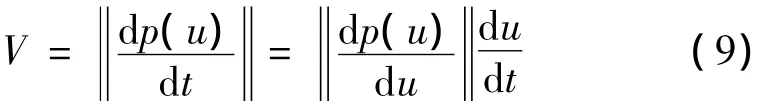
本算法针对三次B样条曲线参数的插补,采用快速递推的近似算法来预估新插补点的参数时,发现泰勒公式展开式的一阶导数、二阶导数在每个插补周期T内有相等的微小增量Δu,参数增量周期T恒定,Δu与插补速度v有关,因此本文提出三次B样条曲线修正插补算法。根据泰勒公式展开式(二阶展开式)得:
因此,u对t的一阶导数可以表示为

将式(9)、(10)代入式(8)得到泰勒公式一阶展开式的近似计算公式为
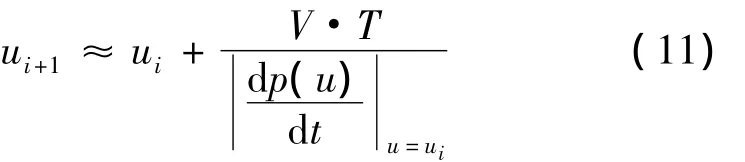
当插补周期T→0时,ui+1≈ui,可以满足泰勒公式一阶展开式插补近似迭代。
2.2 泰勒公式二阶展开式的近似计算
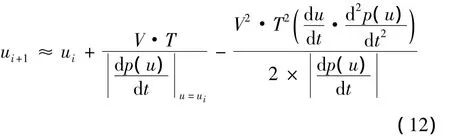
进一步求导可以得u对t的二阶导数:
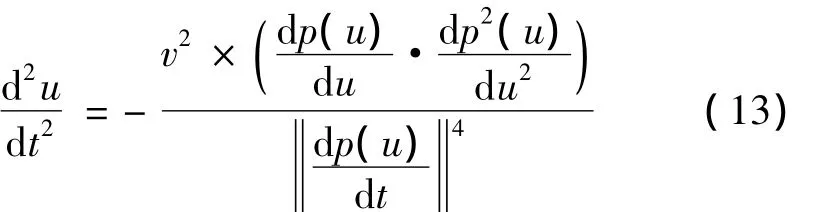
设NURBS B曲线表示为p(u),则该曲线上参数u=ui的曲率为

所以该点曲率半径Ri为

当Ri→∞,即k→0时,则有:
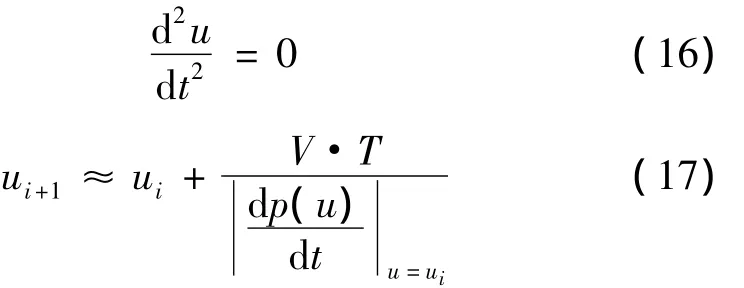
如果曲线曲率半径很小,便可以满足泰勒公式二阶展开式插补近似迭代[10]

由式(11)、(18)可知,插补增量Δu由进给速度V和插补周期T决定,在每一个插补周期中弦长不变,则插补周期是不变的。
3 插补算法流程图
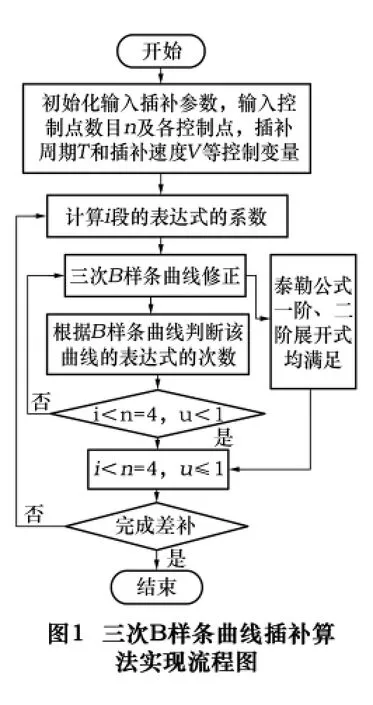
在NURBS曲线时间分割插补的过程中,首先设置插补条件以及初始化参数,通过循环计算每一步的参数值,得到新的数据点,从而实现插补。同时,在插补的过程中要使弓高误差保持在一定范围内,保证插补进度实现插补运算[11]。要使上面的插补算法实现,具体的插补算法的流程图如图1所示。
4 算法实例及分析
4.1 插补算法实例
任意输入一组三次B样条曲线的参数,在数控机床中实现插补。例如由参数U=[0 0 0 0 0.45 0.636 0.742 1]控制顶点d0(0,0,1),d1(25,30,6),d2(50,50,16),d3(65,60,22),d4(77,70,30),相应权因子ω=[1.6 1.7 0.7 1.25 0.6 0.85 1 1.2 1.2]
调用仿真程序,读取NURBS插补G代码G06.2,NURBS.txt',rt'在数控机床中完成插补。

对此自由NURBS曲线进行实时动态轨迹仿真插补,其最后结果如图2所示。
4.2 插补算法分析
根据前面文章中给出的任意点三次B样条曲线插补参数,做出原曲线与修正曲线的轮廓误差图如图3所示。
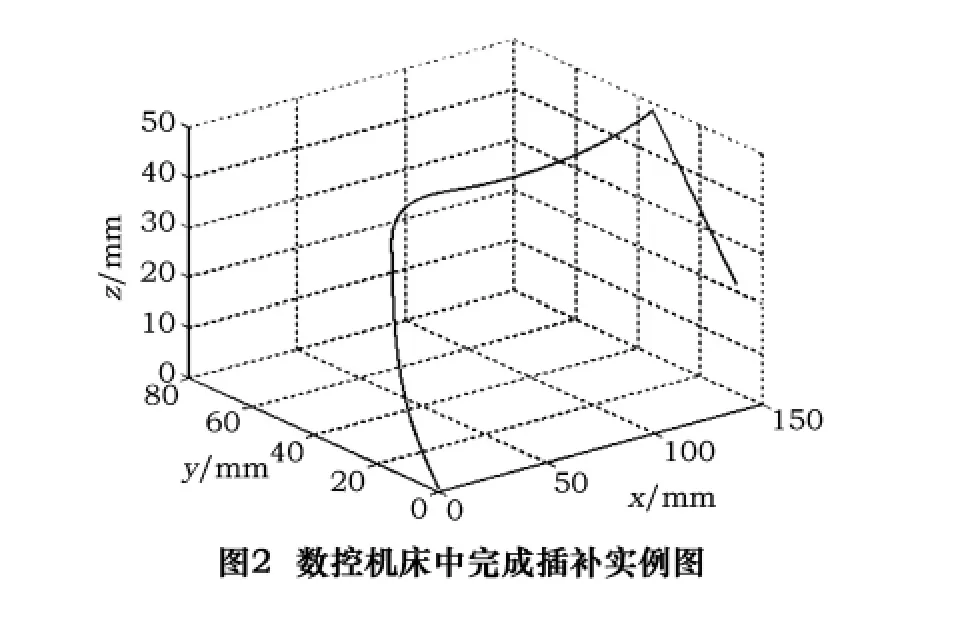

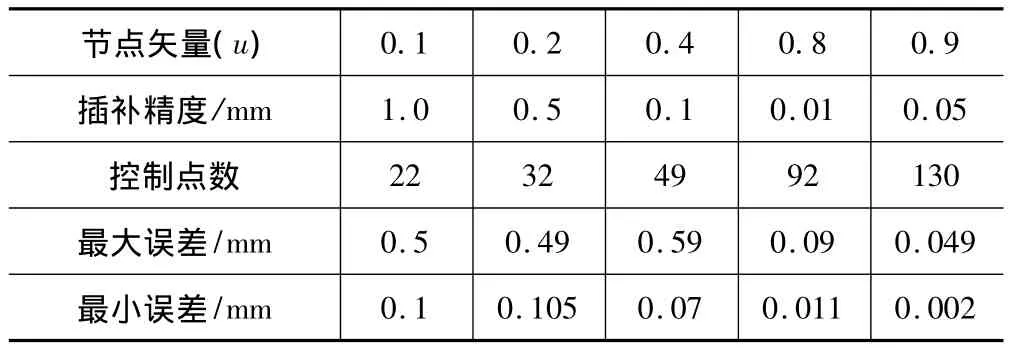
表1 修正后的曲线与原曲线精度误差分析
从图3可以看出,修正后的三次B样条曲线实现了快速插补运算。减小了轮廓误差,但仍需要对新修正的插补算法与原插补算法做如表1所示的精度误差分析。
由表1可知,该插补算法减小了插补误差,提高了插补精度,节约了插补时间,同时也提高插补运算的效率,满足插补的要求。
5 结语
(1)分析了三次B样条的泰勒公式一阶、二阶展开式在插补周期一定的情况下,插补增量只与插补速度有关,通过改变插补增量可以达到插补修正的目的。并结合具体实例在MATLAB 7.0上验证该算法是正确的,达到了参数修正的目的。
(2)该插补算法简化了三次B样条曲线数学递推公式推导的过程,实现样条曲线的快速插补,对应用该插补算法解决三次B样条曲线等重大的工程问题具有重要的现实意义。
[1]方忆湘,刘文学.基于几何特性的三次均匀B样条曲线构造描述[J].工程图学学报,2006(2):96 -102.
[2]苗莎,郑晓嶶.三次插值样条曲线拟合多核并行算法[J].计算机应用,2010,12(30):3194 -3196.
[3]姚哲,冯景春,王宇晗.面向五轴加工的双NURBS曲线插补算法[J].上海交通大学学报,2008,42(2):2 -8.
[4]叶伯生,杨叔子.CNC系统中三次B样条曲线的高速插补方法研究[J].中国机械工程,1998,9(3):42 -43.
[5]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京:高等教育出版社,2001.
[6]田国华,黄德超,欧长劲.多管相贯坡口曲线数控切割割炬姿势态控制函数的重构[J].兰州理工大学学报,2011,37(5):46 -49.
[7]Cox M G,Cheng M Y.The numerical evaluation of B - spline[J].J inst Maths Applications,1972(10):134 -149.
[8]邬再新,张万军,胡赤兵,等.NURBS修正插补算法的研究[J].制造业自动化,2011,11(33):48 -50.
[9]张万军.复杂曲线曲面插补技术修正算法的研究法[D].兰州:兰州理工大学,2011.
[10]孔凡国,郝尚华,钟延志.三次 B样条曲线插补算法的VC实现[J].中国新技术新产品,2009(17):8 -9.
[11]Tasi Meng-Shium,Nien Hao-Wei,Yau Hong-Tzong.Development of an integrat- ed look-ahead dynamics-bases NURBS interpolator for high presion machining[J].Computer Aided Design,2008,40:554-556.
