基于灰色理论的水泥路面拉杆传荷能力有限元分析

徐真真,曹高尚,王 杰

（1.天津市市政工程设计研究院，天津市 300051；2.长安大学，陕西西安 710064）

0 引言

水泥混凝土路面通过设置接缝来解决温度、湿度变化所引起的路面不均匀开裂。为了保证水泥路面结构的整体性，通过在纵缝处设置一定数量的拉杆来防止因温度升高时板体向两侧移动[1]。我国的水泥路面设计方法中针对拉杆的设计主要考虑在温度收缩作用下拉杆本身的抗拉强度及拉杆与水泥混凝土之间的粘结力是否超过容许拉应力，并没有考虑拉杆的实际受荷特性及其传荷性能；周德云等曾对不同路面结构刚度、荷载形式以及路面板尺寸条件下纵缝处挠度比与应力折减系数之间的关系进行了回归分析，并将其计算结果应用于有接缝旧水泥路面的传荷能力评价和新建水泥路面的接缝设计[2]；张军等采用双参数地基并考虑层间接触对拉杆传荷性能进行了分析，其结果认为纵缝处设置拉杆后板底拉应力较未设置拉杆最大拉应力减少了22.8%，弯沉值下降了13.9%[3～5]。而在实际工作状态下，拉杆同传力杆同样存在初始松动，该松动的存在对于拉杆的传荷性能影响以及拉杆处荷载传递的正确表征却鲜见报道。

笔者采用三维有限元方法，结合Winkler地基模型并考虑拉杆处混凝土不同初始松动量，对实际工况下拉杆应力分布及纵缝处荷载传递能力进行了分析计算，得到了存在初始松动条件下拉杆的传荷性能表征，并采用灰色关联度理论分析了不同松动因素对拉杆传荷性能的影响大小，为水泥路面拉杆传荷性能评价及其定量评价指标研究奠定了理论基础。

1 三维有限元模型建立

计算中将地基简化为Winkler模型，地基模量取200 MPa/m，水泥混凝土路面板取为弹性薄板，几何尺寸为“长×宽×厚=5 m×3.5 m×0.26 m”，接缝宽度为1 cm，拉杆长度为45 cm，直径为14 mm，根据实际路面尺寸简化后最终确定的各结构几何尺寸及计算参数见表1。

表1 各结构计算参数

荷载采用规范荷载作用方式BZZ-100，根据研究当轮胎处于标准胎压0.7 MPa时接地轮胎截面趋向于矩形，因此为了更好地模拟轮胎接地压力的实际情况，选择标准轴载情况下的矩形接地面积，每个轮胎接地几何尺寸为20 cm×20 cm，双轮组间距为20 cm，荷载作用于路面板横向中间纵向接缝处边缘，见图1。

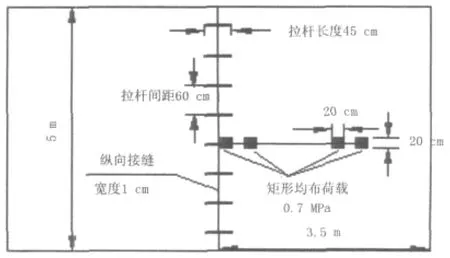
图1 纵缝处路面板荷载作用方式图

建立三维模型后在拉杆钢筋靠近接缝处植入“楔形”松动，接缝处松动量最大，逐渐向两侧递减，松动植入位置按照图2所示进行，其中松动厚度分别取0.1 mm、0.3 mm、0.5 mm，松动长度取2 cm、4 cm、6 cm、22 cm（全部松动），具体见图 2。

图2 松动植入位置图

2 不同工况下拉杆传荷性能对比

2.1 拉杆传荷能力评价指标

根据以上方法计算得到的水泥路面处植入松动后纵缝附近应力分布及拉杆横断面应力分布分别见图3、图4。

图3 拉杆处纵断面应力分布图

图4 拉杆横断面应力分布图

拉杆传荷能力计算采用两种方法进行比较，定义应力传导率以拉杆底部混凝土松动尖端应力比值百分率为表征：f=，σ-未受荷板混凝土松σ1动尖端应力（MPa），σ2-受荷板混凝土松动尖端应力（MPa）；定义变形传导率以纵缝左右两块板边缘竖向位移的比值百分率为表征：f=，U-未受荷U1板竖向位移（mm），U2-受荷板竖向位移（mm）。为此分别提取得到拉杆底部混凝土表面应力典型分布及纵缝处水泥板顶部竖向位移典型分布见图5、图6。

图5 拉杆底部混凝土应力分布图

图6 接缝顶部水泥板竖向位移图

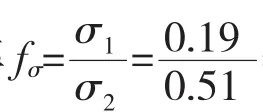
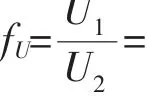
2.2 计算结果分析

根据以上方法分别计算得到不用工况下设拉杆水泥路面纵缝处应力传导率及变形传导率见表2、表 3 及图 7、图 8。

表2 不同工况下设拉杆水泥路面纵缝处应力传导率（%）

表3 不同工况下设拉杆水泥路面纵缝处变形传导率（%）

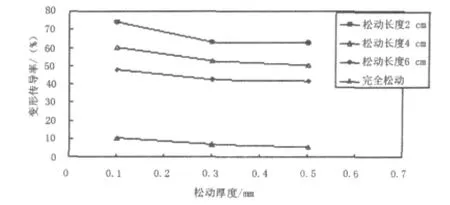
图7 不同工况下设拉杆水泥路面纵缝处应力传导率

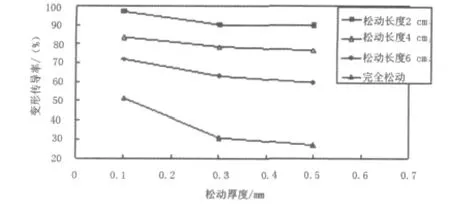
图8 不同工况下设拉杆水泥路面纵缝处变形传导率

结合图7、图8对表2、表3中的数据做如下分析：相同工况条件下，应力传导率较变形传导率低20%～30%，随工况变化，二者变化趋势相同，表明用两种不同方式表示的传导率较符合；松动长度每增加2 cm，应力传导率降低约10%，全部松动时，应力传导率降至10%以内，应力传到效果差；随松动厚度增加，应力传导率逐渐降低，0.3 mm处出现拐点，应力传导率渐趋稳定。

工况因素影响程度分析：

为确定松动厚度及松动长度对设拉杆水泥路面纵缝处荷载传递的影响大小，根据灰色理论对松动厚度及松动长度影响应力传到率大小进行分析[7][8]，计算过程及结果见表4～表7。

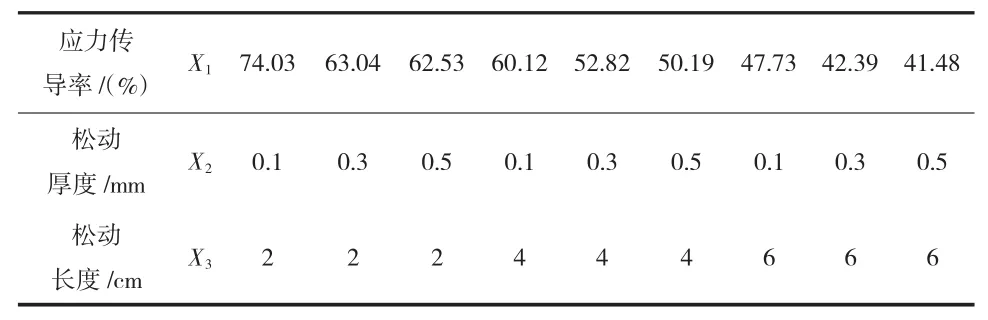
表4 应力传导率及松动因素

表5 初值像

表6 差序列

表7 关联系数

对表7中关联系数求和得到Σγ12=5.29＜Σγ13=6.23，松动厚度对传荷系数影响小于松动长度对传荷系数的影响。

2.3 不同传导率相关性分析

对表2及表3中应力传导率及变形传导率进行回归分析，回归结果见图9。

图9 传导率回归分析

由图9可得如下结论：应力传导率与变形传导率有较高的相关性，二者呈线性关系，实际工程应用中可在实际工况条件下采用变形传导率估计应力传导率，进而得到松动尖端的应力比水平，为纵缝拉杆工作性能做进一步评估。

3 结语

（1）考虑不同工况条件下水泥路面接缝处两种不同的荷载传导效率变化可知：相同工况下，应力传导率与变形传导率变化趋势相同，二者较为符合；随松动量的增加，拉杆传荷能力降低。

（2）根据灰色理论得到松动长度与传导率的关联系数为松动厚度与传导率的关联系数的1.2倍，松动长度对拉杆传荷能力影响大于松动厚度对拉杆传荷能力影响。

（3）回归分析应力传导率与变形传导率，二者具有较高的线性相关关系，可采用变形传导率用以反算应力传导率用以评价实际工况下拉杆工作性能。

[1]Chou Yu T.Structural analysis computer programs for rigid multicomponent pavement structures with discontinuities-WESLIQID and WESLAYER[R].Technical Report GL-81-6,Washington,D.C,181,9-40.

[2]周德云,姚祖康.水泥混凝土路面接缝传荷能力的分析.上海:同济大学学报[J].1993,12(1):58-65.

[3]张怀志.普通水泥路面传力杆及拉杆研究[D].哈尔滨工业大学,2007:26-40.

[4]张军,李剑波,边惠英.刚性路面缩缝传力杆的受力分析与设计[J].中南公路工程学报,2001,26(4):7-8.

[5]王岩,石志飞.钢筋与混凝土界面的疲劳裂纹扩展研究[A].第十届全国疲劳与断裂学术会议论文集[C].2000.

[6]刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京:科学出版社,2004.

[7]李学全,李松仁,韩旭里.灰色系统理论研究(Ⅰ):灰色关联度[J].系统工程理论与实践,1996,(11):91-95.