立式加工中心热态有限元分析与实验研究*
2013-09-28祝莉平张建富郁鼎文
祝莉平 陈 玉 张建富 郁鼎文
(①南通科技投资集团有限公司,江苏南通 226000;②清华大学机械工程系,北京 100084)
在机床工作过程中各部位热源产生的热量传给机床各部位,温升导致相应零部件发生热变形,并使机床在加工过程中工件与刀具之间相对位移发生变化,从而影响加工精度[1]。在精密加工中,由热变形引起的精度损失高达总精度损失的40% ~70%[2]。
天津大学李书和等[3]分析了影响机床温度场因素,在切削热较小的情况下,机床主轴附近的温度场主要受主轴转速的影响,而环境温度和其他因素对其影响较小。主轴系统中,最主要的两大热源是轴承摩擦产生的热以及电动机带来的热量[4]。有限元法分析机床热态已成为主流方法,准确的有限元分析模型除了需要准确定义机床的发热和散热条件外,结合面热阻的定义也是关键之一。结合面热阻是互相接触的介质之间的热传递的重要参数之一,在机床热态分析中对机床温度分布有重要影响。
本文以南通科技投资有限公司生产的VCL1100立式加工中心为例,对其热态有限元分析与实验进行了研究。在全面分析机床空转时发热和散热条件及结合面热阻的情况下,建立整机热态有限元分析模型,对其温度场分布和热变形进行了仿真分析,并与实验获取的结果进行比较和分析。仿真和测试结果对该加工中心的优化设计提供了理论和实验基础。
1 机床热态有限元建模与分析
1.1 机床热态有限元建模
机床热态性能有限元分析模型需要包括(如图1):机床结构有限元模型、机床热属性(零部件材料和结合面热属性)、热态边界条件(发热和散热条件)。在机床空转时,发热源主要包括电动机发热和主轴轴承发热,散热主要包括冷却系统的强制冷却和空气对流及热辐射换热。在已知的边界条件下,立式加工中心的温度变化及热变形是由材料的比热、密度、导热系数、弹性模量及线胀系数等热物性参数决定的。立式加工中心的各零部件的材料主要有20Cr、45#钢和HT300这3大类,外部环境为自然对流的空气,材料各项热物性参数取手册中数据的定常平均值。
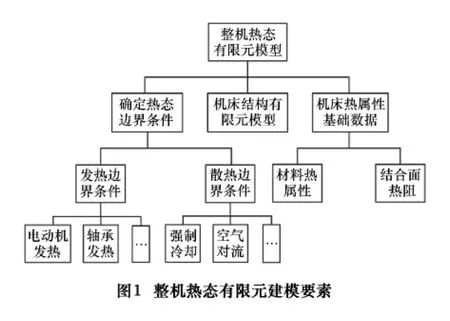
该立式加工中心采用FANUC公司αiI 8/8000型号的主轴电动机,额定功率7.5 kW,电动机发热传递到主轴箱体的发热功率约为30 W。主轴支撑单元采用NSK角接触球轴承7014CTYNDBBLP4。没有对主轴组件内部通冷却油,而在其主轴箱体前部和两侧开有冷却槽,通入循环冷却液对主轴箱进行冷却。根据相应的经验公式,估算有限元分析模型所需的主轴轴承发热功率、机床旋转体对流换热系数、表面和周围空气之间传热系数[5-6]。
整机热态仿真分析时,为了获得可靠的计算数据,需考虑结合面热阻的影响。在ANSYS软件热态仿真环境中,结合面的属性有Thermal Conductance选项,它的大小就是结合面热阻的倒数,可以通过设定该选项的值来添加结合面处的热阻。

表1 模型中主要结合面采用的热阻表
本研究考虑对机床传热及变形影响较大的主要结合面处的热阻,如主轴轴承内、外圈与主轴、轴套结合面的热阻,轴套与主轴箱结合面的热阻,主轴箱与立柱结合面的热阻,标准测试棒与锥套结合面的热阻。根据结合面两侧零部件的材料属性及表面形貌,接触介质和压强,代入清华大学结合面热阻数据库,可以获得立式加工中心关键结合面处的热阻如表1所示。
为了便于有限元分析,对整机结构进行必要的简化。如图2所示为划分网格后的有限元模型,总共划分227 127个单元和409 884个节点。
1.2 仿真分析结果
利用以上热态分析模型,可获得不同转速时整机温度场和热变形。当主轴转速设定为4 000 r/min时,设定立式加工中心的整机初始温度为25.4℃,瞬态热仿真的时间设定为23 400 s。整机热态性能仿真结果如图3所示。

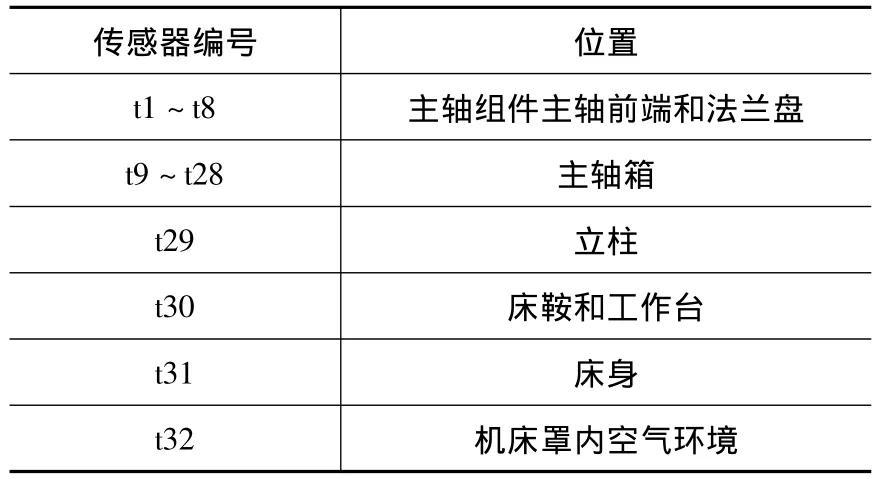
表2 温度传感器的编号及位置分布

表3 温度场有限元实验仿真结果对比表
2 机床热态测量实验设计
2.1 温度传感器的布置
主轴空转时,机床主要热源分布在主轴区域和主轴箱附近。结合实际测量时的空间限制,32套PT100铂电阻温度传感器的布置如表2所示。图4给出了温度传感器t9~t28在VCL1100主轴箱的安装位置。
2.2 位移传感器的布置
将BT40主轴精度检测棒安装到VCL1100机床上,用optoNCDT1700型和LK-031型CCD激光位移传感器分别测量BT40主轴精度检测棒轴心位置沿机床X、Y方向相对工作台的热变形位移量,用EX-305V型涡电流位移传感器测量BT40主轴精度检测棒底端相对工作台的热变形位移量。位移传感器的布置如图5所示。

3 结果对比与分析
3.1 温度场对比
通过2.1节介绍的实验方案,获取机床关键点温度,与VCL1100立式加工中心温度场的有限元仿真结果进行对比。分别取主轴法兰上的编号为t7的传感器、主轴箱前端面主轴轴承处的编号为t11的传感器、主轴箱上端打刀缸处的编号为t20的传感器和主轴箱侧面靠近电动机端的冷却槽处的编号为t24的传感器的仿真温升与实验温升值进行比较,如表3所示。可见,各转速下的仿真值与实验值误差在10%以内,温度场仿真结果可信度较高。
3.2 热变形有限元仿真与实验结果对比
通过2.2节介绍的实验方案,获取主轴验棒的三向位移量,与VCL1100立式加工中心的热变形的有限元仿真结果进行对比,如表4所示。可见,沿Y和Z方向,各转速下的仿真值与实验值误差在10%以内,仿真结果准确性高。
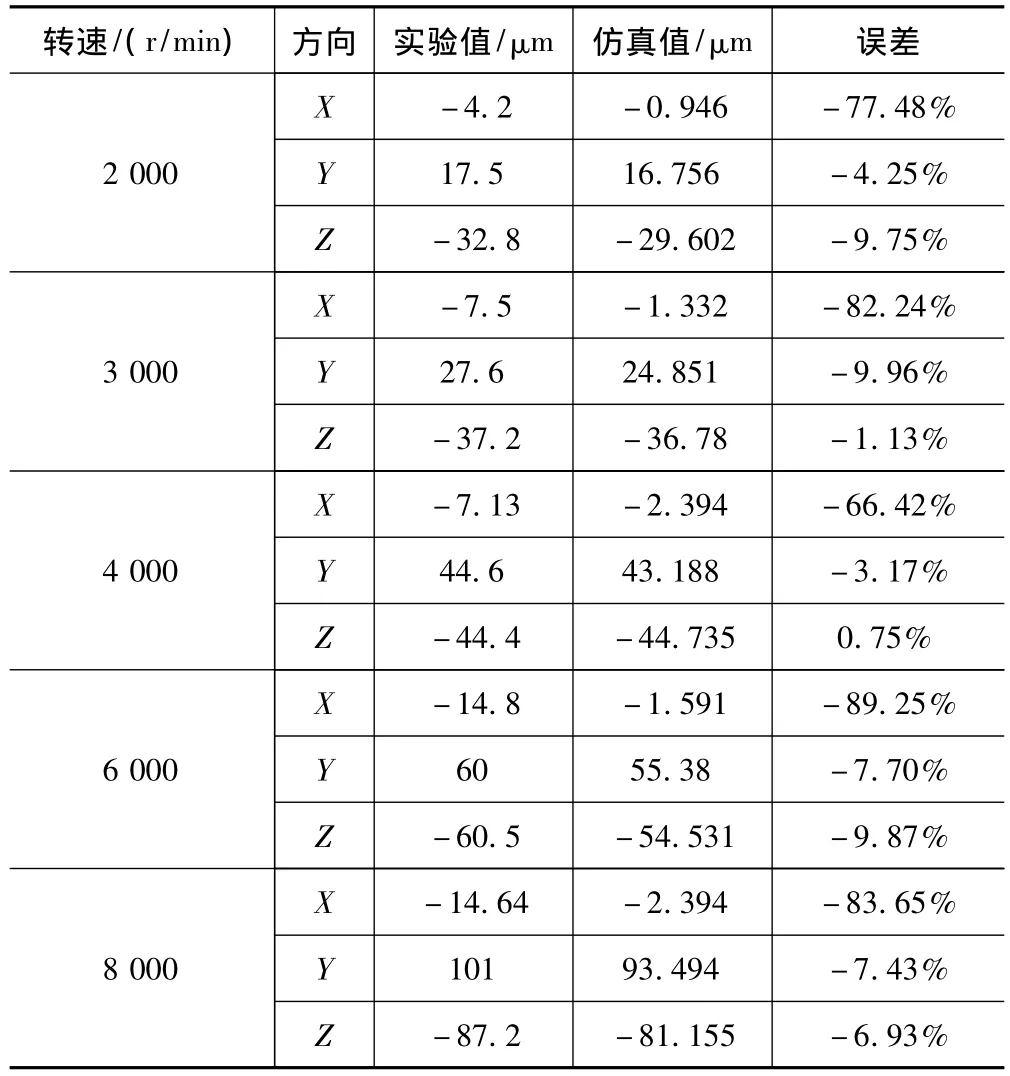
表4 热变形有限元仿真与实验结果对比表
沿X方向的各转速下的仿真误差较大,因为该结构形式的机床沿X向为高度对称结构,仿真模型中的热源和热边界条件也是沿X向对称分布,不考虑其他机构引入的热及结构的复杂性,单纯由主轴发热引起的X向变形很小,实测出其热变形值也很小,因此较小的仿真绝对误差会导致相对误差特别大。实际上,X方向热变形量远小于其他两个方向,对机床加工精度的影响不大,因此这里在对机床热态性能的评价时,主要依据机床在Y向和Z向实验值与仿真值。
4 结语
本文研究了立式加工中心的热态性能仿真技术,通过建立VCL1100立式加工中心的有限元仿真模型,对ANSYS热-结构耦合仿真所需的边界条件进行了分析,在考虑结合面热阻的情况下,对VCL1100立式加工中心在不同转速下的整机热态性能进行仿真分析,并与实验测量的结果进行对比验证。
(1)整机温度场和整机沿Y、Z方向的热变形仿真结果与实验测量结果的误差基本在10%以内。
(2)整机热变形沿X方向的仿真误差较大。考虑到VCL1100结构对X方向而言就较好的热对称性,发热导致的主轴X向热变形绝对值很小,较小的绝对误差就会导致相对误差较大。因此对该结构性形式的机床热态性能仿真效果进行评价时,应主要依据机床在Y向和Z向的热变形结果。
(3)基于以上两点,本文所建立的热态分析有限元模型可靠性较高,能够为进一步的热态性能优化提供了仿真依据。
[1]王金生.XK717数控机床热特性研究[D].浙江:浙江工业大学,2004.
[2]Bryab J.International status of thermal error research[J].Annals of CIRP,1990,39(2):645 -656.
[3]Li S H,Zhang Y Q,Zhang G X.A study of pre-compensation for thermal errors of NC machine tools[J].International Journal of Machine Tools and Manufacture,1997,37(12):1715 -1719.
[4]曹骏.HTM850G数控加工中心主轴系统的热特性研究[D].浙江:浙江大学,2007.
[5]Chen T y,Wei W J,Tsai J C.Optimum design of headstocks of precision lathes[J].International Journal of Machine Tools & Manufacture,1999(39):1961-1977.
[6]周芝庭,冯建芬.基于ANSYS的加工中心机床热特性有限元分析[J].机械制造与研究,2008,37(6):22 -24.
