力电冲击荷载下PZT／复合材料梁界面断裂分析

白 瑞 祥＊， 王 亮， 陈 浩 然

（大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024）

0 引 言

压电材料在航空航天、汽车和电子工程等领域得到了越来越多的应用，如PZT系列压电陶瓷.由于压电材料经常粘贴在基体表面，在制造或使用过程中形成的界面裂纹是压电智能结构最常见的失效模式之一.很多学者对压电材料界面静态断裂行为进行了研究［1－2］.压电材料在航空航天、电子封装等领域的应用中经常受到各种冲击荷载，因此，界面裂纹的动态断裂行为是一个很重要的现象，不能忽视.目前已有一些学者对压电材料的动态断裂进行了研究.Ueda通过Laplace和Fourier转换方法，对含有中心裂纹的压电材料和压电层合结构在法向冲击荷载作用下的断裂问题进行了研究［3］.Shina等通过积分转换方法，对功能梯度压电材料界面裂纹动态扩展问题进行了研究［4］.Zhao对含界面裂纹的压电层合板进行了传导分析，得到了随时间变化的应力强度因子和电位移强度因子［5］.Hu等通过动态J－积分分析了压电双材料界面裂纹在力电冲击荷载作用下的能量释放率［6］.Jin等建立了脱胶的压电／胶层／基体的一维解析模型，对在高频电荷载作用下界面裂纹的应力分布进行了研究［7］.但是，目前对PZT／复合材料界面裂纹在力电耦合冲击荷载作用下的研究还较为有限.

本文基于非线性有限元分析和虚裂纹闭合技术，并采用接触单元防止PZT片和复合材料板分层前缘发生穿透现象，对含有界面裂纹的PZT／复合材料梁在力电耦合冲击荷载作用下的能量释放率进行分析，讨论压电效应、电压和铺层角度对冲击荷载的影响，同时讨论界面接触对结果的影响.

1 基本理论

1.1 虚裂纹闭合技术

虚裂纹闭合技术最早由Irwin提出［8］，图1为虚裂纹闭合技术3D有限元分析示意图.其基本概念是假设长度为a的裂纹，其尖端扩展微小长度Δa时所释放的能量等于将其闭合时所需要做的功［9］.

GⅠ、GⅡ、GⅢ可用下式表示：其中GⅠ、GⅡ、GⅢ分别为Ⅰ、Ⅱ、Ⅲ型裂纹能量释放率，ΔA＝Δab，在这里ΔA是裂纹尖端处分层的虚拟闭合面积，Δa是分层前缘单元的长度，b是单元宽度.

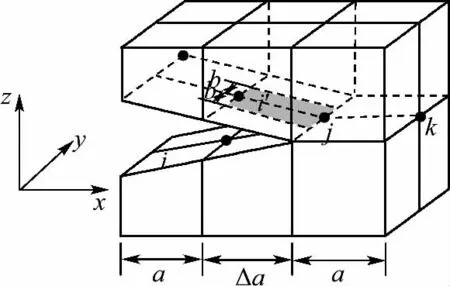
图1 虚裂纹闭合技术3D有限元分析示意图Fig.1 Schematic of VCCT for 3DFE analysis

1.2 动力有限元方程

压电复合材料结构的整体动力有限元方程形式为

式中：Muu、Kuu和KuD分别为质量矩阵、弹性刚度矩阵和压电刚度矩阵；D为电位移向量；Fu是机械荷载矩阵；Cuu为阻尼矩阵；FD是电荷载向量；u为结构位移，是时间t的函数.

如果考虑材料Rayleigh阻尼，则

其中αc为常质量矩阵乘子，βj为材料阻尼.

1.3 接触单元

PZT／复合材料梁在冲击的力电荷载作用下，PZT片会和复合材料发生接触并产生穿透现象，为此需要在接触界面设置接触单元，来控制裂纹前缘穿透现象的发生.在分层前缘设置面对面的接触单元，采用罚函数法求解，不考虑滑动摩擦的影响.罚函数法公式为

式中：fn为法向接触力，K为接触刚度，δ为接触位移.接触单元间的穿透值通过分离的接触体上节点间的距离来计算.

2 数值算例和讨论

本文采用3D－VCCT单元，该单元可以有效减少编程工作和避免不必要的计算，在裂尖的节点对间采用刚度很大的弹簧连接来计算其节点力.裂纹尖端周围的节点则用来提取位移等相关信息，并用来计算裂纹尖端后面的张开位移的扩展量.当某一时刻能量释放率达到材料本身的能量释放率临界值时，裂纹向前扩展.删除裂纹尖端的3D－VCCT单元来模拟裂纹的动态扩展，并在删除单元的同时激活裂纹开裂路径上的接触单元，避免裂纹分层前缘可能出现的相互嵌入.

2.1 算例验证

考虑受冲击荷载作用下含有中心裂纹的压电双材料无限大半平面，其几何材料参数见文献［6］.图2分别给出了通过虚裂纹闭合方法和动态J－积分得到的能量释放率.本文计算结果与文献［6］所得结果相比吻合较好，说明了本文分析方法的有效性.

图2 能量释放率随时间t变化曲线Fig.2 The variation of energy release rate with time t

2.2 PZT／复合材料梁界面冲击断裂分析

两个PZT片对称粘贴在复合材料层合梁上下表面，上面PZT片作为作动器，下面PZT片作为传感器，几何模型如图3所示，其中长L＝50 mm，宽W＝20mm，hp＝0.5mm，hc＝0.75mm，在PZT驱动器和复合材料层合板之间有一个初始裂纹a＝10mm，边界条件为两端固定.PZT片表面受到冲击的均布荷载为σ0＝1kPa，电荷载为电压.采用有限元软件ANSYS11.0进行非线性数值分析计算.有限元网格模型如图4所示，并在裂尖处进行了网格加密.

压电片（PZT－4）弹性常数：c11＝139GPa，c12＝74.3GPa，c22＝113GPa，c33＝25.6GPa；压电应 力 常 数：e21＝ －6.98C／m2，e22＝13.84 C／m2，e15＝13.44C／m2；介电常数：k11＝6.0×10－9F／m，k22＝5.74×10－9F／m；面密度ρ＝7 600kg／m2.复合材料单层板厚度为0.125mm，材料参数：面密度ρ＝1 200kg／m2，E1＝135.7 GPa，E2＝E3＝9GPa，ν12＝ν13＝0.24，ν23＝0.46，G12＝G13＝5.2GPa，G23＝3.4GPa.

图3 PZT／复合材料梁几何模型Fig.3 Configuration model of PZT／composite beam

图4 有限元网格模型Fig.4 FE meshes model

图5 裂纹表面接触和压电效应对G／Gn响应的影响Fig.5 The influence on the response of G／Gnwith crack surface contact and piezoelectricity

为了便于比较，定义量纲一电压为R＝Ve22／Lσ0，压电复合材料梁受到冲击外力σ0＝1 kPa，分别选取R为 －0.56、－0.28、0、0.28和0.56.量纲一能量释放率因子Gn＝1 000σ0πa／c22，量纲一时间因子t＝0时，压电作动器上表面和压电传感器下表面同时施加力电冲击荷载，本文所有讨论的能量释放率为压电复合材料梁脱胶前缘A点的能量释放率的响应曲线.图5分别给出了压电和接触效应对PZT／复合材料梁界面裂纹的量纲一总能量释放率随量纲一时间变化的曲线.可以看出，考虑压电效应时界面裂纹的能量释放率比不考虑压电效应时减小了大约50%，说明压电材料由于特有的压电效应对冲击的外力荷载下界面裂纹的起裂有抑制作用，特别是很高机电耦合系数的压电材料，比如本文中使用的PZT－4.通过比较还可以发现，没有压电效应时接触效应对计算结果影响不是很大，但是有压电效应时，不考虑裂纹前缘接触就会引起较大的误差.接触将会减小界面能量释放率的振荡幅度并且推迟其峰值的出现时间.

图6为不同电压作用下PZT／复合材料梁界面裂纹量纲一总能量释放率随量纲一时间的变化曲线.无论施加正电压还是负电压，都会使界面能量释放率响应曲线的波动幅值增大，其增大的幅度要明显高于减小的幅度，且都随着电压的增加而增大.无论施加正电压还是负电压，都会使界面总能量释放率的峰值变大，从而加剧裂纹的起裂扩展.而且，在相同的量级范围内，负电压对界面能量释放率的影响要高于正电压的影响.因此，在对压电复合材料界面断裂分析时，要考虑电压正、负对界面动态起裂行为的影响.在考虑压电效应时，压电片的变形具有自适应性，对界面裂纹起裂具有一定的抑制作用，而对于具有界面缺陷的压电智能复合材料结构，在对结构进行形状控制时所加的驱动电压会加速裂纹的扩展，使结构出现功能失效，可见，充分保证界面黏接质量是十分必要的.

图6 G／Gn在不同电压下的响应曲线Fig.6 Response curves of G／Gnunder different voltages

图7 和8为不同铺层（非均衡铺层）时量纲一的总能量释放率随量纲一时间变化的响应曲线.当施加负电压时，［306］、［456］铺层和［06］铺层时的响应曲线很接近，而［606］、［906］铺层时的响应曲线要高于［06］铺层.当施加正电压时，［306］和［456］铺层的响应曲线则低于［06］铺层，［606］和［906］铺层的响应曲线和［06］铺层的响应曲线很接近.可以看出，复合材料的弯扭以及拉剪特性对PZT／复合材料梁界面的动态能量释放率影响很大，施加电压的正负则导致非均衡铺层对力电耦合的低能量冲击荷载下的界面断裂行为变得更加复杂.

图7 不同铺层下G／Gn响应曲线（R＝－0.28）Fig.7 Response curves of G／Gnunder different stacking sequences（R ＝ －0.28）

图8 不同铺层下G／Gn响应曲线（R＝0.28）Fig.8 Response curves of G／Gnunder different stacking sequences（R＝0.28）

图9 为不同阻尼下量纲一的总能量释放率随量纲一时间变化的曲线.可以看出，考虑压电材料的阻尼后，阻尼越大，响应曲线震荡幅度越小，曲线越光滑，并且峰值的到达时间延缓.图10为不同阻尼下量纲一的总能量释放率峰值随电压的变化曲线.可以看出，考虑压电材料阻尼会减小压电复合材料梁界面动态能量释放率的峰值，而且施加电压越大，阻尼影响越明显.可以看出，力电耦合冲击荷载下的PZT／复合材料梁界面裂纹的能量释放率和其随时间变化规律是与压电材料的阻尼特性密切相关的，驱动电压越大，裂纹尖端能量聚集越大，考虑压电片阻尼则因考虑了能量的耗散而相应降低了裂纹尖端的能量释放率，而不考虑压电材料的阻尼则会低估压电复合材料结构的抗断裂能力.

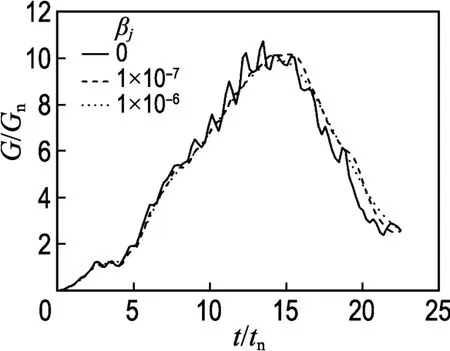
图9 不同阻尼下G／Gn的响应曲线（R＝0.28，αc＝0.01）Fig.9 Response curves of G／Gnunder different dampings（R＝0.28，αc＝0.01）

3 结 论

（1）压电效应对冲击机械力荷载下界面裂纹的动态起裂有很好的抑制作用，特别是高机电耦合系数的压电材料.

（2）不管施加正电压还是负电压，都会加剧PZT／复合材料梁界面裂纹的动态起裂扩展，且铺层角度对界面裂纹的动态能量释放率影响比较复杂.

（3）冲击荷载下一定要考虑裂纹前缘接触行为，另外，不考虑压电材料的阻尼会低估PZT／复合材料结构的抗断裂能力.

［1］Beom H G.Atluri S N.Near－tip fields and intensity factors for interfacial cracks in dissimilar anisotropic piezoelectric media ［J］.International Journal of Fracture，1996，75（2）：163－183.

［2］Narita F，Shindo Y.The interface crack problem for bonded piezoelectric and orthotropic layers under antiplane shear loading［J］.International Journal of Fracture，1999，98（1）：87－101.

［3］Ueda S.Normal impact of a piezoelectric strip with an off－center crack perpendicular to interface ［J］.Theoretical and Applied Fracture Mechanics，2003，39（3）：259－273.

［4］Shina J W，Lee Y S.A moving interface crack between two dissimilar functionally graded piezoelectric layers under electromechanical loading［J］.International Journal of Solids and Structures，2010，47（20）：2706－2713.

［5］ZHAO Xiao－hua.An efficient approach for the numerical inversion of Laplace transform and its application in dynamic fracture analysis of a piezoelectric laminate ［J］.International Journal of Solids and Structures，2004，41（13）：3653－3674.

［6］HU Shu－ling，SHEN Sheng－ping，Nishioka T.Numerical analysis for a crack in piezoelectric material under impact［J］.International Journal of Solids and Structures，2007，44（25－26）：8457－8492.

［7］JIN C，WANG X D，ZUO M J.The dynamic behaviour of surface－bonded piezoelectric actuators with debonded adhesive layers ［J］.Acta Mechanica，2010，211（3－4）：215－235.

［8］Irwin G R.Analysis of stresses and strains near the end of a crack traversing aplate ［J］.Journal of Applied Mechanics，1957，24（3）：361－364.

［9］XIE De，Biggers S B Jr.Strain energy release rate calculation for a moving delamination front of arbitrary shape based on virtual crack closure technique，Part I：Formulation and validation ［J］.Engineering Fracture Mechanics，2006，73（6）：771－778.