矢量声纳高速运动目标稳健高分辨方位估计*

2013-09-27梁国龙马巍范展王逸林

物理学报 2013年14期

梁国龙马巍范展王逸林

(哈尔滨工程大学,水声技术重点实验室,哈尔滨 150001)

(2012年11月28日收到;2013年1月31日收到修改稿)

1 引言

作为水下作战平台近乎惟一的“耳目”,利用水下声信息进行探测、识别、定位、导航和通信的广义声纳系统,在容许的应用环境中大多采用声纳阵列的形式进行所需信号处理,以获得可控的阵列指向性和较高的空间处理增益.空间谱估计是水声阵列信号处理最主要的研究方向之一,其旨在研究空间多传感器阵列声纳所构成的处理系统对感兴趣的空间信号参数进行准确估计的能力,主要用于估计信号的空域参数或信源位置.近些年来,随着声矢量传感器技术在理论分析、性能评估和工程实践上的研究应用迅猛发展,基于声矢量传感器的方位(direction of arrival,DOA)估计技术得到较为深入的研究[1-7].以多重信号分类(multiple signal classifi cation,MUSIC)算法为代表的大多数高分辨子空间类算法[8-10],由于需要对接收数据协方差矩阵进行有效估计,对于空域接收数据快拍数提出了较高的要求.然而对于大多数有意义的应用环境而言,大快拍数据往往不易得到.特别是对于声纳阵列的实际作战应用环境中,大量出现的是高速运动目标或瞬态信号,战机往往转瞬即逝,此时获取的有意义数据快拍通常较少,极恶劣情况下其有效数据甚至可能出现单快拍情况,上述的高分辨算法将由于得不到有效的协方差估计矩阵而失效.为了解决小快拍数条件下的稳健高分辨DOA估计问题,Sarkar等[11-14]提出了直接数据域方法(direct data domain,DDD),与传统统计方法相比,它具有单快拍处理的优势,且避免了样本协方差矩阵的构造及求逆运算.文献[15—19]的压缩感知理论(compressive sensing,CS)利用信号稀疏特性可对原始信号进行重构;Maliotov等[20,21]以类似的思想提出利用信号稀疏分解进行DOA估计的方法;付金山[22]将信号稀疏分解理论运用到了矢量传感器阵列信号处理中.

上述方法大多需要较高的输入信噪比门限,否则其估计性能将大幅下降.然而在矢量声纳阵列应用环境下,信噪比与快拍数一样往往不能达到较理想的状况.针对这样的限制条件,本文利用声矢量传感器的结构特性,引入空域滤波技术[23],提出将声压振速联合处理技术与空域滤波技术联合使用的时空滤波压缩感知DOA估计方法,大大减小了输入信噪比门限,同时利用小快拍数据可有效估计高速运动目标或瞬态信号的瞬时方位,具有较强的鲁棒性.

2 声矢量传感器基本原理

2.1 声矢量传感器模型

矢量传感器由声压水听器和质点振速水听器复合而成.声压水听器测量空间的声压P,质点振速水听器测量声场中的质点振动速度Vx,Vy,因此矢量传感器可以共点、同步测量声场的声压标量和质点振速矢量.典型的声矢量传感器如图1所示.

图1 声矢量传感器模型

均匀各向同性的非黏滞流体传播介质中,Euler方程可以写成

其中,p(r,t)表示t时刻声场中r位置处的声压,v(r,t)代表该点处的振速,ρ表示介质密度.考虑远场平面波条件,则声压函数可以写成

其中,uT=[sin(θ)cos(φ),sin(θ)sin(φ),cos(φ)]代表声矢量传感器的方向向量,θ和φ分别表示信号的水平方位角和垂直俯仰角,C代表介质中的声速.进而可将声压梯度表示为

对于声波传播背景而言,线性化(1)式,并可忽略其中的振动加速度项,结合以上各式可得：

其中,Z=ρC表示平面波波阻抗.

不失一般性,考虑二维声矢量传感器模型,则其声压振速3通道接收数据模型可以描述为

其中,s(t)为原始信源数据,np,nvx,nvy分别为各通道噪声.

2.2 声矢量传感器阵列测量模型

考虑二维各向同性噪声场中,远场窄带信源入射到任意几何形状矢量声纳阵列,假设阵元数为M,信源数为N(N＜M).各信源中心频率为 fl,入射角度为θl,l=1,2,···,N,定义为信源与声矢量传感器阵列法向夹角.以阵列最左端阵元为参考坐标系原点,则阵列接收的快拍数据可以表示为

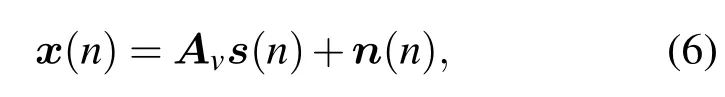
其中,

Av为导向矢量矩阵,a(θl)为第l个信源在传感器阵列上的阵列流型矢量,kl为第l个入射信源的波数,rq代表第q个阵元的空间位置矢量,u(θl)表示第l个信源的方向矢量.

3 声矢量传感器声压振速联合时域滤波方法设计

(5)式描述的声矢量传感器的结构特性表明,均匀无限介质中平面波相干辐射源声场内部,声压与振速各通道信号完全相关.平面波声场中,波阻抗Z=ρC为实数,因而相干信号的声压与振速相位是相同或相反的.

与之不同的是在各向同性噪声场中,假设np(t)为入射角不同的 j个互不相关各态历经随机噪声声压,且满足,则其水平、垂直振速可以表示为

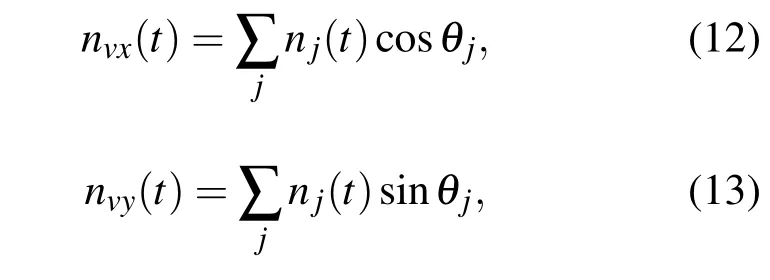
其中,θj为[0,2π]内均匀分布的随机变量.声压与振速的相关系数可以表示为

分√别记声压与两振速标准差之积为kpvi=整理可得：

即各向同性噪声场中声压与振速相关系数为0.这意味着在上述信号、噪声场中,对于声矢量信号的声压振速联合处理对于噪声具有抑制作用.

对于声矢量传感器数据通道做旋转组合变换,定义旋转变换后数据为

整理(13)式并注意到(5)式可得：

其中,φ为电子旋转角.将声压通道数据与上述旋转变换数据进行组合,采用(p+vc)vc的组合形式,考虑上述信号噪声相关特性,其一阶矩可表示为

这意味着通过将声矢量传感器数据进行旋转组合,并选择合适的旋转角φ可以减小噪声,从而降低信噪比门限,为探索远距离微弱目标提供了可能.图2给出了旋转角为60°时,旋转组合后单个声矢量传感器的指向性图.

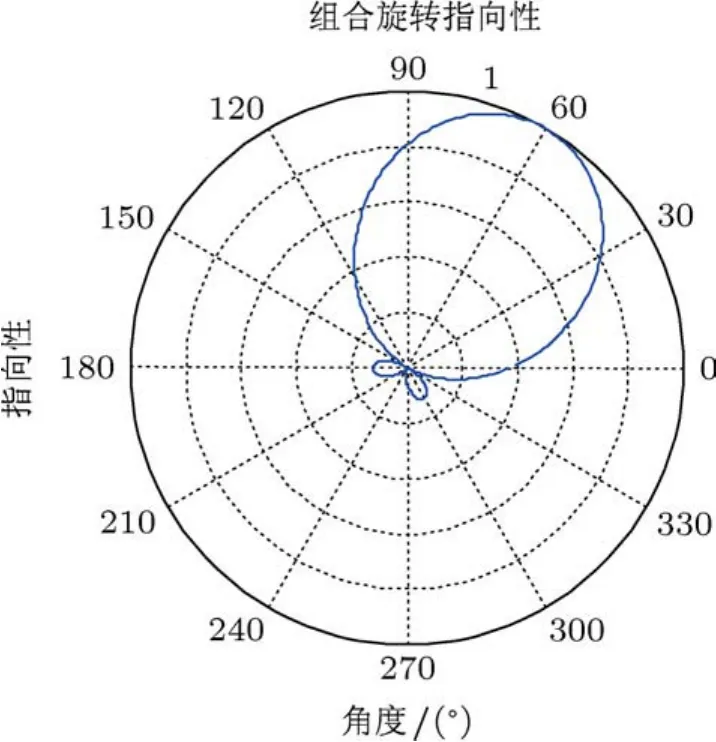
图2 以60°组合旋转后的指向性图

利用信噪相关特性上的差异进行降噪处理,因而声压振速联合处理抗噪方式属于一种广义时域滤波.

4 阻带衰减通带均方误差最大值最小矩阵空域滤波器设计

矩阵空域滤波技术(matrix filter,MF)是一种阵元域数据预处理算法,通过设计阻带与通带扇面的空域幅频响应实现对信号的预滤波,从而降低信号处理信噪比门限.考虑2.2节所述声矢量传感器阵列模型,设计滤波矩阵F对输入数据进行空域滤波,则(6)式改写为

其中,Fv=FHAv表示矩阵滤波后的声量传感器阵列流型矩阵,nF(n)=Fvn(n)表示矩阵滤波后的噪声数据矩阵.MF方法的基本思想是设计矩阵滤波器,使其空域幅频响应满足对于空域预成方位扇面保证无失真通过,对于其他方位扇面形成某可控衰减,即为空域带通滤波器.其思想可以表述为

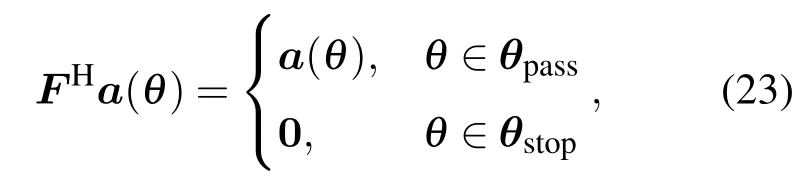
其中θpass,θstop分别表示空域滤波器的理想通带与阻带.我们希望设计出的矩阵滤波器可以满足在通带内由其与原始阵列流型组合产生的新阵列流型变化的均方误差最大值最小,在阻带扇面内将输出功率减至某指定值.按照这样的思想,矩阵滤波器优化设计问题可以表述为

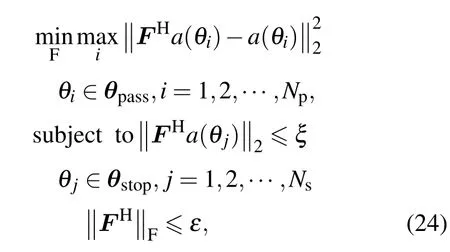
其中,i,j分别代表通带与阻带内的离散方位分辨率,Np,Ns分别表示通带与阻带扇面内离散出的方位个数,‖·‖F表示Frobenius范数,ξ为阻带内的衰减率,ε为滤波后噪声功率门限.上述优化问题可参考文献[23]给出的方法,将滤波器设计转化成二阶锥规划问题进行求解.

5 时空联合滤波压缩感知方位估计

压缩感知技术利用信号在某域的稀疏特性,通过构造观测基或冗余字典对信号进行非自适应随机投影测量,随后通过求解L范数优化问题使信源信号能够以很高的概率精确重建.将CS技术做适宜水声矢量信号处理框架的变形,联合前文提出的时域和空域滤波方法,采用CS技术进行矢量声纳空间谱估计,理论上可以大大减小所需的处理信噪比门限,并在小快拍数情况下取得较好估计效果.

5.1 矢量声纳阵列空间谱稀疏性分析

不失一般性,考虑水声环境中水平均匀半波间隔矢量声纳直线阵,其余条件如2.2节所述.对于(6)式的基本模型而言,s(n)为N×α维,α表示空域采样快拍数,其含义为空间每信源α点采样的N个原始信源集合.如果将全空间方位离散化,并假设离散分辨率为η,(η＞0),则s(n)必可表示为全空间方位中round(2π/η)个离散角度信源的线性组合,round(·)表示对变量取整.其在对应的目标θi角度中表示系数1,其他方位为0.省略宗量n,上述原理的数学表述为

其中,β为round(2π/η)×α维空域稀疏表示系数,ψ为N×round(2π/η)维空域稀疏变换基.通过设置合适的空域分辨率η,可满足N≪round(2π/η),即保证了β是空域N行稀疏的.图3为上述变换的示意图,其中实心圆点代表真实目标,空心圆点代表空域离散点.

图3 矢量声纳空域稀疏分解示意图

从另一个角度而言,根据(8)式矢量声纳阵列空间数据接收模型可认为是空域有限复单频信号的叠加,因而原始数据经空域傅里叶变换到空间域中,其表示系数也必然是稀疏的.

5.2 矢量声纳阵列压缩感知方位估计方法感知矩阵的构建

CS理论对于观测基的选取要求其与稀疏基不相关,这里的相关性可以理解为相互表示时所需的表示系数个数,非相关性越强,利用CS理论进行稀疏系数优化求解的成功概率就越高.考虑对空间信号进行随机采样,即将矢量声纳进行随机布放,因而声压振速各通道的接收数据可认为是对原始信号s的行随机抽取,可表述为

其中,R表示上述定义的行随机矩阵.利用(24)式可得：

Θ为原始信号稀疏至空域后的行随机抽取矩阵.布阵方式导致的矢量声纳阵列流型随机性可看作对稀疏信号的行随机投影测量,因而其与稀疏基具有很强的非相关性.这样的非相关性与约束等距条件(restricted isometry property,RIP)是等价的,二者都是可精确重构稀疏信号的充分条件,因而保证了矢量声纳压缩感知DOA方法的稳健性.实际应用中,当随机布阵结束后,利用已知的阵元位置可精确得到阵列流型矩阵Av,并与空域滤波矩阵相乘得到新的阵列流型Fv,进而构建全部从0至round(2π/η)方位的阵列流型作为过完备冗余字典即可得到感知矩阵Θ.

5.3 矢量声纳阵列时空联合滤波压缩感知方位估计方法

分别利用前述的旋转组合时域滤波方法和矩阵空域预滤波方法进行预处理后,矢量声纳阵列时空联合滤波压缩感知方位估计方法(vector sonar array time space fi ltered compressive sensing DOA,VTSCS)的基本原理可以表述为已知输入阵列接收数据x和人为构造的空域过完备冗余字典Θ,求解(26)式中信号稀疏表示β的问题.一个比较自然的想法是求解下述0范数最优化问题：

其中0范数代表稀疏表示β中非零项的个数,然而这是一个NP-HARD问题,精确解的获得需要遍历所有的可能解,从而使计算复杂性大大增强.文献[17]表明如果采用1范数代替0范数进行优化求解,则可得到如下的凸优化问题：

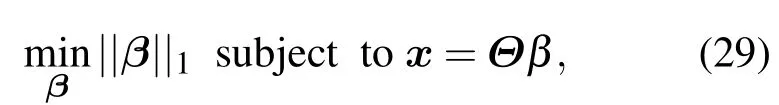
且在满足一定条件时,上述两式是等价的.考虑含噪声的情况下,可改写(28)式为如下的凸优化问题：

其中,σn2是对噪声功率的一个估值.实际应用中,可采用一阶递归滤波的形式对当前噪声功率进行实时在线估计.

需要说明的是,(29)式对于单快拍情况是典型的凸优化表示,因而具有良好的优化解.而对于多快拍联合估计,(29)式是非凸的,应考虑将多快拍数据进行综合处理,即将其考虑成各单快拍数据的组合,进而将估计得到的稀疏表示结果β表示成利用各单快拍估计得到的结果的加权形式,即

其中,βi表示利用第i个快拍数据估计得到的稀疏表示结果,ϑi为利用第i个快拍数据估值的惩罚因子,表示目标高速运动时可利用的当前快拍数据的置信程度,满足ϑi∈[0,1].联合求解(29),(30)式即可得到原始信号的空域稀疏表示,由于其是空域N行稀疏的,因而β中N个非零项的对应位置与空域分辨率之积即为目标的DOA值.图4所示为VTSCS方法的信号处理流程.

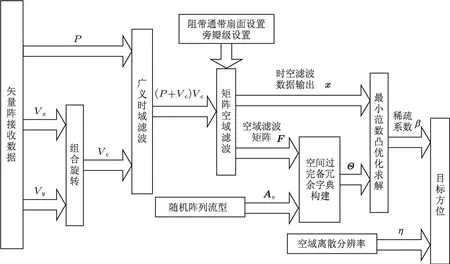
图4 VTSCS方法信号处理流程图

此外对于宽带形式信号,可对原始时域信号做傅里叶变换,进而在得到的每个频域子窄带上采用VTSCS方法进行DOA估计.

6 数值仿真试验分析

考虑各向同性噪声场中,远场等功率非相干窄带双目标入射至10元矢量声纳随机阵型阵列.入射角度分别为30°,50°,频率分别为1 kHz,2 kHz,采样频率10 kHz,输入信噪比为20 dB,快拍数为200.如无特殊说明,均采用以上基本试验条件.为便于分析说明仿真结果,分别将VTSCS方法与基于矢量常规波束形成的DOA估计方法(vector conventional beamforming,VCBF)、矢量最小方差无畸变响应方法(vector minimum variance distortionlessresponse,VMVDR)和矢量MUSIC方法(vector MUSIC,VMUSIC)进行DOA估计性能比较.其中,图5给出了各种方法DOA估计的谱峰显示,图6—8分别给出了以信噪比、快拍数和信源入射角度间隔为变量时的DOA估计性能.性能优劣评价标准除可视的谱峰输出外,根据变化条件的不同,主要考察各方法多次DOA估计的均方根偏差(root mean squareerror,RMSE)或成功概率(success probability,SP).

定义N 次信源方位估计的RMSE为

其中,θij和分别表示第i个信源第 j次试验的真值和估计值.

SP即为成功的估计次数占估计总数的百分比.

图5给出了前述基本条件下各种方法的空间谱估计图.从中可以看出当信噪比与快拍数均较高时,除VCBF方法估计性能较差外,其余各种方法均能给出目标较准确的方位估计,其中VTSCS方法的可分辨信噪比门限要远低于前述各种方法.

图6给出了快拍数为200,入射角度间隔20°时各种方法RMSE随信噪比变化示意图.从插图中可以看出在低信噪比条件下,VTSCS比其他方法具有更好的DOA估计性能.随着信噪比的逐渐增加,各种方法的估计RMSE逐渐减小.其中VMUSIC方法的RMSE最小,VTSCS方法略逊于VMUSIC.考虑到较高信噪比时VTSCS的估计RMSE仅比VMUSIC方法大0.02°左右,因此可认为VTSCS方法与VMUSIC方法具有类似的DOA估计精度,在高信噪比条件时近似是无偏估计.

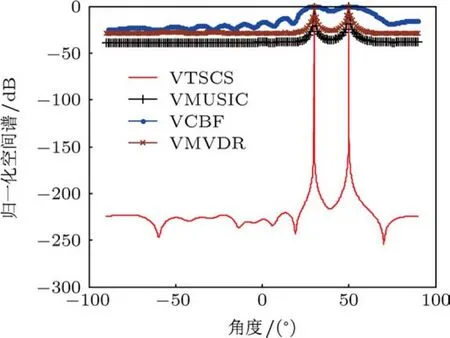
图5 DOA估计性能比较图

图6 不同信噪比条件下各种方法估计均方根偏差比较

图7 给出了信噪比0 dB,入射角度间隔20°时各种方法RMSE随快拍数变化示意图.从插图中可以看出VTSCS方法对快拍数不敏感,在单快拍情况下其RMSE仍只有0.5°左右,具有较强的稳健性.其他各方法估计性能都受到快拍数的限制,其中在较低快拍数情况下,由于子空间分解对于快拍数有着更高的要求,VMUSIC方法具有比VMVDR方法更大的RMSE,而随着快拍数的逐渐增加,VMUSIC方法RMSE逐渐减小.VTSCS方法始终具有最低的DOA估计RMSE.

图8给出了信噪比0 dB,快拍数为200时各种方法SP随入射角度间隔变化示意图.从中可以看出随着入射信源角度间隔的增加,各种方法的估计成功概率都有所提高.其中,VTSCS方法对于角度间隔具有最好的稳健性,在约5°双目标分辨概率可达90%,VMUSIC方法的角度分辨力要强于VMVDR方法和VCBF方法.

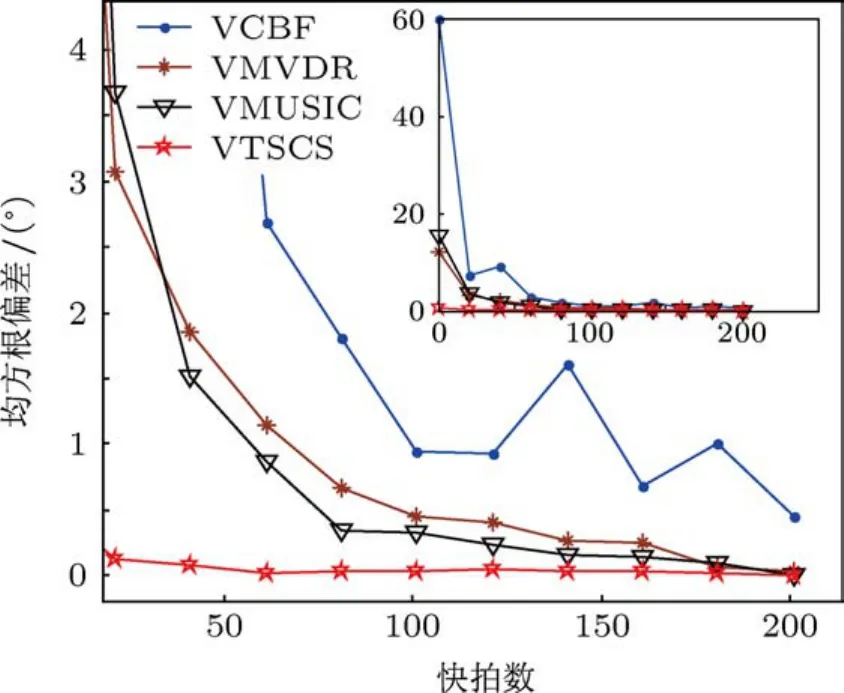
图7 不同快拍数条件下各种方法估计均方根偏差比较

图8 不同入射信源角度间隔条件下各种方法估计成功概率比较

图9 单快拍条件下各种方法空间谱图

考虑矢量声纳阵应用背景下双目标高速运动的极端情况,即假定只有单快拍数据有效,其余基本条件不变.图9给出了此时上述各种方法的空间谱图.可以看出,由于VMVDR和VMUSIC方法的DOA估计性能严重依赖于数据协方差矩阵的估计程度,因此对于单快拍情况,这两种方法已经失效.此时,VTSCS方法仍具有较高的双目标分辨门限,但估计精度有所下降.值得说明的是,虽然在前述各种条件下的性能比较时VCBF方法的性能总是最差,但此时仍具有一定的双目标分辨能力,因而VCBF方法也具有较强的鲁棒性.

7 湖上试验验证

为验证VTSCS方法的有效性,于某自然水域进行了相关试验.试验采用6元矢量阵,布放于测量船下深度约10 m,阵间距1.5 m.两非相关窄带声源布于同深度,距离6元阵声中心距离100 m左右,入射角约为20°,74°,频率分别为1 kHz,2 kHz,系统采样频率20 kHz,阵列输入信噪比约为10 dB.图10所示为系统构建示意图.

图10 湖上试验示意图

取单快拍数据,利用一阶递归方法估计当前噪声功率,并设置(30)式中合适的噪声功率门限值.对此数据分别利用VCBF,VMVDR,VMUSIC和VTSCS方法进行DOA估计,其空间谱输出如图11所示.

从图中可以看出,与理论分析一致,单快拍时VMUSIC与VMVDR方法均已失效.VCBF方法具有分辨双目标的能力,但精度不高.VTSCS方法具有较好的双目标分辨门限,但此时精度也已降低,其RMSE约为4°.

值得说明的是,噪声功率门限的设定对于VTSCS方法的性能有着重要影响.图12和图13分别给出了噪声功率门限设置过低和过高时VTSCS方法的空间谱图.

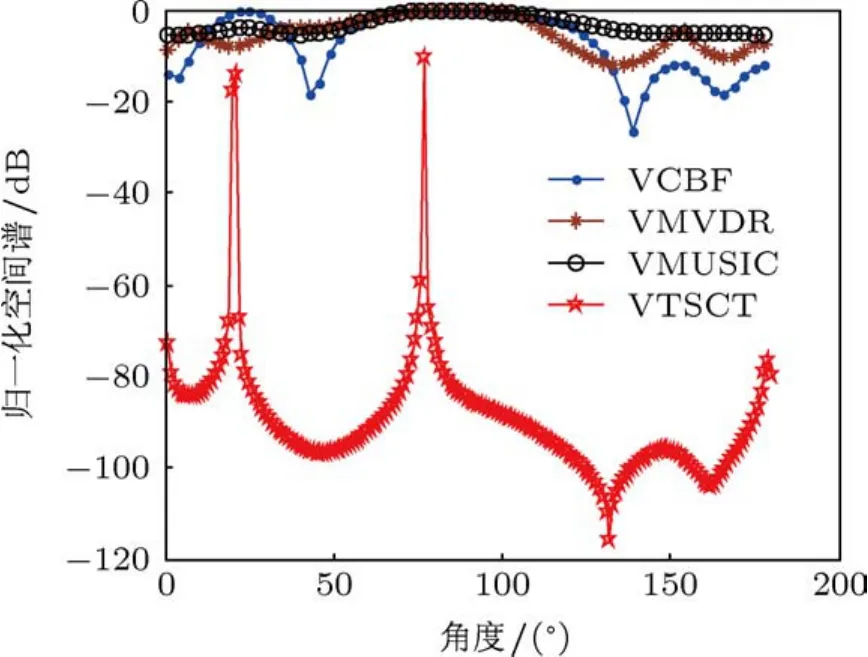
图11 湖上试验空间谱图

图12 噪声功率门限过低时VTSCS空间谱图

湖试结果表明,当噪声功率设置过低时,意味着提高了对于(30)式中可存在的噪声功率的要求,即对凸优化求解过程的限制条件更苛刻.此时利用凸优化可能无法得到全局最优解,进而会用一系列的局部最优值来进行替代,因而会出现一系列伪峰.当噪声功率设置过高时,对于(30)式中噪声功率的约束过小,噪声的存在将严重影响信源的空域稀疏性,因而无法得到正确的DOA估计.

图13 噪声功率门限过高时VTSCS空间谱图

8 结论

提出了一种矢量声纳阵高速运动目标稳健高分辨方位估计方法.该方法分别利用声矢量传感器声压振速联合处理的广义时域滤波和阻带约束通带均方误差最大值最小矩阵空域滤波进行前置处理,进而利用矢量阵空域目标稀疏特性,结合压缩感知理论进行空间谱估计.理论分析与数值仿真表明,与经典的VCBF,VMVDR,VMUSIC方法相比,新方法利用小快拍数据即可获得较低的双目标分辨门限和较高的估计精度,具有较高的小快拍(单快拍)数据DOA估计稳健性,为远程微弱高速运动目标的方位估计问题提供了新的解决思路.湖试结果验证了该方法的有效性.

[1]Nehorai A,Paldi E 1994 IEEETrans.on SP 42 2481

[2]Hui JY,Liu H,Yu H B,Fan M Y 2000 Acta Acustica 25 303(in Chinese)[惠俊英,刘宏,余华兵,范敏毅2000声学学报25 303]

[3]Shi J,Yang D S,Shi SG 2012 Acta Phys.Sin.61 4302(in Chinese)[时洁,杨德森,时胜国2012物理学报61 4302]

[4]Yang SE 2003 J.Harbin Engin.Univ.24 591(in Chinese)[杨士莪2003哈尔滨工程大学学报24 591]

[5]Wu Y Q 2011 Ph.D.Dissertation(Changsha：National University of Defense Technology)(in Chinese)[吴艳群2011博士学位论文(长沙：国防科学技术大学)]

[6]Sun GQ,Li QH 2004 Acta Acustica 29 491(in Chinese)[孙贵青,李启虎2004声学学报24 491]

[7]Chen X H 2004 Ph.D.Dissertation(Harbin：Harbin Engineering University)(in Chinese)[陈新华2004博士学位论文(哈尔滨：哈尔滨工程大学)]

[8]Schmidt RO 1986 IEEETrans.on AP 34 276

[9]Capon J1969 Proceedingsof the IEEE 57 1408

[10]Roy R,Kailath T 1989 IEEETrans.on ASAP 37 984

[11]Sarkar T K,Sangruji N 1989 IEEETrans.on ASAP 37 940

[12]Sarkar T K 2003 Smart Antennas(1st Ed.)(New Jersey：John Wiley&Sons Inc.)p52