合金团簇(FeCr)n中的非共线磁序和自旋轨道耦合效应*
2013-09-27张宝龙王东红杨致刘瑞萍李秀燕
张宝龙 王东红 杨致 刘瑞萍 李秀燕
(太原理工大学,新型传感器与智能控制教育部重点实验室,物理与光电工程学院,太原 030024)
(2013年2月28日收到;2013年3月29日收到修改稿)
1 引言
众所周知,与相应的固体单晶相比,过渡金属原子组成的小尺寸团簇往往具有不同的几何结构和磁学性质[1-6].一般认为这些奇特的性质起源于体系有限的尺寸、较低的维度和较大的比表面积.
在众多的团簇研究中,Mn团簇占有重要地位.由于Mn原子的价电子结构为3d54s2,其半满的d壳层使得原子具有较大的局域磁矩和复杂的成键能力,因此Mn团簇很早便引起了广泛关注[7-14].实验上已经利用激光蒸发合成法合成了不同尺寸的Mn团簇,并测量了其光学性质[7,8].随后,Knickelbein[9]进一步研究了Mn团簇的磁性.理论上对Mn团簇也有较多研究[10-14].特别是Longo等[12,13]认为某些尺寸的Mn团簇具有非共线磁序.而Kabir等[14]的研究则进一步表明随着尺寸的增加,Mn团簇会发生共线磁序向非共线磁序的“相变”.
除了Mn团簇外,其他过渡金属团簇也可以展现出非共线磁性.例如Kohl和Bertsch[15]以及Tatsuki等[16]分别在小尺寸Fe和Cr团簇中发现了非共线磁性.更为有趣的是,最近的研究表明Fe-Mn和Co-Mn合金团簇也具有非共线磁性[17,18].由于合金团簇可以展示出更为丰富的几何结构、电子结构以及更为奇特的磁学性质,因此对其进行进一步的研究是有必要的.
基于密度泛函理论(DFT),本文对(FeCr)n(n≤6)合金团簇进行了系统的研究.对该体系的研究基于以下几点考虑.首先,如前所述在Mn团簇及相应的合金团簇中均发现了非共线磁序.由于两个Mn原子与一个FeCr二聚体电子数相同,因此(FeCr)n团簇与相同尺寸的Mn团簇互为等电子体.根据等电子体原理[19],等电子体的某些物理和化学性质往往是类似的.因此研究该体系有利于发现新的非共线磁性团簇.其次,先前对合金团簇的研究无论是共线磁性体系还是非共线磁性体系均未考虑自旋轨道耦合(SOC)效应.一般认为3d过渡金属中SOC效应比较弱,所以研究中对此经常予以忽略并认为体系的磁矩完全由自旋磁矩提供.我们的计算却表明,至少对于某些尺寸的(FeCr)n合金团簇,轨道磁矩对总磁矩的贡献比较显著,因而不能忽略.最后,由于不同种类的Fe-Cr合金材料已经在实验上合成[20-23],并且在其合金中观察到了自旋玻璃现象[22],因此对小尺寸合金团簇的研究将有利于理解体相合金中自旋玻璃现象的微观机制.
2 计算方法
全部计算基于Vienna ab-initio simulation package(VASP)程序包[24].计算采用广义梯度近似下的Predew-Burke-Ernzerhof(PBE)交换关联泛函[25]和投影缀加平面波(PAW)方法[26].具体计算使用超胞法,即团簇被放在棱长为15˚A的立方超胞内进行结构优化.由于这里考虑的团簇尺寸较小而超胞边长足够大,因此团簇与其周期镜像间的相互作用可以忽略.进行结构优化时K点选择布里渊区的原点(Γ点)、平面波截断能经测试后取为400 eV,能量收敛标准为10-5eV.此外,对于每一个尺寸的团簇考虑各种可能的初始结构.对于每个初始结构则考虑不同的共线磁序(CL)和非共线磁序(NCL),例如在CL情况下我们具体考虑了非磁(NM)、铁磁(FM)和反铁磁(AFM)几种情况.最后选择能量最低的结构为体系的基态.计算时还充分考虑了SOC效应对体系结构和磁性的影响.
尽管本文使用的超胞法已经被广泛地用来研究小团簇的几何结构和电子结构[10,12-14,17,18,27],但为了进一步验证所选择计算参数的合理性,我们计算了Fe2和Cr2二聚体的键长和磁矩.计算结果表明基态Fe2的磁序为FM,相应的键长和总磁矩分别为2.00˚A和5.950µB,与先前的结果一致(FM基态,键长1.961˚A,总磁矩6.00µB)[16].基态Cr2的磁序为AFM,相应的键长和总磁矩分别为1.750˚A和0µB,也与先前的结果一致(AFM基态,键长1.723˚A,总磁矩0µB)[15].因此这里选择的计算参数是合理的,可以用来描述Fe-Fe和Cr-Cr原子间的相互作用.
3 结果与讨论
3.1 团簇的结构、磁序和稳定性
(FeCr)n(n≤6)合金团簇的基态和某些亚稳态结构在图1中给出,图中序号根据总能量由低到高排列,如(n a)代表尺寸为n的团簇的基态结构.同时基态团簇的对称性、磁序和结合能等参数在表1中给出.这里,结合能的计算公式为
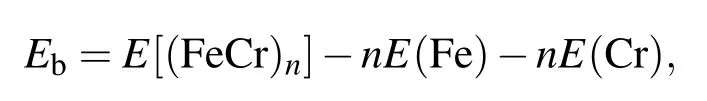
式中E[(FeCr)n],E(Fe)和E(Cr)分别代表(FeCr)n团簇,Fe原子和Cr原子的能量.从图1可以看到,所有稳定的团簇都具有较低的对称性.
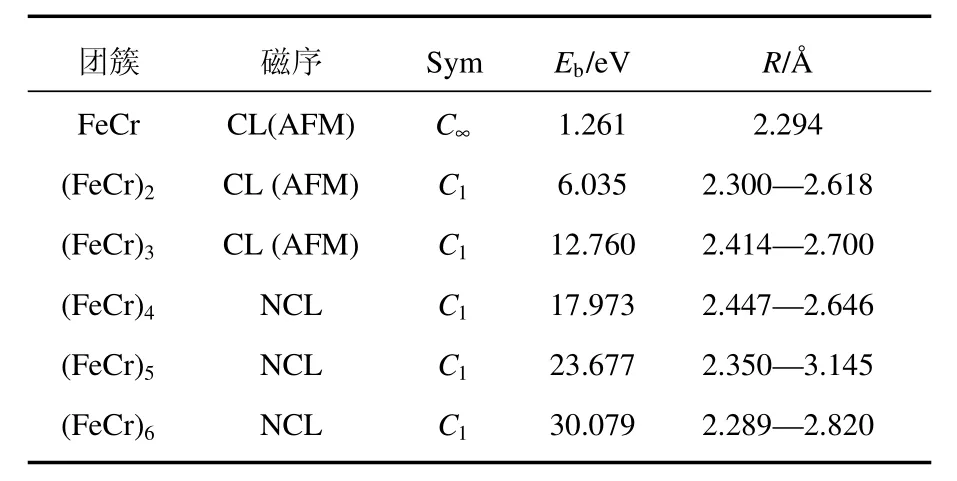
表1 基态团簇的磁序,对称性Sym,结合能E b/eV和Fe—Cr键长范围R/˚A
FeCr二聚体是本文研究的最小的合金团簇.虽然Fe2的磁序为FM,Cr2的磁序为AFM,但FeCr的磁序为AFM.表明Fe原子和Cr原子倾向于反铁磁耦合.这种反铁磁耦合在更大尺寸的(FeCr)2和(FeCr)3基态中也被观察到.从图1及表1可以看到,FeCr的总磁矩为1.746µB,键长为2.294˚A,与Ma等[28]用全电子DFT计算的结果一致(AFM基态,总磁矩2.00µB,键长2.308˚A).这也表明本文所使用的计算参数能够合理描述Fe-Cr原子间的相互作用,因而可以应用到更大尺寸的体系上.有趣的是,其等电子体Mn2的磁序为FM[11,12],与FeCr的磁序并不相同.不过FeCr二聚体也可展示出FM磁序(见图1中1b),但相应的能量比AFM高出0.406 eV.此外,对于该二聚体我们没有发现非共线磁结构.
对于n=2和3的合金团簇,计算结果表明基态团簇的磁序也是AFM.并且在基态和亚稳态中均未出现非共线磁序的情况.但是某些过渡金属团簇,例如Fe团簇在三聚体时就出现了非共线磁性[16].对于(FeCr)2,其基态为C1对称性的平面四边形,相应的结合能为6.035 eV.2b,2c和2d等亚稳结构均为畸变的四边形,具有较低的结合能.对于(FeCr)3,其基态是C1对称性的AFM三角反棱柱,相应的总磁矩为5.442µB.第一亚稳态3b也是一个三角反棱柱,但是却具有明显高于基态的能量(ΔE=0.796 eV)和较大的总磁矩(Mtot=13.442µB).

图1 (FeCr)n(n≤6)合金团簇的基态及若干亚稳态结构 ΔE表示相应结构相对于基态结构的能量差,M tot表示总磁矩;图中1a—6a分别为代表尺寸为n的团簇的基态结构
图2 给出了(FeCr)n合金团簇的总磁矩随尺寸的变化曲线,Mn团簇的结果也一并给出.图中展现的一个显著的特点是(FeCr)n团簇总磁矩的变化趋势与相应等电子体Mn团簇的变化趋势基本相同.例如都是在四聚体处出现了峰值,随后磁矩逐渐减小.不同的是,Mn6团簇就出现了非共线磁性,但相应的(FeCr)3团簇基态仍然是共线AFM序.两种团簇磁矩变化趋势相似或许是由于二者为等电子体,因此可以展示出某些类似的物理和化学性质.至于非共线磁性出现的尺寸不同则可能是由于Fe—Cr键与Mn—Mn键本质上不同引起的.
随着尺寸的增加,(FeCr)n体系的磁性发生了根本的变化.对于(FeCr)4,结果表明其基态具有非共线磁序,相应的总磁矩为4.010µB.此外,非共线磁序也在(FeCr)5和(FeCr)6的基态中被发现.因此在(FeCr)n合金团簇中随着尺寸的增大,在n=4处发生了共线到非共线的磁序“相变”.从图2可以看到Mn8也具有非共线磁序,但相应的总磁矩更大[14].有趣的是,(FeCr)4的第二个同分异构体4b与基态4a结构类似,但却具有共线AFM序,能量比基态高约0.3 eV.这表明对于小尺寸团簇来说,考虑可能的非共线磁序很有必要,否则可能会丢失能量更低的状态.类似的情况也在n=5和6中被发现.
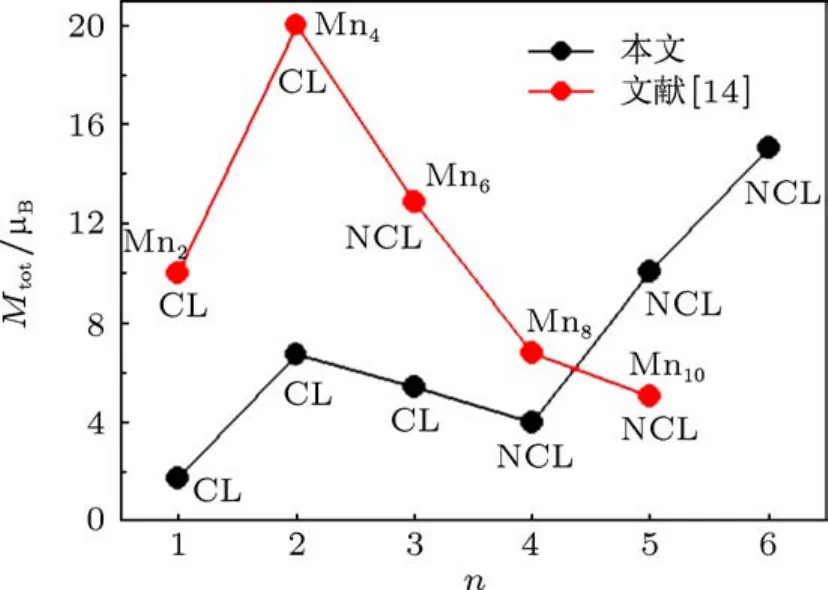
图2 基态(FeCr)n团簇和等电子体M n团簇总磁矩随尺寸的变化,图中给出了每个团簇的磁序
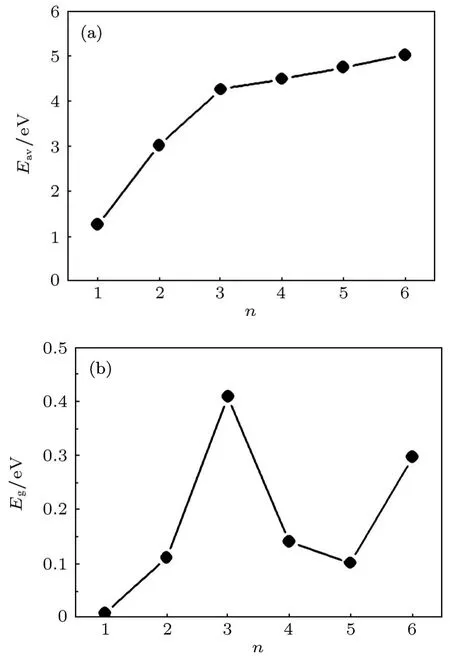
图3 基态团簇的(a)平均结合能E av和(b)HOMO-LUMO能隙E g
尽管(FeCr)5和(FeCr)6团簇的基态也具有非共线磁序,但两者却具有明显大于(FeCr)4的总磁矩.对于n=5的情况,除了5d外,基态5a和其他两个亚稳态5b和5c都是畸变的四带帽八面体.(FeCr)5基态总磁矩为10.035µB,比其等电子体Mn10磁矩高(见图2).因此通过对比n=4和5两种情况发现(FeCr)n团簇的总磁矩可以大于或小于相应的Mn团簇,依赖于具体的团簇尺寸.对于(FeCr)6,无论其基态或是亚稳态均为笼状结构.有趣的是,虽然优化中我们选取了不同的构型,但是很多构型最终都收敛到了6a,表明该结构的确是基态.
为了分析合金团簇的热力学稳定性和动力学稳定性,图3中给出了平均结合能和最高占据轨道(HOMO)与最低未占据轨道(LUMO)之间的能隙.这里平均结合能的定义为Eav=Eb/n,Eb已经在表1中给出.从图3(a)可以看到,随着团簇尺寸的增加,体系的平均结合能单调增加,说明团簇的生长过程是一个不断放热的过程,所有团簇在热力学上都是稳定的.在所研究的范围内团簇尺寸越大,热力学稳定性就越高.
此外,团簇HOMO与LUMO之间的能隙Eg是一个重要的物理量,它可以在一定程度上描述体系中电子跃迁的难易,因此可以定性地反映团簇的动力学稳定性和化学活性[29].从图3(b)可以看到,由于团簇的能隙都比较小(<0.5 eV),所以这里研究的所有合金团簇的动力学稳定性都比较低、化学活性比较强.更为重要的是,团簇的动力学稳定性随着尺寸变化展现出复杂的行为.FeCr的稳定性最低而(FeCr)3的稳定性则相对较高.较高的热力学稳定性和较强的化学活性表明(FeCr)n合金团簇或许可以被用作一种新的催化剂.
3.2 团簇的自旋磁矩、轨道磁矩和SOC效应
为了进一步分析合金团簇的磁性,表2给出了基态团簇的自旋总磁矩、轨道总磁矩和各个方向的磁矩分量.自旋总磁矩和轨道总磁矩分别为各个方向上相应磁矩分量的平方和再开方[30].由表2可以看出体系的磁矩有如下几个特点:第一,团簇的总磁矩主要由自旋磁矩来提供,但对于某些小尺团簇轨道磁矩的贡献不能忽略,例如对于(FeCr)4,总磁矩4.010µB(见图1 4a),自旋磁矩为3.741µB,因此忽略轨道磁矩会引起近10%的误差,误差较大,在二聚体FeCr中这个现象更为突出;第二,除了FeCr的x分量外,团簇轨道磁矩的各个分量与相应自旋磁矩的分量方向总是一致的,也就是SOC效应会增强总的磁矩,以(FeCr)3为例,在其x方向,Msx和Mox均沿着负x轴,大小分别为1.693和0.078µB;第三,在n=4时磁矩减小到最小,这是由于团簇的磁序由共线转变为非共线,使得各个原子的磁矩分量在一定程度上相互抵消,导致总磁矩变小.
表2 基态团簇的自旋磁矩和轨道磁矩
为了理解n=4时体系产生共线到非共线磁序“相变”的原因,我们在图4中给出了(FeCr)4团簇4a和4b的总态密度(TDOS)和局域态密度(LDOS).其中LDOS只给出了d电子的结果.如前所述,由于4a和4b的结构基本相同而磁序不同,前者为非共线磁序而后者为共线AFM序,但是4a具有更低的总能量,因此通过比较二者的差别可以揭示为何n=4时体系基态是非共线磁序而不是共线磁序.需要指出的是,与传统的自旋极化计算结果不同,在考虑非共线磁性和SOC的情况下4a结构的TDOS和LDOS无法区分为自旋向上和自旋向下两种自旋状态.为了便于对比,4b结构的态密度则是自旋极化计算的结果.
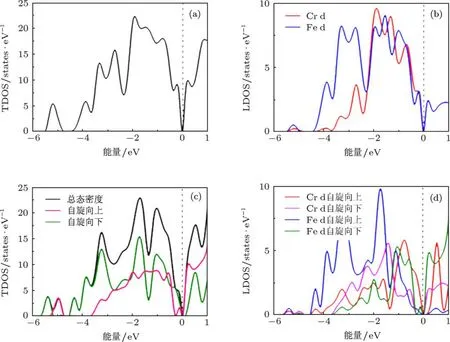
图4 (FeCr)4团簇的总态密度TDOS和局域态密度LDOS 费米能级为能量零点(a),(b)4a结构的TDOS和LDOS;(c),(d)4b结构的TDOS和LDOS
对比TDOS和LDOS可以发现,无论是对非共线磁性4a还是对共线磁性4b,体系费米能级附近的状态主要由过渡金属的d电子态组成.对于基态4a,从图4(b)可以清楚看到Fe的d电子与Cr的d电子有着非常强烈的杂化,特别是在费米能级以下两个电子伏的范围内这种杂化非常显著.但是对共线磁性体系4b,Fe的d电子与Cr的d电子杂化程度则相对较弱.因此Fe原子和Cr原子的d-d杂化是体系出现非共线磁性的根本原因.正是由于这种较强的d-d杂化,有利于(FeCr)4中原子间成键并产生较强的相互作用,从而使体系出现能量更低的非共线磁性状态.类似的现象也在n=5和6的非共线磁性团簇中被发现.另外,先前的研究表明非共线磁序是由于团簇中FM与AFM磁序之间相互竞争产生所谓的“失措”效应引起的[15,18],考虑到失措效应起源于电子之间复杂的相互作用,本文提出的d-d电子杂化机制同先前结论一致并更深入地解释了非共线磁序产生的原因.
为了分析团簇的磁序和成键性质,图5以(FeCr)4为例给出了4a和4b的局域磁矩、三维差分电荷密度和相应的二维差分电荷密度.图5(a1)和(b1)中每个原子旁边的数字标明了Fe或Cr原子的排列序号.表3则给出了两个团簇中每个原子的Bader电荷[31,32].从图5(a1)和(b1)可以看到非共线磁序和共线磁序的局域磁矩方向差异的确非常显著,但两种磁结构下都是Fe原子提供较大的磁矩、Cr原子提供较小的磁矩.另外,虽然磁序有明显的不同,但是从图5(a2)和(b2)中可以看到两者的差分电荷密度基本相同,均为原子失去电子而在不同原子之间形成较强的共价键.这意味着不同磁序下团簇中共价键的成分基本相同,是化学键的主要方面.相应的二维差分电荷密度也证实了这一点.

图5 (a1),(a2)和(a3)分别为4a结构的局域磁矩、三维差分电荷密度图和二维差分电荷密度图;(b1),(b2)和(b3)为4b结构的结果;(a1)和(b1)中原子磁矩的大小与箭头的长度成正比;(a2)和(b2)中绿色区域代表失去电子而红色区域代表得到电子

表3 (FeCr)4基态4a和第一亚稳态4b中各个原子的Bader电荷
不同磁序的团簇除了存在较强的共价键,表3中的Bader电荷表明两个体系中都还存在一定的离子键.对于两种磁序,Bader电荷在Cr原子上总是正的,在Fe原子上总是负的,这与Cr原子的电负性较小而Fe原子的电负性较大一致.由于Fe原子和Cr原子电负性相差不大,因此电子的转移并不显著、离子键相对较弱.以上讨论表明非共线磁性体系和共线磁性体系的成键性质是相同的,都以共价键为主、离子键为辅而与磁序无关.此外,基态4a中Cr原子总是比亚稳态4b中相应的Cr原子失去更多的电子,而4a中的Fe原子总是比4b中相应的Fe原子得到更多的电子,表明4a中的离子键比4b更强,因此4a中Fe原子和Cr原子相互作用更强,这也是4a中Fe原子和Cr原子之间d-d强相互作用的体现.
4 结论
利用密度泛函理论,本文系统地研究了(FeCr)n(n≤6)合金团簇的结构、稳定性和磁学性质.所得结论如下:
1)当n≤3时基态团簇为共线反铁磁序,当n≥4时基态团簇为非共线磁序,在n=4时我们发现了体系由共线到非共线的磁序“相变”,计算表明这种“相变”是由Fe原子和Cr原子之间较强的d-d电子杂化而引起的;
2)磁性计算中我们考虑了SOC效应,结果表明在某些情况下合金团簇中轨道磁矩对总磁矩的贡献还是非常显著的,一般不能忽略,而且SOC效应往往可以增强体系的磁性;
3)共线磁性体系和非共线磁性体系的成键性质是相同的,都以共价键为主、离子键为辅,成键类型与磁序无关.
[1]Liu F,Khanna SN,Jena P 1991 Phys.Rev.B 40 8179
[2]Rodr´ıguez-L´opez JL,Aguilera-Granja F,Michaelian K,Vega A 2003 Phys.Rev.B 67 174413
[3]Zhang X R,Gao C H,Wu L Q,Tang SH 2010 Acta Phys.Sin.59 5429(in Chinese)[张秀荣,高从花,吴礼清,唐师会2010物理学报59 5429]
[4]Wang JL 2007 Phys.Rev.B 75 155422
[5]Haraldsen JT,Barnes T,Sinclair JW,Thompson JR,Sacci RL,Turner JFC 2009 Phys.Rev.B 80 064406
[6]L¨u J,Xu X H,Wu H S 2004 Acta Phys.Sin.53 1050(in Chinese)[吕谨,许小红,武海顺2004物理学报53 1050]
[7]Baumann CA,van Zee RJ,Bhat SV,Weltner W 1983 J.Chem.Phys.78 190
[8]Geoffrey M K,Mark B K 1997 J.Chem.Phys.106 9810
[9]Knickelbein M B 2001 Phys.Rev.Lett.86 5255
[10]Tina M B,Marcel H FS,Vijay K,Yoshiyuki K 2002 Phys.Rev.B 66 064412
[11]Bobadova-Parvanova P,Jackson K A,Srinivas S,Horoi M 2005 J.Chem.Phys.122 014310
[12]Longo RC,Noya EG,Gallego L J2005 Phys.Rev.B 72 174409
[13]Longo R C,Alemany M M G,Ferrer J,Vega A,Gallego L J 2008 J.Chem.Phys.128 114315
[14]Kabir M,Kanhere D G,Mookerjee A 2007 Phys.Rev.B 75 214433
[15]Kohl C,Bertsch GF 1999 Phys.Rev.B 60 4205
[16]Tatsuki O,Alfredo P,Roberto C 1998 Phys.Rev.Lett.80 3622
[17]Longo R C,Alemany M M G,Vega A,Ferrer J,Gallego L J 2008 Nanotechnology 19 245701
[18]Du JL,Shen N F,Zhu L Y,Wang JL 2010 J.Phys.D:Appl.Phys.43 015006
[19]Bent H A 1966 J.Chem.Educ.43 170
[20]Gupta R,Singh Raman RK,Koch C C 2008 Mater.Sci.Eng.A 494 253
[21]Singh Raman RK,Gupta RK,Koch CC 2010 Philos.Mag.90 3233
[22]Drovosekov A B,Kreines N M,Kholin DI 2010 J.Low.Temp.Phys.36 808
[23]Drovosekov A B,Kreines N M,Kholin D I,Korolev A V,Milyaev M A,Romashev L N,Ustinov V V 2008 JETPLett.88 118
[24]Kresse G,Furthm¨uller J1999 Phys.Rev.B 54 11169
[25]Perdew JP,Burke K,Ernzerhof M 1996 Phys.Rev.Lett.77 3865
[26]Kresse G,Joubert D 1999 Phys.Rev.B 59 1758
[27]Lin Q B,Li RQ,Wen Y H,Zhu Z Z 2008 Acta Phys.Sin.57 181(in Chinese)[林秋宝,李仁全,文玉华,朱梓忠2008物理学报57 181]
[28]Ma QM,Xie Z,Wang B R,Liu Y,Li Y C 2011 Solid State Commun.151 806
[29]Wang JL,Zhang X Y,Schleyer PV R,Chen ZF 2008 J.Chem.Phys.128 9810
[30]Ataca C,Cahangirov S,Durgun E,Jang Y R,Ciraci S 2008 Phys.Rev.B 77 214413
[31]Henkelman G,Arnalsson A,J´onsson H 2006 Comput.Mater.Sci.36 354
[32]Zin V,Dabal`a M 2010 Acta Mater.58 311
