拉曼型自由电子激光器中相对论电子运动稳定性的比较研究*

徐勇根 王时建 吉驭嫔 徐竟跃 卢宏 刘晓旭 张世昌2)†

1)(西华大学物理与化学学院物理系,成都 610039)

2)(西南交通大学光电子学研究所,成都 610031)

(2012年10月9日收到;2012年11月7日收到修改稿)

1 引言

与普通激光器不同,自由电子激光器的工作频率主要由电子束的相对论能量因子γ和摇摆器的空间周期λw决定;因此,通过控制某些工作参量,从而改变γ和λw值,实现频率连续可调,原则上可以覆盖从微波至γ射线全波段[1,2].自由电子激光的研究热点之一,就是利用这一优势向普通高功率有源器件(千瓦及以上)难于达到的频谱高、低两极发展.目前,在频谱的高端即短波长方面,2009年美国斯坦福加速器中心(SLAC)实现世界上第一台硬X射线自由电子激光(波长0.15 nm)[3];2011年2月,日本同步辐射研究所的LASER自由电子激光装置,实验波长缩短到0.12 nm[4],据2011年8月在上海召开的第33届国际自由电子激光大会报道,2011年6月该装置受激出光,创造了波长短于0.1 nm的世界最新记录.在频谱的低端即长波长方面,国内外均早已实现兆瓦级毫米波、太赫兹波自由电子激光[5-8].有关自由电子产生相干短波长及长波长电磁辐射的研究在不断开展[9-14].

短波长自由电子激光器采用高能量低密度相对论电子束,属于康普顿型,而长波长自由电子激光器则采用低能量高密度相对论电子束,属于拉曼型.由于拉曼型自由电子激光器使用的电子束的流密度高、能量低,为防止电子束在输运过程中发散,需外加与电子束平行的纵向静磁场来引导电子束输运.早期通常采用导引磁场的方向与电子纵向运动同向,即正向导引磁场.后来,美国麻省理工学院的Conde和Bekefi[6]实验发现,当导引磁场方向与电子束纵向运动方向相反,所获得的输出功率和效率比同向情况高得多.Conde-Bekefi实验揭示了一种新机制,拉曼型自由电子激光器由此分成正向导引磁场和反向导引磁场两大类,其理论和实验研究持续至今.2011年,俄罗斯杜布纳联合核研究所(JINR)和俄罗斯科学院应用物理研究所(IAP)用反向导引磁场自由电子激光装置,开展了高功率射频电磁波对铜质谐振腔表面性能衰退的应用研究[15,16].

无论哪种类型的自由电子激光器,由于其激光增益所需的能量由相对论电子束的动能转化而来,因此电子的运动状态及其运动稳定性对器件的效率和性能至关重要[1,2].影响拉曼型自由电子激光器中电子运动稳定性的诸因素中,摇摆器初始段的绝热压缩磁场以及电子束自身场的作用,显得尤为突出.其中,绝热压缩磁场关系到电子初始阶段的运动及电子束的成型,而高密度低能量束流的自身场所产生的电场力和磁场力也会影响电子束的输运.

已有文献对拉曼型自由电子激光器中电子的运动稳定性进行了不少研究,其中Chen和Davidson[17,18]以及 Spindler和 Renz[19]数值模拟发现,正向导引磁场自由电子激光器中电子束自身场会导致电子的庞加莱截面图出现混沌;Zhang等[20,21]则发现,反向导引磁场自由电子激光器中电子束自身场能使电子运动的封闭相轨道变窄,从而电子的速度离散变小.但是,这些文献或者针对正向导引磁场类型,或者针对反向导引磁场类型,缺乏对这两种类型的对比研究.鉴于此,本文对拉曼型正向导引磁场类和反向导引磁场类自由电子激光器中平衡态电子的运动稳定性进行比较研究.本文所得研究结果对认识自由电子激光物理特性具有一定学术意义,对自由电子激光工程实践具有一定参考价值.

2 数理模型

研究自由电子激光器中电子运动稳定性,最早采用并沿用至今的方法是计算电子相轨道的庞加莱截面图(Poincare´surface-of-section map)[17-22].这种方法的优点是图像反映稳定性很直观、形象;其不足之处是当作用在电子的电磁场稍复杂,就不容易找到恰当的哈密顿函数变换母函数来使正则方程组约化,特别是考虑摇摆器初始段的绝热压缩磁场后,就更难找到足够多的初积分使正则方程组约化(这也是采用庞加莱截面图方法的论文从来没有涉及绝热压缩场对电子运动稳定性影响的原因).

科尔莫戈罗夫熵(Kolmogorov entropy,又名metric entropy或者Lyapunov exponent,以下简称K熵)是研究微分方程解的稳定性的常用方法之一[23,24].具体用到运动的稳定性,就是通过跟踪计算初始条件具有微小差别的两条相轨道之间的距离演化来判断稳定性.文献[25]率先采用K熵方法研究了反向导引磁场自由电子激光器中电子运动稳定性;随后,该方法被应用到康普顿型自放大自发发射(SASE)自由电子激光器中电子运动稳定性的研究[26],以及离子通道电磁波摇摆器自由电子激光器中电子运动稳定性的研究[27].相对于庞加莱截面图方法,K熵方法的计算量更大,但其长处是无论作用于电子的电磁场多么复杂,都可以通过数值计算求解其运动稳定性.

相对论自由电子在任意复杂电磁场E和B作用下的六维相轨道,可从下面通用的六个归一化无量纲一阶常微分方程组求解[2,25,26]：

式中电子速度、矢径、作用于电子的电磁场的归一化表达式为

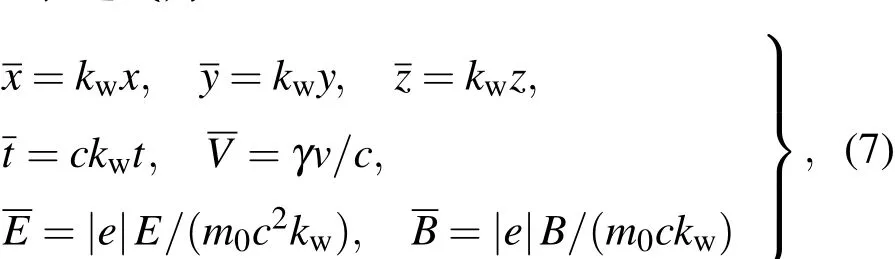
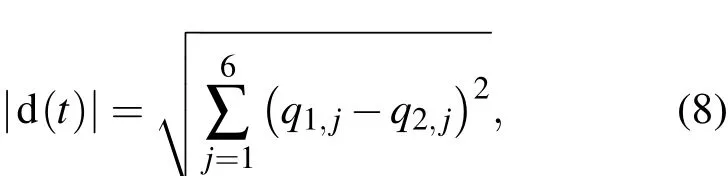
取极限就得到K熵

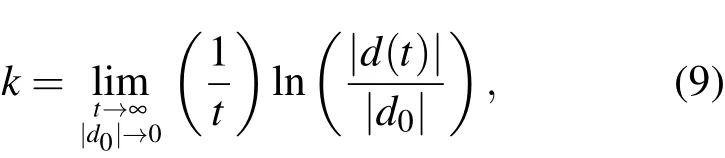
本文考虑作用在电子上的电磁场E和B,包括纵向导引磁场B0,三维螺旋摇摆器磁场Bw,电子束自身磁场Bs和电场Es,其中：

式中︵ez是纵向单位矢量,B0是其幅值(B0＞0与B0＜0分别代表正向与反向导引磁场).考虑到测试电子的运动轨道有可能逸出电子束区域,本文数值计算较之以前文献中的电子束自身场做了改进,采用下面分段函数全面反映束内、束外的自身场[28]：

式中︵eR和︵eφ分别是圆柱坐标系的径向和角向单位矢量,参数Rb和nb是电子束的平均半径和体密度.对于三维螺旋摇摆器磁场

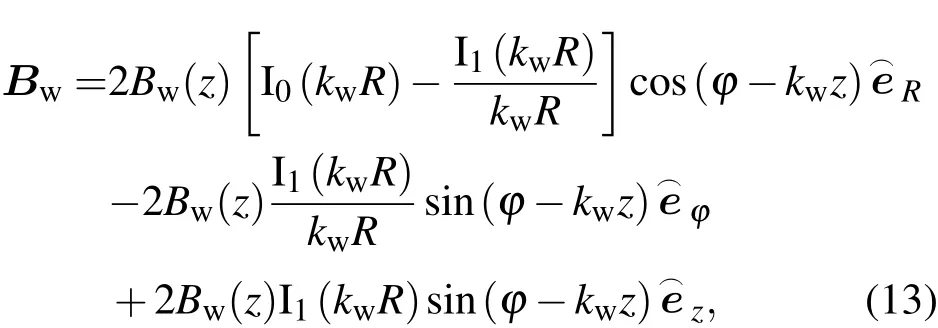
本文充分考虑摇摆器绝热压缩段的影响,其振幅函数为

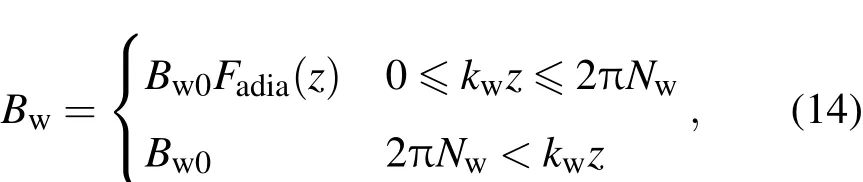
式中Fadia(z)是摇摆器磁场在绝热压缩段0≤kwz≤2πNw内的变化函数,Nw代表绝热压缩周期数目,参数Bw0是摇摆器的幅值,I0(kwR)和I1(kwR)分别为零阶和一阶变型贝塞尔函数.本文以Conde-Bekefi实验[6]为研究对象,故我们用线性拟合方法具体模拟出了该装置所公布的绝热压缩磁场分布曲线(文献[29]图4)：

在数值计算中,本文以摇摆器周期的10-6量级为迭代步长,精细模拟电子在摇摆器中的运动状态.

3 摇摆器绝热压缩磁场对运动稳定性的影响

Conde和Bekefi[6]实验参数为：摇摆器的长度L=200 cm,波长λw=3.18 cm,绝热压缩周期数目Nw=6,电子束的半径Rb=0.2540 cm,相对论能量因子γ=2.4677,流强I=300 A,正向导引磁场B0=4060 G(1 G=10-4T)时摇摆器幅值Bw0=630 G.图1给出有绝热压缩场和无绝热压缩场这两种情况下,初始位置为R0=0.125 cm的测试电子,其k值随迭代次数的演化曲线.从图中可见,在开始阶段,无绝热压缩场的曲线波动较大,但当迭代次数足够大,两者差别越来越小,最后趋向相同k值,即K熵相同.这就表明,在正向导引磁场情况下,摇摆器绝热压缩场对电子的运动稳定性无实质影响.

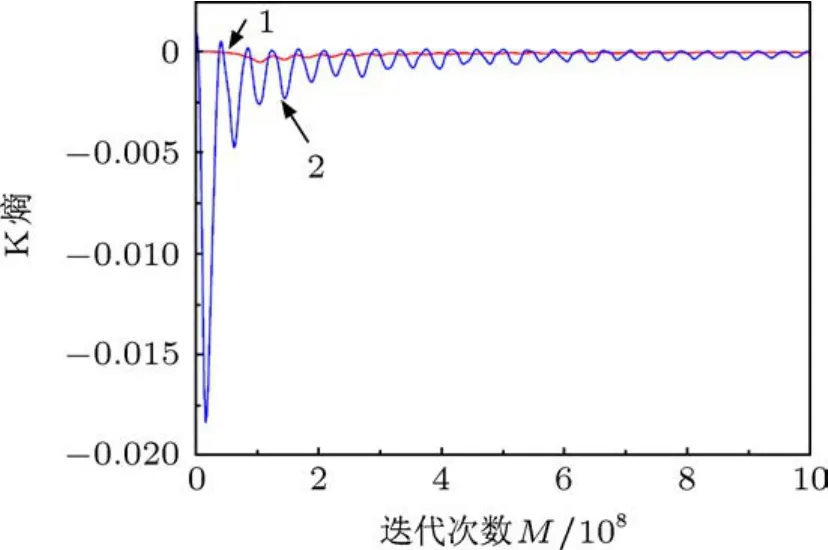
图1 正向导引磁场B0=4060 G,B w0=630 G,摇摆器绝热压缩场对电子运动稳定性K熵的影响 曲线1代表有绝热压缩场,曲线2代表无绝热压缩场

Conde和Bekefi实验采用反向导引磁场B0=-10900 G时,所用的摇摆器磁场幅值Bw0=1470 G[6],相应K熵的曲线演化如图2所示.显而易见,在反向导引磁场情况下,摇摆器绝热压缩场对电子的运动稳定性也无实质影响.

图2 反向导引磁场B0=-10900 G,B w0=1470 G,摇摆器绝热压缩场对电子运动稳定性K熵的影响 曲线1代表有绝热压缩场,曲线2代表无绝热压缩场

应当指出：电子的运动和运动稳定性是不同的概念,从数学上讲,前者对应运动微分方程的解,后者对应该解的稳定性.上面得到的摇摆器绝热压缩场对电子运动稳定性无实质影响结论,并不意味着对电子运动无实质影响.以正向导引磁场情况为例,图3给出了图1对应的电子运动轨迹在横平面的投影,从中可以清楚看到：比起有绝热压缩场情况,无绝热压缩场时电子轨迹散布在宽得多的范围,其瞬时拉莫尔半径要大得多,瞬时导引中心的进动也更严重.这是因为：由于没有绝热压缩磁场,电子进入摇摆器时立刻受到一个较大的洛伦兹力,电子的横向速度迅即陡增,运动出现严重的涨落;而有(15)式所示的绝热压缩磁场时,电子进入摇摆器受到的洛伦兹力由零逐渐增加,其横向速度平缓加大.由此可知,摇摆器绝热压缩场对单电子的运动及整个电子束的成形有实质性影响,它使电子平滑获得横向运动,有利于电子束成形.

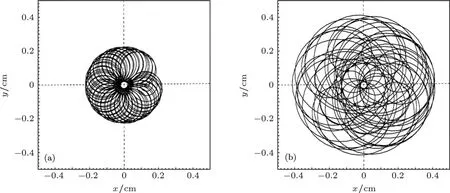
图3 正向导引磁场B0=4060 G,B w0=630 G,摇摆器绝热压缩场对电子运动的影响 (a)和(b)分别代表有绝热压缩场和无绝热压缩场情况下电子轨迹在横平面的投影

4 电子束自身场对运动稳定性的影响

电子束由带负电荷的流动电子组成,因此电子束会在其内部及外部产生如(11),(12)式所表达的自身场,从而置身于自身场中的电子都会受到自身场产生的电场力和磁场力作用.拉曼型自由电子激光器的束流较强,电子束自身场对电子的运动稳定性有着不可忽略的影响.

图4给出对应Conde和Bekefi[6]的正向导引磁场实验参数(B0=4060 G,Bw0=630 G,有绝热压缩磁场)条件下,计入和不计入电子束自身场这两种情况,初始位置为R0=0.125 cm的测试电子,其k值随迭代次数的演化曲线.从图中可见,没有自身场情况下的运动是稳定的(K熵小于零),有自身场情况下的运动是不稳定的(K熵大于零).这就表明,电子束自身场会起到破坏拉曼型正向导引磁场自由电子激光器中电子运动稳定性的负面作用.

但是,对于拉曼型反向导引磁场自由电子激光器,计算结果表明电子束自身场的作用与正向导引磁场中的情况正好相反.对应Conde和Bekefi的反向导引磁场实验参数(B0=-10900 G,Bw0=1470 G,有绝热压缩磁场)[6],图5给出在计入和不计入电子束自身场这两种情况下,初始位置为R0=0.125 cm的测试电子,其k值随迭代次数的演化曲线.从图5中可见,没有自身场情况下的运动是不稳定的(K熵大于零),有自身场情况下的运动是稳定的(K熵小于零).这就表明,电子束自身场有利于拉曼型反向导引磁场自由电子激光器中电子运动稳定性.

图4 正向导引磁场B0=4060 G,B w0=630 G,电子束自身场对电子运动稳定性K熵的影响 曲线1代表无自身场,曲线2代表有自身场

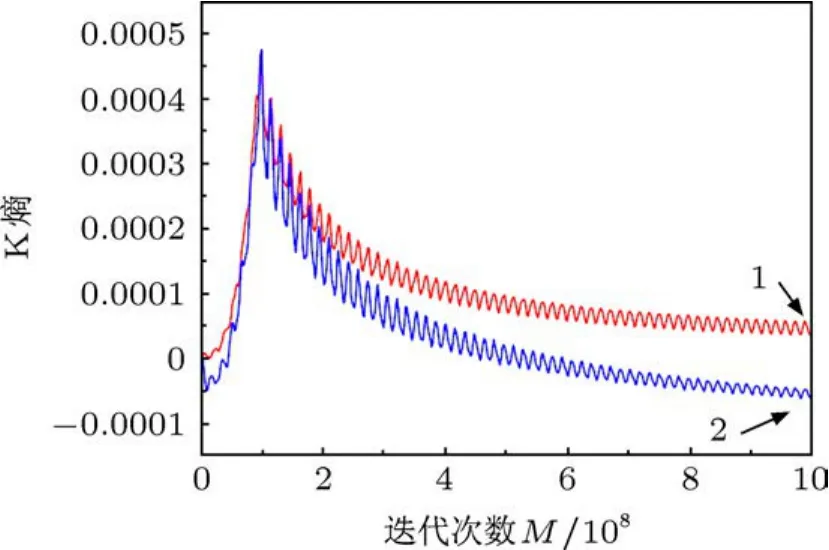
图5 反向导引磁场B0=-10900 G,B w0=1470 G,电子束自身场对电子运动稳定性K熵的影响 曲线1代表无自身场,曲线2代表有自身场

下面探讨产生上述现象的物理原因.从数学物理上讲,微分方程解的稳定性是指解对初始条件的敏感性,为此我们来考察电子进入摇摆器靠近入口处初期阶段的运动状况.众所周知,纵向导引磁场之所以能防止电子运动轨道发散而产生聚束作用,是因为它与电子的横向速度共同产生一个洛伦兹力,该洛伦兹力使电子在横平面做拉莫尔运动,把电子在横平面的运动轨道大致约束在瞬时拉莫尔圆轨道,稳定了电子的运动.如果不考虑电子束自身场,那么横向初始速度为零的电子从纵向射入摇摆器后,其横向速度的获得是由摇摆器的横向磁场与电子的纵向速度共同产生一个横向的洛伦兹力来提供.由于摇摆器绝热压缩段的横向磁场由零逐渐增加到一个恒定幅值Bw0(参见(14),(15)式,其中绝热压缩磁场分布函数一些文献[30]采用解析式,因此电子在摇摆器入口附近的横向速度也由零缓变增加.当考虑电子束自身场,情况就大不同了,会产生一种附加的效应：电子一进入摇摆器就感受到电子束自身产生的径向静电场(参见(11)式),立刻受到径向电场力作用而获得一个横向速度v⊥E,于是纵向导引磁场B0立即与之产生一个横向的洛伦兹力,产生由于自身场附加的拉莫尔运动,其瞬时拉莫尔半径RLE近似关系为;随后,电子在穿越摇摆器绝热压缩区过程中横向速度继续增加,获得增量Δv⊥E(＞0),瞬时拉莫尔半径也对应产生波动量.显然,由于正向导引磁场B0＞0,故ΔRLE＞0,自身场附加的横向位移变化越来越大,起到了削弱电子运动稳定性的作用;而对于反向导引磁场B0＜0,则ΔRLE＜0,自身场附加的横向位移变化越来越小,起到了改善电子运动稳定性的作用.

5 结论

本文以Conde和Bekefi实验数据为例,就摇摆器绝热压缩场和电子束自身场对拉曼型自由电子激光器中相对论电子在正向导引磁场和反向导引磁场两种情况下的运动稳定性做了对比研究.结果表明：1)在正向导引磁场和反向导引磁场两种情况下,摇摆器绝热压缩磁场对电子运动稳定性都无实质性影响,但对电子运动影响大;2)电子束自身场在拉曼型正向导引磁场自由电子激光器中使电子运动稳定性变差,而在拉曼型反向导引磁场自由电子激光器中则可改善电子运动稳定性.

[1]Marshall T C 1985 Free-Electron Lasers(New York：Macmillan Publishing Company)Chaps.1,2,3

[2]Zhang S C 1994 Introduction of Free-Electron Lasers(Chengdu：Southwest Jiaotong University Press)Chaps.1,2,3,6(in Chinese)[张世昌1994自由电子激光导论(成都：西南交通大学出版社)第1,2,3,6章]

[3]Emma P,Akre R,Arthur J,Binota R,Bostedt C 2012 Nature Photonics 4 641

[4]Tersuya H 2011 Synchrotron Radiation News24 20

[5]Orzechowski T,Anderson B,Clark J,Fawley W,Pau A,Prosnitz D,Scharlemann E,Yarema S 1986 Phys.Rev.Lett.57 2172

[6]Conde M,Bekefi G 1991 Phys.Rev.Lett.67 3082

[7]Xie J,Zhuang J,Huang Y,Li Y,Lin S,Yang R,Zhong Y,Zhang L,Wu G,Zhang Y,Chao C,Li L,Fu E,Su J,Wang Y,Wang G 1995 Nucl.Instru.Meth.Phys.Res.A358 256

[8]Jin X,Li M,Xu Z,Li W,Yang X 2006 High Energy Phys.&Nucl.Phys.30 96(in Chinese)[金晓,黎明,许州,黎维华,杨兴繁2006高能物理与核物理30 96]

[9]Dai J,Deng H,Dai Z 2012 Phys.Rev.Lett.108 034802

[10]Labat M,Bellaveglia M,Bougeard M,Carre B,Ciocci F 2011 Phys.Rev.Lett.107 224801

[11]Son S,Moon S 2012 Phys.Plasmas19 063102

[12]Zhang SC 2010 Phys.Plasmas17 053102

[13]Lin X,Zhang J,Lu Y,Luo F,Lu S,Yu T,Dai Z 2010 Chin Phys.Lett.27 044101

[14]Kong Y Y,Zhang SC 2011 Acta Phys.Sin.60 095201(in Chinese)[孔艳岩,张世昌2011物理学报60 095201]

[15]Ginzburg N,Golubev I,Kaminsky A,Kuzikov S,Perelstein E 2011 Phys.Rev.STAccel.Beams14 041002

[16]Vikharev A,Ginzburg N,Golubev I,Danilov Y,Zaitsev N 2011 Tech.Phys.Lett.37 102

[17]Chen C,Davidson RC 1990 Phys.Fluids B 2 171

[18]Chen C,Davidson RC 1990 Phys.Rev.A 42 5041

[19]Spindler G,Renz G 1991 Phys.Fluids B 3 3517

[20]Zhang SC,Xu Y,Liu QX 1993 Phys.Rev.E 48 3952

[21]Zhang SC,Xu Y 1993 Phys.Lett.A 179 311

[22]Nasr N,Mehdian H,Hasanbeigi A 2011 Phys.Plasmas18 043104

[23]Abarbanel H,Brown R,Sidorovich J,Tsimring L 1993 Rev.Mod.Phys.65 1331

[24]Benettin G,Galgani L,Strelcyn J1976 Phys.Rev.A 14 2338

[25]Zhang SC,Liu Q X,Xu Y 1994 Acta Phys.Sin.43 225(in Chinese)[张世昌,刘庆想,徐勇1994物理学报43 225]

[26]Zhang SC,Elgin J2004 Phys.Plasmas11 1663

[27]Taghavi A,Esmaeilzadeh M,Fallah M 2010Phys.Plasmas17093103

[28]Zhang SC 2013 Phys.Lett.A 377 319

[29]Fajans J,Bekefi G,Yin Y Z 1985 Phys.Fluids28 1995

[30]Freund H,Ganguly A 1986 Phys.Rev.A 33 1060