硅团簇自旋电子器件的理论研究*

黄耀清 郝成红† 郑继明 任兆玉‡

1)(上海应用技术学院理学院,上海 201418)

2)(西北大学光子学与光子技术研究所,西安 710069)

(2012年11月28日收到;2012年12月23日收到修改稿)

1 引言

随着电子器件向更快、更冷、更小的方向不断地朝高端发展,传统集成电路必将进入介观领域,更小的器件尺寸、更高的加工精度以及基于量子规律的设计理论,都对传统半导体技术提出了极大的挑战,同时也促使人们去构建全新一代的电子器件.为此,有两个探索方向得到了极大关注：其一是基于介观系统的电子弹道输运行为,利用分子(包括团簇)来实现整流、放大等最基本的数字电路功能,实现所谓的分子电子器件[1-5];其二是把电子的自旋也作为信息载体,利用自旋弛豫时间长,易于通过外磁场调节等优点,实现所谓的自旋电子器件[6-10].现阶段,不论是分子器件还是自旋器件,通向实用化最重要的难关之一就是可控制备.不可控的分子结细节变化,使得分子导电性质的测量数据面临稳定性与再现性的考验[3-5],限制了此类器件进入实际应用领域.

为了同时满足性能可控和制备可控性,作为中心散射区的团簇或分子应具备两个重要的特性：一是在形成分子结时能保持几何结构的稳定性;另外一个是可以通过简单的方式有效地改变或调控分子结的物理性能.除了有机分子之外,过渡金属掺杂的硅团簇也以其潜在的性能可设计性,成为构建分子自旋器件的主要候选对象[11-13].文献[14—16]研究表明：几乎所有的由12个硅原子围绕过渡金属组成的六棱柱笼状结构表现出了较好的几何结构稳定性.由于实验手段的限制,测量单个团簇的输运性质仍然十分困难.Desmicht等[17]提出了用一种实验方法来测量单个Co纳米颗粒的输运行为;Sordan等[18],Bernand等[19]也分别报道了有关单个纳米颗粒电子输运的研究结果,发现了库仑阻塞效应和自旋注入现象.这些研究充分表明由团簇来构建纳米电子器件的有效性.但是,上述的研究结果都是针对金属团簇研究得到的,而且团簇的尺寸一般都在几个纳米以上,目前尚缺少对更小尺寸的团簇以及硅基团簇电子输运性质的实验研究.而这种缺失正是模拟研究作为先导可以弥补的[20,21].

我们设想通过掺杂不同的过渡金属到具有稳定性的Si12团簇中,既可以保证团簇的稳定性,又可以有效地调控团簇的磁性等物理性能,从而可以达到作为中心散射区的团簇或分子应满足的性能可控和制备可控的要求.因此,本文选取了一系列3d过渡金属(TM)掺杂的Si12六棱柱笼状结构团簇,通过调整掺杂的过渡金属元素,以期达到有效控制团簇电子结构,尤其是电子自旋布局的目的,以进一步考察这些团簇的电子自旋极化输运性质.

2 计算细节

采用如图1所示的模拟模型,Si12TM团簇位于两段半无限长的Au(111)-(3×3)的电极之间,组成了金属-分子-金属双探针系统(the two-probe system).利用基于非平衡格林函数(NEGF)和密度泛函理论(DFT)的介观体系电子输运性质模拟软件包Nanodcal[22,23],对系统的自旋极化输运性质进行了模拟.目前,利用这一软件研究自旋相关问题的报道已经有很多,例如文献[24,25],充分说明这一算法在自旋输运模拟上的可行性是有保证和得到广泛认可的.

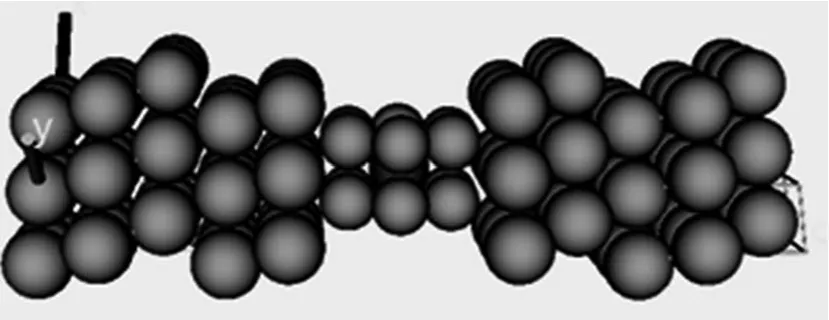
图1 Au/Si12TM/Au分子结模型示意图

介观尺度下的电子输运呈现出弹道式的输运方式,即电子通过分子结时,不会受到来自声子和杂质的散射,具有相位相干性.此时,决定其电流大小的因素不仅有电压,还有分子和电极的耦合强弱.在实际计算中,双探针系统常被分为三部分：左、右半无限长的电极和中心团簇加部分左、右电极共同组成的中心散射区.中心散射区包括半无限长电极的一部分,用以屏蔽中间原子尺度导体对电极势的影响,从而让中间导体近似的处于块体势之中.通过中心区导体的电流可以根据如下Landauer-Bu¨ttiker公式积分得到：

其中ul和ur分别为左右电极的化学势,fl,fr分别为两个电极的电子分布函数,而T(E,V)是在偏压为V,能量为E时的透射系数.

在整个DFT计算中,采用了局域密度近似,交换关联泛函为Perdew和Zunger[26]所提出的参数化泛函(LDAPZ81),所有原子的基组为双ζ加极化(DZP)基组,截断能取150 Ry.在Si12TM团簇左侧硅原子与左电极的距离dAu-Si约为0.23 nm时,对分子结的几何构型进行优化(使得每个原子受力小于0.5 eV/nm)后,系统研究了Au/Si12TM/Au系统的自旋极化的电子输运特性.

3 结果与讨论

3.1 Si12Fe团簇平衡态透射谱

当团簇被放置在相距非常近的两电极之间形成金属-团簇-金属的双探针系统时,其电子结构也会由于团簇-电极耦合的存在而受到影响.团簇的部分电子态扩展到了电极中,同时电极的部分电子态也扩展进了团簇中[27].团簇的电子态起到了联通两边电极电子库的作用.特定能量态的电极电子以一定的概率通过团簇而进入另一电极;同时,分子结中的局域电子又会散射通过分子结的具有相同自旋的传导电子,从而使得流过分子结的电流具有自旋极化的特性,通过对透射谱和态密度(DOS)的分析,可以获得电子通过金属-团簇-金属结的详细输运信息.

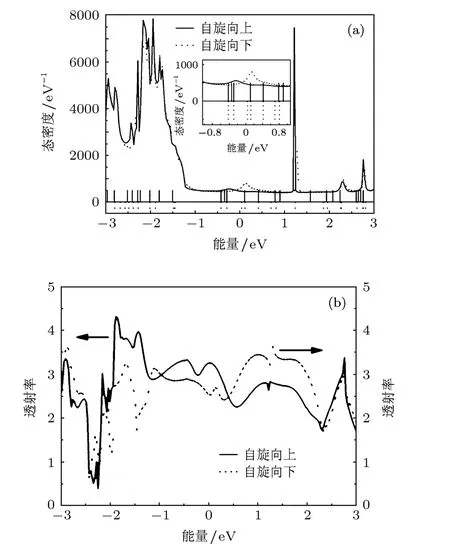
图2 Au/Si12Fe/Au系统的(a)DOS,(b)平衡态透射谱

图2是计算得到的Au/Si12Fe/Au系统的平衡态透射谱和DOS.从图2中可以看出：系统的DOS只在-1.2—1.5 eV范围有较大的极化,小于-1.2 eV后,DOS峰尽管较高,但两个自旋态的DOS基本重合(本文中费米能级均被设定为能量零点).我们以前的研究表明：金纳米线的电子态主要集中在能量小于-1.5 eV以下的范围内,而-1.5—3.0 eV范围内的电极电子态较少[28].对比图2(a)可以发现：能量小于-1.2 eV后DOS的主要来源就是这些未极化的金导线的电子态;而能量在-1.2—3.0 eV范围时,DOS应当来源于自旋极化的团簇电子态.

在透射谱中(图2(b)),费米能级附近的自旋极化现象十分明显,在0.5—2.2 eV范围,自旋向上电子的透射率明显低于自旋向下电子的透射率,而在-2—0.5 eV范围内,自旋向上电子的透射率明显高于自旋向下电子的透射率.自旋极化透射率的大小,主要受两方面因素的控制,其一是团簇-电极电子态的耦合强弱,它决定了透射率的大小;其二是当不同自旋的团簇电子态与电极电子态具有相同态耦合强度时,局域自旋对同自旋电子的散射强弱决定了自旋极化的程度.因此,可把极化透射谱按控制因素不同而分为两个部分.

第一部分位于-1.1—0.5 eV范围,此时电极电子态较少,不同自旋的团簇电子态与电极态的耦合强弱相当.局域自旋对同自旋电子的散射强弱不同,是传导电子极化透射的控制因素.如图2(a)所示,DOS谱中自旋向上(-0.23 eV附近)和自旋向下(0.14 eV附近)的部分都存在相似的宽峰,表明这些能量位置附近存在大量非局域的团簇电子态,它们将与电极电子态在这里发生较强的耦合,从而提供有效地“通道”联接起左、右电极中的同自旋电子,导致了较高的透射率.而从过渡金属原子的电子占据情况分析,如表1中投影到铁原子上的分子自洽哈密顿量(MPSH)发现：-3—3 eV的能量范围内,铁原子的自旋向上的能级主要分布在-1 eV以下,而相应铁原子的自旋向下的能级都集中在-0.7—0.14 eV这一能量范围.铁原子的3d电子是定域性强的价电子,这种电子将强烈地散射同自旋的传导电子,使得透射率降低[13],故而可以看到-1.1—0.5 eV内自旋向上电子的透射率要大于自旋向下的电子的透射率.

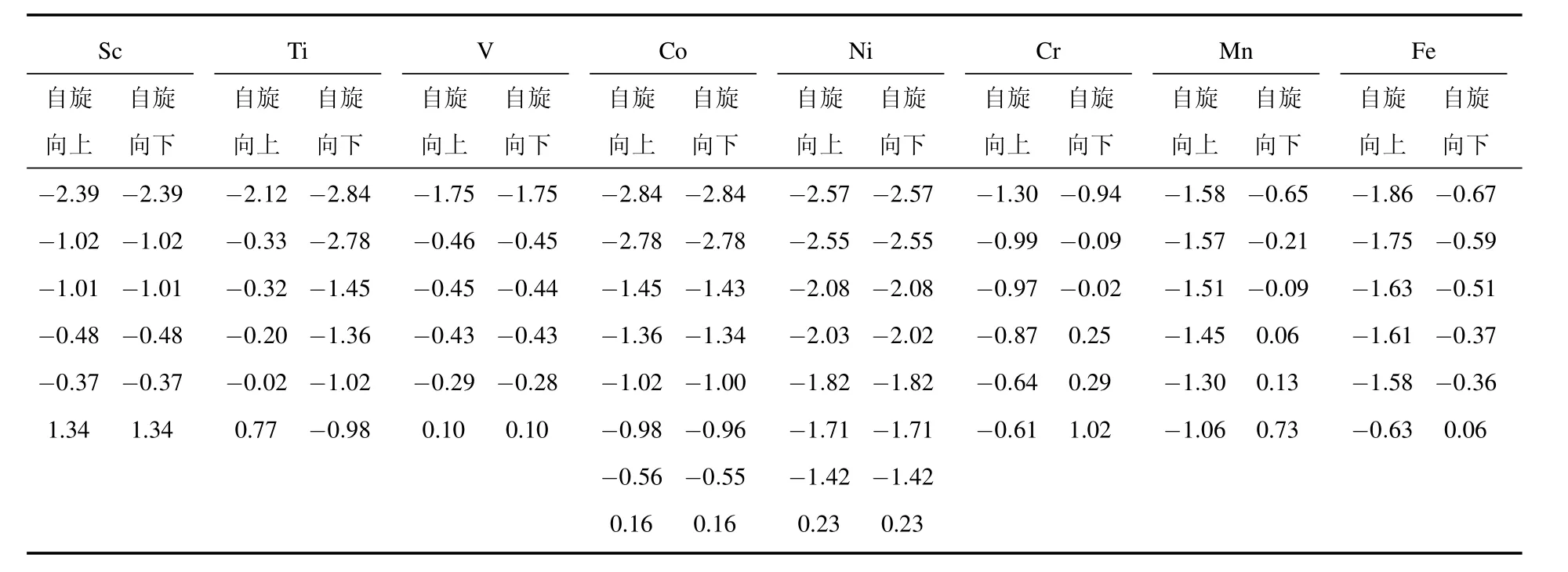
表1 投影到各过渡金属原子上的MPSH的能量位置(单位：eV)

第二部分在-2—-1.1 eV和0.5—2.2 eV范围.此时,同一能量范围内的团簇-电极耦合,对于不同自旋态有较大地强弱差别,成为传导电子极化透射率的主要控制因素.图3给出了投影到团簇上的MPSH轨道图,其中各能级的能量位置显示在图2(a)中.从图3中可以明显地看出,自旋向上和向下的团簇能级在-2.01—-1.0 eV范围分别有4条.其中自旋向上的最高占据轨道(HOMO-6,HOMO-5)明显地具有较大的“尾巴”,可以与电极电子态产生强耦合,从而导致高的透射率;而与同在这一能量范围内自旋向上的轨道相比,除了自旋向下的HOMO-4外,其他所有自旋向下的电子轨道主要集中在团簇内,与电极的耦合较弱,这势必导致该能量范围类自旋向上的透射强于自旋向下的透射.按照之前的分析,投影到铁原子的自旋向上的MPSH位置主要在-2.01—-1.0 eV这一能量范围,故而自旋向上的传导电子应该在这一能量范围内受到更大的散射,但在图2(b)中该范围内的自旋向上的透射峰值却并未低于自旋向下的透射峰值;说明团簇-电极耦合强度对透射谱的影响要大于局域自旋散射作用对透射谱的影响.

从图3还可以发现：Si12Fe的自旋向上的MPSH中HOMO和最低未被占据轨道(LUMO)均来自铁原子d电子的贡献,而其HMOM-2则明显具有硅原子的s,p电子的特征.该能级位于-0.42 eV处,对应于图2(a)中-0.23 eV处的自旋向上的总态密度峰.同样的,自旋向下的HOMO-1具有与自旋向上HMOM-2轨道相似的来源,但却没有自旋向下的总态密度峰与之对应.这应该归因于这一能量范围内自旋向下的局域d电子对同自旋传导电子的排斥,增大了自旋向下电子的能量,使得总自旋向下的态密度峰上移至0.14 eV处.

至此,以上的分析表明,在费米能级附近,不同自旋的团簇电子态与电极电子态耦合强弱相似,而极化占据的Fe原子的局域3d电子在这一能量范围内主要出现的是自旋向下的部分,这些电子将强烈地散射同自旋的传导电子,导致自旋向下的透射较低.尽管Fe原子自旋向上的电子数更多,但是它们的能量位置比自旋向下的电子能级更远离费米能级,使得在费米能级附近出现了自旋向上电子透射率大于自旋向下电子透射率的极化输运性质.

3.2 不同掺杂对输运性质的影响

以上的讨论可以看出,团簇-电极耦合和团簇本身的局域电子共同作用将决定整个系统的极化输运性质.我们设想通过调节团簇中掺杂的过渡金属原子来达到控制局域自旋数目,进而控制系统极化输运性质的目的.表2是各种3d过渡金属掺杂后的自旋过滤效率(SFE)和该团簇中过渡金属的Mulliken布居.其中SFE定义如下

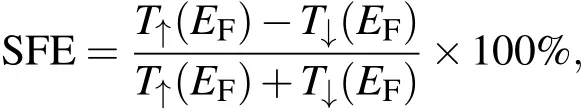
T↑(EF)和T↓(EF)分别代表费米能级(EF)处的自旋向上和自旋向下的透射系数.

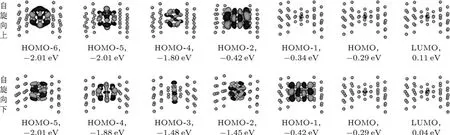
图3 投影到Si12 Fe团簇上的各个MPSH的等值面图,其能量位置标注在各图下;为了显示出团簇在分子结中的相对位置,每张图中两端的原子面代表金电极

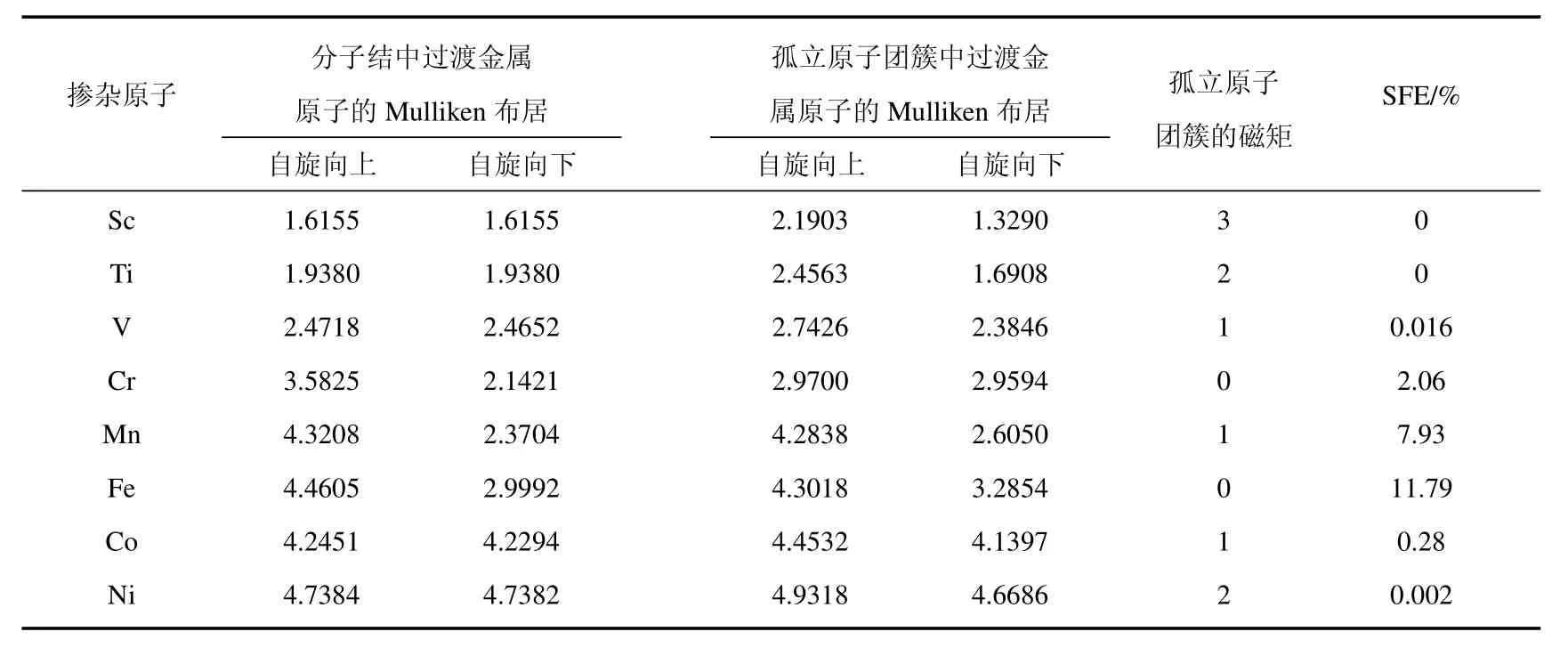
表2 过渡金属原子在孤立团簇和分子结中的Mulliken布居对比和系统的SFE

从表2中发现,在铁磁性金属Fe,Co和Ni掺杂的体系中只有Fe掺杂的体系呈现出较明显的自旋极化透射现象,Co,Ni以及V掺杂的体系只有微弱的自旋极化的透射;但是在非磁性金属Cr和Mn掺杂的体系中竟然又出现了较明显的自旋极化透射现象.从Sc到Ni的掺杂,体系的自旋极化透射能力先增大后迅速减小,在Fe掺杂的系统中出现最大值.

图4给出了计算得到的不同掺杂体系的透射谱(部分结果).图4(a),(d)和(e)所示为Sc,Co和Ni掺杂体系的透射谱,与此相似的Ti和V掺杂的结果没有给出(为了更清晰地表达出自旋向上的透射与自旋向下的透射率完全一致,图中用了双Y坐标,左边的比右边的Y轴略有提高,以使两条完全一样的曲线分开显示).图4(b)和(c)是Cr和Mn掺杂体系的透射谱,这两幅图以及图2(b)(Fe掺杂体系的透射谱)也采用了双Y坐标,但是左、右Y轴的零基准一致.从这些图中可以明显地看到不同自旋电子的透射在费米能级附近发生了较大的极化,极化程度按Cr,Mn和Fe掺杂的顺序依次增强.

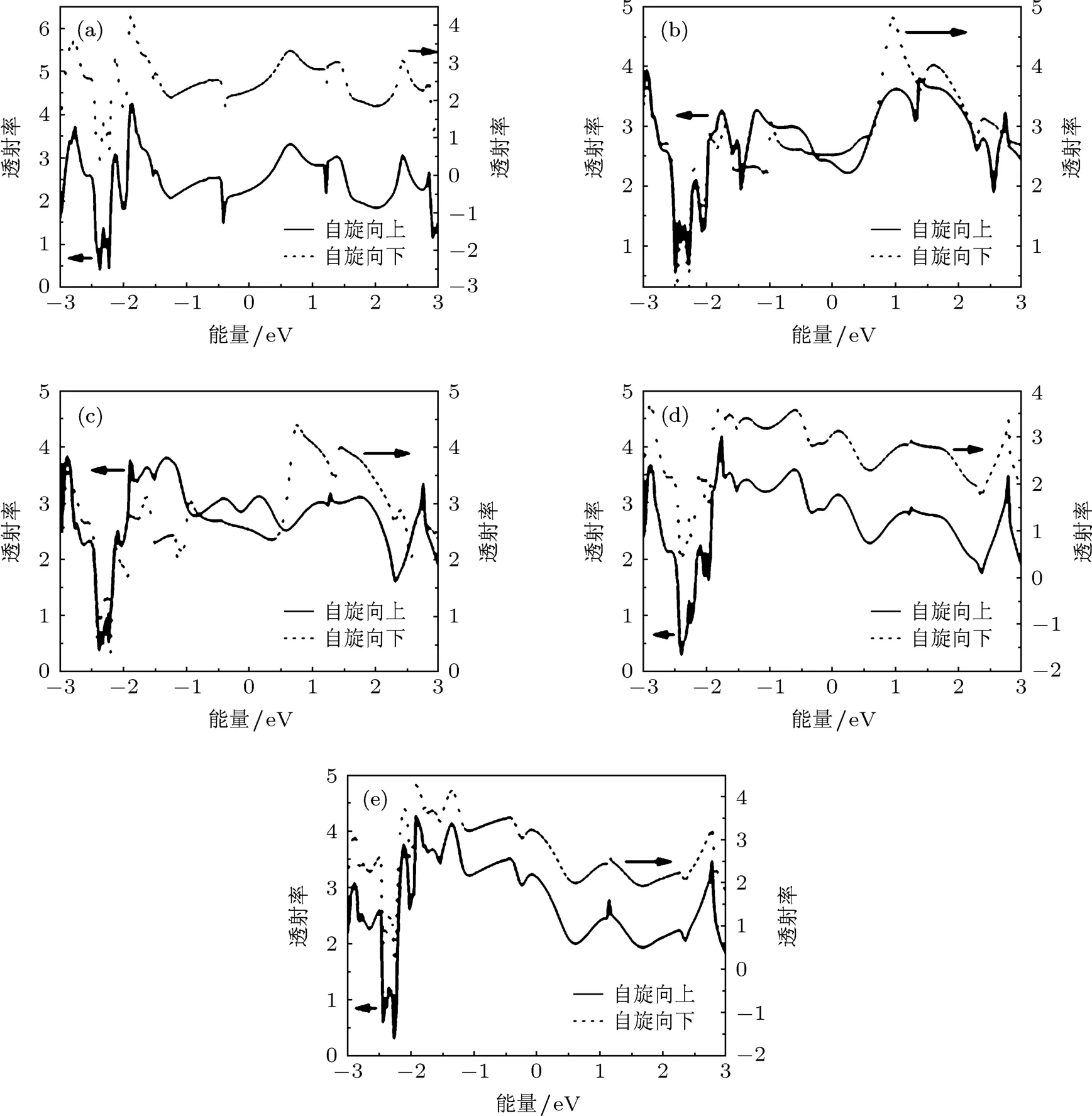
图4 Au/Si12TM/Au系统的平衡态透射谱 (a)Au/Si12Sc/Au;(b)Au/Si12Cr/Au;(c)Au/Si12Mn/Au;(d)Au/Si12Co/Au;(e)Au/Si12Ni/Au

作为对比,我们计算了3d过渡金属掺杂的孤立Si12TM团簇的磁矩,发现(表2)从Sc到Ni的掺杂,团簇的磁矩具有与孤立过渡金属原子磁矩完全不同的变化趋势,Sc掺杂在的Si12Sc团簇具有3µB磁矩,Si12Ti团簇次之,具有2µB磁矩,从Si12V团簇到Si12Co团簇,1µB磁矩和磁性完全猝灭的情况交替出现,取决于团簇的电子数的奇偶性,奇数个电子的团簇有1µB磁矩,偶数个电子的磁性完全猝灭,直到Si12Ni团簇又出现了2µB磁矩.过渡金属掺杂的硅团簇的磁性变化已经有过较深入的研究,发现这类型的团簇的磁性变化具有丰富的形式,与众多的因素有关,例如掺杂原子的类型、团簇的几何构型,硅原子数、p-d电子杂化等等.Khanna等[14]研究指出,Si12Cr团簇磁性完全猝灭的原因是由于p-d电子杂化,过渡金属的3d电子和4p空轨道都对团簇的前线轨道有较大贡献,使得电子对团簇的分子轨道的占据发生了不同于孤立电子过渡金属原子的情况.

最近,Reveles等[29]的研究指出：只有同属于价层空间的过渡金属的d电子与配体的价电子轨道分裂成为两个独立的子空间时,团簇的磁矩才会按照孤立原子磁矩变化.我们最初的设想,即只依靠掺杂不同过渡金属而完全调控团簇磁性的方法,只有在这种条件下才完全适用,因此对于硅团簇磁性控制还有待更细致的理论研究.而且,我们的计算还表明,分子结的自旋极化输运能力与团簇孤立状态下的磁矩也无一致性.例如,我们发现非磁性金属Cr掺杂,在孤立团簇状态下磁性猝灭,但是在形成分子结时却出现了自旋极化的现象.对这种现象产生的原因,我们分析后认为,分子结中的团簇受到来自电极的微扰,使得它本身的势场对称性发生一定的变化;同时,扩展到分子结中的电极电子态必然使得团簇的电子占据情况发生变化.Mulliken布居分析(表2)表明,孤立原子团簇的Mulliken布居总和小于分子结中的团簇的Mulliken布居总和,分子结中的团簇得到了电极近一个电子,而且这多出来的近一个电子有较大的几率分布在过渡金属轨道占主要成分的团簇轨道上.沿着Reveles等[29]的研究思路,我们认为同在价层空间里的局域的过渡金属d轨道和非局域的硅原子s,p轨道,尽管没有严格的分裂成两个独立的子空间,但是随掺杂原子的变化,两者的能量间距发生了变化;在Sc到V的掺杂体系,d轨道位置与硅原子s,p轨道能量差别小,局域和非局域的原子轨道杂化强,从电极进入团簇的电子倾向于占据这种未成对的团簇轨道,进而分子结中没有未成对电子存在,使通过分子结的电流没有自旋极化行为出现.但是,在Cr,Mn和Fe掺杂的体系中,d轨道位置与硅原子s,p轨道能量差增大,杂化减小,从电极进入团簇的电子与硅原子s,p电子就已经满足了形成稳定壳层所需的电子数,则较低能量的d电子将会向原子状态的电子占据回归,进而分子结中出现未成对电子,使通过分子结的电流出现自旋极化行为出现,并在Fe掺杂系统达到最强.最后,在Co和Ni掺杂的体系中,尽管d轨道位置与硅原子s,p轨道能量差继续增大,但由于过渡金属本身的电子数增加,再加上从电极进入团簇的电子,使得d电子轨道被满占据,进而分子结中没有未成对电子存在,使通过分子结的电流再次回归到没有自旋极化的状态.

4 结论

利用密度泛函和非平衡格林函数方法,系统地研究了过渡金属掺杂的Si12TM团簇的电子自旋极化输运性质.考察了孤立硅原子团簇的磁性受到掺杂过渡金属性质的影响,发现孤立团簇的磁矩与所掺杂原子的磁矩无一致性;且当团簇放置到金电极之间后,分子结的自旋极化输运能力与团簇孤立状态下的磁矩也无一致性.通过分析系统态密度、透射谱与分别投影到团簇和过渡金属的MPSH的关系,发现电极电子态与团簇电子态的耦合强弱主要决定了系统的透射能力,在具有相同耦合强度的条件下,局域电子的分布决定了电子输运的自旋极化程度.在铁磁性金属Fe,Co和Ni掺杂的体系中只有Fe掺杂的体系呈现出较明显的自旋极化透射现象,Co,Ni和V掺杂的体系只有微弱的自旋极化的透射;但是在非磁性金属Cr和Mn掺杂的体系中竟然又出现了较明显的自旋极化透射现象.从Sc到Ni的掺杂,体系的自旋极化透射能力先增大后迅速减小,在Fe掺杂的系统中出现最大值.

[1]Reed M A,Zhou C 1997 Science 278 252

[2]Venkataraman L,Klare JE 2006 Nature 442 904

[3]Quinn JR,Foss FW 2007 J.Am.Chem.Soc.129 6714

[4]Venkataraman L,Klare JE 2006 Nano Lett.6 458

[5]Dadosh T,Gordin Y 2005 Nature 436 677

[6]IgorˇZ,Jaroslav F,Sarma SD 2004 Rev.Mod.Phys.76 323

[7]Xiong Z H,Wu D,Vardeny Z V,Shi J2004 Nature427 821

[8]Rocha A R,V´ıctor M G,Steve WB,Colin JL,Jaime F,Stefano S2005 Nat.Mater.4 335

[9]Salvador B L,Mihajlo V,Markus K,Chou M Y 2010 Phys.Rev.Lett.104 076807

[10]Petta JR,Slater SK,Ralph D C 2004 Phys.Rev.Lett.96 136601.

[11]Zheng X L,Zheng JM,Ren Z Y,Guo P,Tian JS,Bai JT 2009 Acta Phys.Sin.58 5709(in Chinese)[郑新亮,郑继明,任兆玉,郭平,田进寿,白晋涛2009物理学报58 5709]

[12]Dai Z X,Zheng X H,Shi X Q,Zeng Z 2005 Phys.Rev.B 72 205408

[13]Ling ZK,James RC 2008 Phys.Rev.B 77 073401

[14]Khanna SN,Rao B K,Jena P 2002 Phys.Rev.Lett.89 016803

[15]Hagelberg F,Xiao C,William Jr A L 2003 Phys.Rev.B 67 035426

[16]Hidefumi H,Takehide M,Toshihiko K 2001 Phys.Rev.Lett.86 1733

[17]Desmicht R,Faini G,Cros,V,Fert A,Petroff F,Vaure‘s A 1998 Appl.Phys.Lett.72 386

[18]Sordan R,Balasubramanian K,Burghard M,Kern K 2005 Appl.Phys.Lett.87 013106

[19]Bernand M A,Seneor P,Lidgi N,Mun˜oz M,Cros V,Fusil S,Bouzehouane K,Deranlot C,Vaures A,Petroff F,Fert A 2006 Appl.Phys.Lett.89 062502

[20]Chen H 2007 Physics36 910(in Chinese)[陈灏2007物理36 910]

[21]Han RS2010 Physics39 753(in Chinese)[韩汝珊2010物理39 753]

[22]Taylor J,Guo H,Wang J2001 Phys.Rev.B 63 245407

[23]http：//www.nanoacademic.ca[2012-10-20]

[24]Zhao Y,Hu Y,Liu L,Zhu Y,Hong G 2011 Nano Lett.11 2088

[25]Bin W,Jian W 2011 Phys.Rev.B 84 165401

[26]Perdew JP,Zunger A 1981 Phys.Rev.B 23 5048

[27]Datta S 2005 Quantum Transport：Atom to Transistor(Cambridge：Cambridge University Press)

[28]Zheng JM 2008 Ph.D.Dissertation(Xian：Northwest University)(in Chinese)[郑继明2008博士学位论文(西安：西北大学)]

[29]Reveles JU,Clayborne PA,Reber A C,Khanna SN,Pradhan K,Sen P,Pederson M R 2009 Nat.Chem.1 310