高速磨削楔形区气流场建模与仿真*

韩振鲁 李长河 王 胜 张 强

(青岛理工大学机械工程学院，山东青岛 266033)

高速磨削加工中，主轴带动砂轮一起旋转，旋转运动会对周围的空气流场产生扰动，在旋转砂轮的周边存在着一个空气附面层，阻碍磨削液向射流区和磨削区的供给，通常将其称为“气障”。砂轮旋转速度越高，空气流的“气障”越大，磨削液就越难被供给到磨削区［1］。在平面磨削加工中，工件与砂轮之间具有一定的楔形间隙，砂轮的高速旋转带动周围空气流动，除在砂轮周围形成一定厚度的气障层外，在靠近工件表面还会出现一定程度的返回流［2］。本文主要对楔形区气流场和返回流进行理论建模与仿真研究。

1 砂轮表面气障分析

1.1 气障的形成

在高速回转的砂轮表面一般存在有4种回转气流，圆周环流、浸透流、内部流及径向流。这是由于砂轮表面与空气的摩擦以及离心力作用造成的。对于金属基体的CBN砂轮，因为金属基体中没有气孔存在，所以就不存在内部流及浸透流，而只有圆周环流、径向流。圆周环流就是绕着砂轮周向旋转的气流，对磨削液的供给有阻碍作用。径向流是由于砂轮端面同空气的相互作用和离心力共同形成的，它对冷却液的供给影响不大［3］。

1904年普朗特对此提出了一个突破性的看法:附面层理论。它认识到虽然所有的实际流体都是有粘性的，但在流动中粘性力的重要性并不是到处一样的，离开物体表面很远的地方粘性力基本上不起作用，只在物面附近一层很薄的流体(称附面层)内，粘性力才是必须考虑的。这样就可以把整个流动分成两部分来处理:远离物面的部分可以用无粘性的理论做计算，而贴近物面的一层流体的流动需要做粘流分析。这个概念将粘流计算限制在薄薄的附面层内，使纳维斯托克斯方程可以大大地简化，砂轮周围气流场问题能得到解答［4］。

1.2 平面磨削楔形区气流场理论建模

在高速平面磨削楔形区二维气流场分析计算中采用有限元分析计算方法，建立楔形区二维气流场数学模型，合理确定其边界条件，进行楔形区气流场有限元计算求解，并分析气流场的影响因素。物理模型如图1所示，建立二维坐标系，其中坐标原点位于砂轮与工件最小间隙处的工件表面上。

根据流体力学理论对于粘性流体的流动，流函数Ψ和势函数Φ均满足拉布拉斯(Laplace)方程［5］:

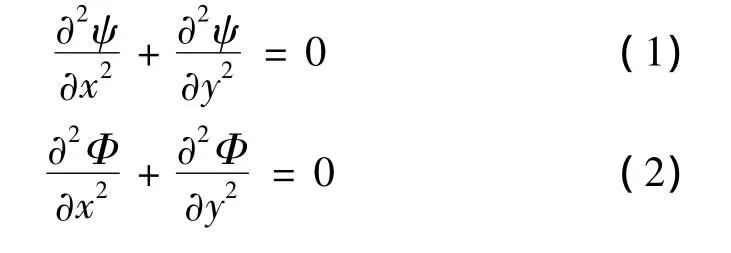
流函数方程对应的边界条件:在第一类边界条件Г1上，满足迪里西来(Dirichlet)条件:

在第二类边界条件Г2上满足诺依曼(Nuemann)条件，即:

势函数方程对应的边界条件:

第一类边界条件Г1上，满足迪里西来条件，即:

第二类边界条件Г2上满足诺依曼条件，即:

求解问题时，须根据求解问题选择使用流函数方程相应的边界条件，或者是势函数方程及相应的边界条件。

由偏微分的数学定义，拉普拉斯型流函数方程对应的泛函表达式为:

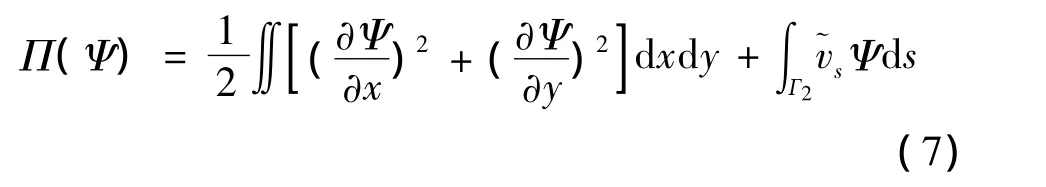
其极值的必要条件是泛函数的一阶变分δΠ=0，由此得:

由迦辽金加权余量法方程(3)可以改成:

应用格林公式，上式变换为:

式(8)和(10)具有相同的形式。

应用于平面粘性流体流动的连续性方程和运动方程为:

应用涡量和流函数定义:

并将两个定义式代入式12～13得:

这就是流函数和涡量方程。式(16)是椭圆型泊松方程，称为流函数方程;式(17)是拟线型抛物线型方程，称为涡量传输方程。式中(∂Ψ/∂y)(∂Ω/∂x)－(∂Ψ/∂x)(∂Ω/∂y)是非线性对流项，γ(∂2Ω/∂x2+ ∂2Ω/∂y2)是粘性扩散项。

应用迦辽金法可写出流函数方程(16)和涡量方程(17)的迦辽金表达式为:

应用格林公式，进行数学运算，式(18)可以改写成:

由构造的流函数和涡量的差值函数及其变分关系式，可得流函数的矩阵表达式:

式中:¯r= ∂Ψ/∂n为自然边界条件的值;φi为流函数 Ψ的插值函数为涡量Ω的插值函数。

在全流域对方程式(21)进行总体合成的总体方程:

引入所需边界条件后，可采用交叉迭代法求解，求出全流场各节点的流函数值。

2 平面磨削楔形区气流场仿真

2.1 平面磨削楔形区气流场仿真结果

本文仿真条件下砂轮以45 m/s的线速度顺时针旋转，因此设定砂轮与工件楔形区右端为楔形区入口区域，左端为楔形区出口区域。为简化计算，现对模型进行以下简化:

(1)由于气流场中气体粘度较低，因此忽略温度和压力对流体粘度的影响，而且不考虑其流动中的惯性效应;

(2)不考虑工件表面粗糙度的影响及弹性变形;

(3)工件的进给速度与砂轮转速相比忽略不计。

从图2、3可以看出，平面磨削流场中在砂轮表面存在明显的气障层，而且由于工件的存在，在砂轮与工件之间的楔形区内空气的速度呈现一定的规律，并且在楔形区入口处出现了“返回流”。在楔形区入口处压力较大，而在靠近最小间隙处的楔形区出口处出现了一定程度的负压。

在砂轮与工件楔形区入口的前端出现了回流现象，说明磨削区附近的工件表面会有反向气流。图3为楔形区局部放大速度矢量图，其箭头方向代表了速度方向，在边界线的上方，空气流动速度方向与砂轮旋转线速度同向，其水平方向的速度是由楔形区入口指向出口，该速度有助于磨削液进入砂轮与工件的楔形间隙;而在边界线的下方，空气流动速度方向与砂轮旋转线速度反向，其水平方向的速度是由楔形区出口指向入口，该速度不利于磨削液进入砂轮与工件的楔形间隙。喷嘴向楔形区喷射入磨削液时，应尽量在边界线的上方射入，这样有助于磨削液进入砂轮与工件的楔形间隙。相关研究已经表明，当喷嘴轴线与工件表面呈一定角度(15°～20°)时，磨削液比较容易进入楔形间隙［6］。

2.2 平面磨削楔形区气流场返回流的分布

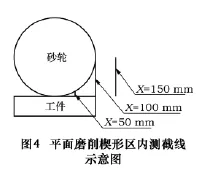
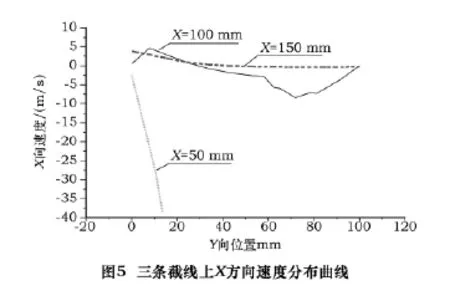
为定量研究平面磨削楔形区内返回流出现的位置，图4给出了磨削流场楔形区内距离最小间隙不同距离的3个测量截线的示意图。3条线距最小间隙处的距离分别为 50 mm，100 mm和150 mm。图5为该3条截线上水平方向的速度分布曲线。

在x=50 mm处的截线上的所有节点其x方向速度均为负值，即速度方向与x轴正方向相反，表明气流方向由楔形区入口指向出口，不存在反向气流;而在x=100 mm处的截线上，在y向坐标为0～27 mm之间的节点，其x方向速度均为正值，速度方向与x轴正方向相同，表明气流方向由楔形区出口指向入口，即存在反向气流会阻碍磨削液进入楔形区，其中极点坐标为(100，12)，说明在该节点处反向气流最剧烈;而在x=150 mm处的截线上，其所有节点的x方向速度均为正值，但由于距离楔形区距离较远，所以其气流方向对磨削液的影响很小。

2.3 平面磨削楔形区气流场影响因素分析

2.3.1 砂轮旋转速度对磨削区气流场的影响

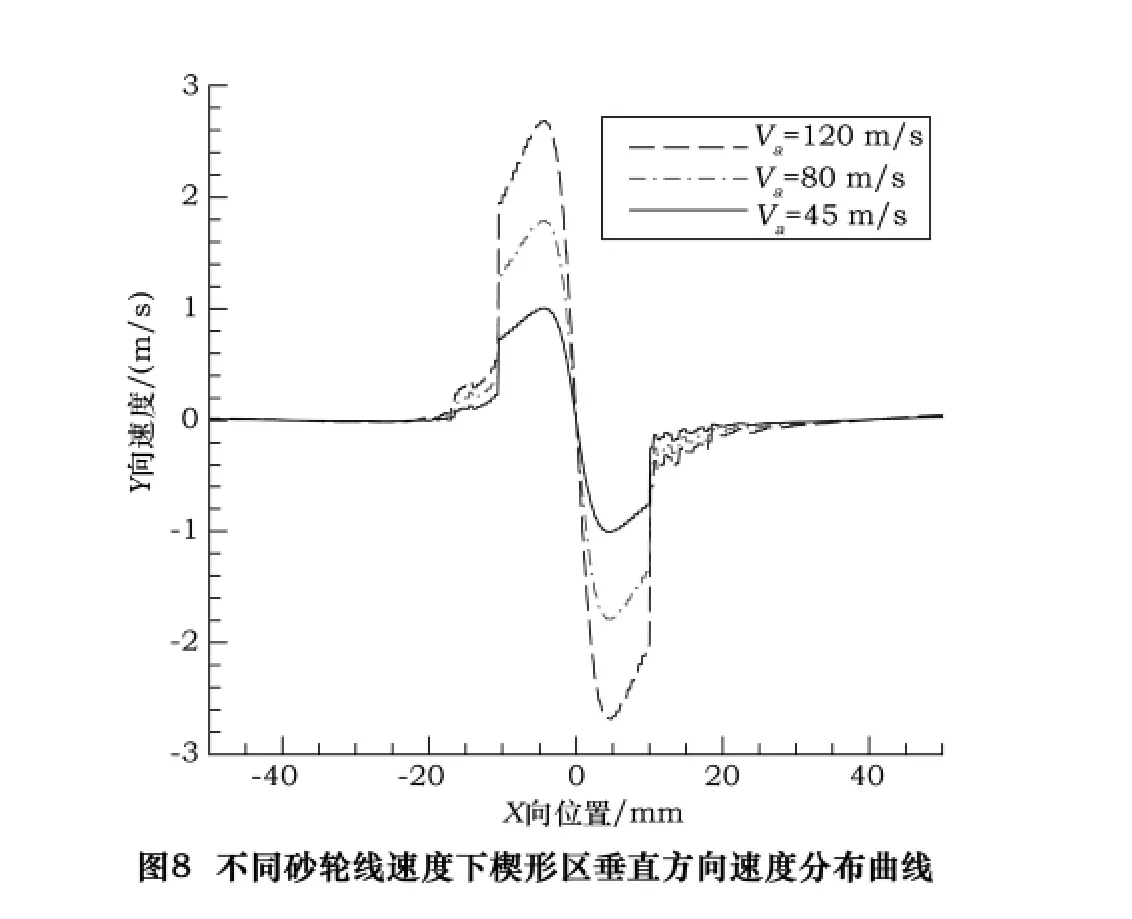
砂轮直径为200 mm，砂轮与工件最小间隙为h0=0.1 mm，在保证上述参数不变的条件下，通过改变砂轮线速度得到磨削区气流场楔形区压力、水平方向速度以及垂直方向速度的变化情况，其中砂轮线速度Va分别取45 m/s，80 m/s以及120 m/s，其变化曲线分别如图6、7和8所示。

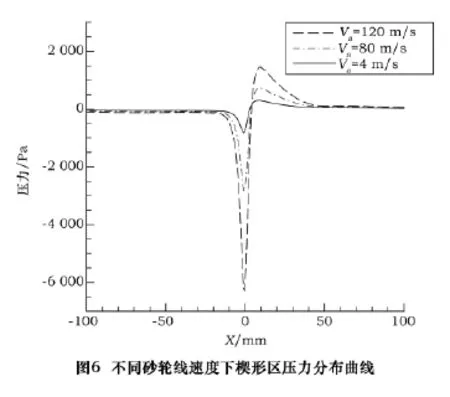
从图6、7以及8可以看出，随着砂轮线速度的增大，楔形区压力、水平方向速度以及垂直方向速度分布规律基本不变，但是峰值均随着砂轮线速度的增大而增大，气流速度也随之增大。而这一切对于冷却液的注入是极其不利的，不能进行充分有效的冷却润滑。当砂轮与工件之间的最小间隙相同时，砂轮线速度对空气水平方向速度的影响很大。砂轮线速度越高，空气水平方向速度曲线的宽度越宽，但对水平方向速度的极值点位置无影响［7］。速度矢量局部放大图如9所示。

分析图9可知，砂轮速度对磨削区气流场气障层及返回流有一定影响，返回流气流速度随着砂轮速度的增大而增大。随着砂轮速度的提高，砂轮周围的气流场速度明显提高，接近砂轮速度的气流层很薄，而且气流层已经裹附砂轮，同时在磨削区内出现了反向气流［8］，特别是在砂轮线速度为120 m/s时，此现象更加突出。

2.3.2 楔形间隙对磨削区气流场的影响

砂轮线速度为45 m/s，砂轮直径为200 mm，在保证上述参数不变的条件下，通过改变砂轮与工件间楔形区最小间隙得到磨削区气流场楔形区压力、水平方向速度以及垂直方向速度的变化情况，其中最小间隙h分别取1 mm，0.5 mm，0.1 mm 以及0.01 mm，其变化曲线分别如图10、11和12所示。

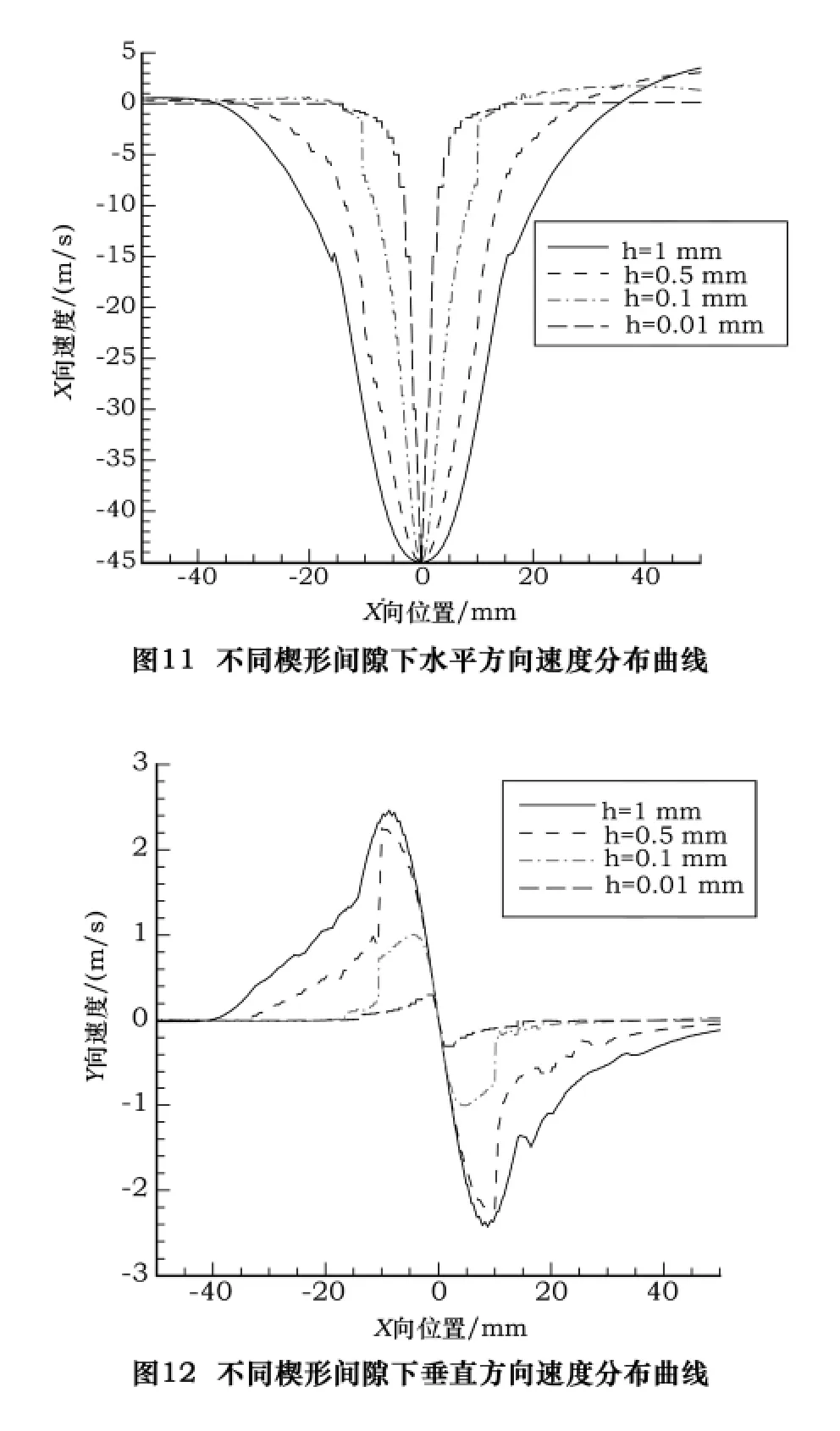
从图10、11以及12可以看出，随着砂轮与工件间最小间隙的减小，楔形区压力、水平方向速度以及垂直方向速度分布规律基本不变，但峰值急剧增大，尤其是最小间隙h0=0.01 mm时，靠近楔形区入口和出口的压力值最大，这对于冷却液的注入有明显的阻碍作用，不能进行充分有效的冷却润滑［9］。砂轮与工件之间的最小间隙越小，空气水平方向速度曲线的宽度越窄，但最小间隙的大小对空气水平方向速度大小的影响程度很小［10］。速度矢量局部放大图如图13所示。

分析图13可知，随着砂轮与工件间隙的变化，砂轮周围的空气气流场也随之发生变化，在砂轮直径以及线速度一定的条件下，最小间隙对磨削区气流场气障层及返回流有一定影响，当最小间隙h0=1 mm时，气障的影响已经很小了，但返回流气流速度随着楔形间隙的减小而增大，这是由于随着楔形间隙的减小，气流越来越难以通过楔形间隙，从而形成更剧烈的返回流。

3 结语

本文根据附面层和流体力学理论，建立了平面磨削气流场理论模型并进行仿真研究，结果表明:

(1)随着砂轮速度的增大，楔形区压力、水平方向速度以及垂直方向速度分布规律基本不变，但是峰值均随着砂轮速度的增大而增大。楔形区入口段返回流气流速度随着砂轮速度的增大而增大。

(2)随着砂轮与工件间最小间隙的减小，楔形区压力、水平方向速度以及垂直方向速度增大，这对于冷却液的注入有明显的阻碍作用。楔形区入口段返回流气流速度随着楔形间隙的减小而增大，这是由于随着楔形间隙的减小，气流越来越难以通过楔形间隙，从而形成更剧烈的返回流。

［1］S.马尔金著.磨削技术理论与应用［M］.沈阳:东北大学出版社，2002.

［2］李长河，原所先，李虎，等.磨削区内气流场速度和压力分布规律的研究进展［J］.金刚石与磨料磨具工程，2004(3):31－34.

［3］巩亚东，王宛山.超高速磨削砂轮气流场基础研究［C］.第三届十省区市机械工程学会科技论坛暨黑龙江省机械工程学会2007年年会论文集，2007，5:23 －35.

［4］Radhakrishnan V.Functional assessment of the grinding wheel surface characteristics by thrbulence amplifier［J］，Journal of Engineering for Industry，1981，103(2):99 －102.

［5］葛培琪，刘镇昌，隋庆华.磨削加工时磨削液的流体动压效应［J］.润滑与密封，2000(1):26 －28.

［6］邓朝晖，荆琦，安磊.纳米结构WC/12Co涂层精密平面磨削表面残余应力有限元模拟与试验［J］.机械工程学报，2008(7):58－62.

［7］李长河，修世超.磨粒、磨具加工技术与应用［M］.北京:化学工业出版社，2012.

［8］Li Changhe，Han Zhenlu，Li Jingyao.Investigation into fluid velocity field of wedge － shaped gap in grinding［J］.Applied Mechanics and Materials，2011，37/38:593 －598.

［9］Sinha，Kuhlman.Investigating the use of stereoscopic particle streak velocimetry for estimating the three － dimensional vorticity field［J］，Exp.Fluids，1992(12):377 －384.

［10］Robinson O，Rockwell D.Construction of three－dimensional images of flow structure via particle tracking techniques［J］，Exp.Fluids，1993(14):257－270.