便携式测量机在曲面件在机测量中的应用
2013-09-27高国防武太文
高国防 武太文 杨 登
(①中国工程物理研究院化工材料研究所,四川绵阳 621900;②63820部队五七五工厂,四川绵阳 621000)
复杂曲面的机械加工误差常以轮廓度表示,在实际曲面测量中,由于产品设计或加工工艺的特殊性等原因,造成曲面测量是无实物基准或基准无法准确定位。在使用三坐标测量机对此类零件检测时,可采用三点找正、模糊匹配等方法[1-2]构建零件坐标系。同时,采用最近邻点迭代匹配算法[3](Iterative Closest Point Algorithm,ICP 算法),两步匹配法[4~9],边界约束BFGS 算法[10](Bound Const Rained BFGS,LBFGS -B)等方法对测量数据与理论模型进行数据匹配,以减小基准定位误差给测量和评定带来的影响。但在使用手动便携式坐标测量机(Portable Coordinate Measuring Machine,PCMM)对复杂曲面零件进行在机检测时,由于无实物基准,采用常用方法建立的工件坐标系误差很大,无法满足要求。针对此问题,本文提出在同一坐标下加工简单结构的基准测量件,结合坐标匹配的方法,较好地解决了该问题。
1 工件检测分析/测量需求
某空气动力学试验用模型件唇部(如图1所示)外形曲面轮廓复杂,根据UG模型编程在加工中心铣削,由于编程方法、刀具补偿、产品本身变形等因素,使得产品加工质量控制难度很大,应尽量避免二次装卡。为控制产品质量,确保产品不报废,需要进行在机检测。本研究中选用的测量设备为Romer-Infinite 2.0 plus便携式测量机,测量范围为1.2 m,示值误差为0.01 mm,测量软件为PC-dmis。
整个模型件表面为曲面,无平面、柱、圆等特征元素。对于此类工件,常用迭代法建立坐标系。需要用所有3组元素(3个用于找平的特征、2个用于旋转的特征和1个用于设置原点的特征)来定义坐标系,且对于特征组中的每个元素,都需要测定值和理论值。PCMM由于是手动测量导致定位精度、重复性差,上述方法不适用。

2 测量方法
2.1 工件坐标系初建
考虑到模型件尺寸不大,加工中心有可用的空间,提出在原加工坐标系(UCS0)下,距离零件尽量远的位置,加工一个结构简单、方便建立坐标系的基准测量件,采用3-2-1法,建立新的坐标系(UCS1)。要求新的工件坐标系与原加工坐标系平行,由于偏移量已知,分别设为Δx、Δy、Δz,则通过以下平移公式可以方便地确定原加工坐标系:
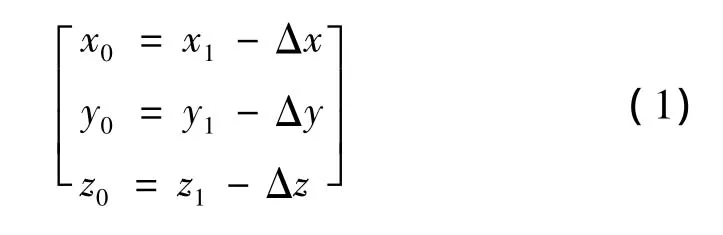
2.2 工件坐标系匹配
由于机床的加工误差会导致基准测量件出现一定的基准定位误差,在UCS1坐标系平移后确定的加工坐标系(UCS0)进行曲面检测时,观察到模型件实测曲面相对于理论曲面有明显的偏移和倾斜,说明建立的坐标系与实际坐标系有偏差,需要通过坐标系的重新匹配来减小或消除。可将测量数据作为一个刚体,相对于曲面的CAD模型,经过坐标变换使得测量数据尽可能地包容曲面CAD模型,并且使测量数据与曲面之间的距离误差最小[10-11]。
假设零件为刚体,这种偏移和倾斜可以归结为刚体平移和旋转,即

其中:Pij=(Xri,Yri,Zri,1),Qij=(Xti,Yti,Zti,1),分别为实测点和理论点坐标的齐次形式,TE为曲面加工综合误差矩阵;TT为4×4变换矩阵,包含了平移和旋转变换。式(2)表明,实测点由理论点经过平移和旋转后得到,正是因此而产生了基准定位误差。由于刚体坐标变换的可逆性,总可以找到矩阵T,使

式(3)表明,实测点经过坐标变换后和理论点重合,消除了基准定位误差。比较式(2)和式(3),T即为TT的逆矩阵,是包含了平移和旋转的坐标变换矩阵,可表示为:

其中:R为旋转因子;P为平移因子;a,b,c为绕X、Y、Z轴旋转角度,rad;tx,ty,tz为X、Y、Z轴上的平移量,mm。
因此,问题转化为求转换矩阵T使得实测曲面(点集P)和理论曲面(点集Q)尽可能重合,重合的过程就是基准定位误差消除的过程。重合后在新坐标系下的测量才能反映真实的轮廓误差,即:

实测曲面和理论曲面的重合问题实际上是实际曲面和理论曲面匹配的问题。由于基准定位误差是在曲面轮廓误差一次测量中产生,这里采用对应特征点构造坐标系匹配法进行实际曲面和理论曲面的匹配。
在实际曲面和理论曲面上分别取3个特征点,记为:Pi,Qi,i=0,1,2,要求三点所围区域覆盖绝大部分曲面。构造以下单位矢量:
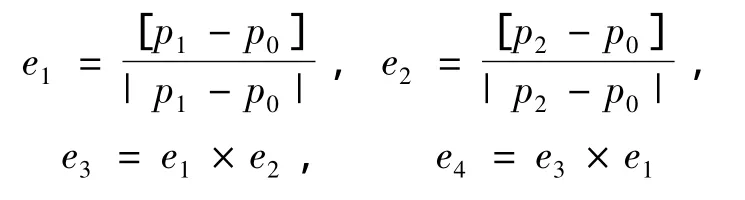

分别以P0为原点和e1、e3、e4为三轴构造坐标系E,Q0为原点和f1、f3、f4为三轴构造坐标系F,假设经过式3变换,坐标系E、F重合,则:
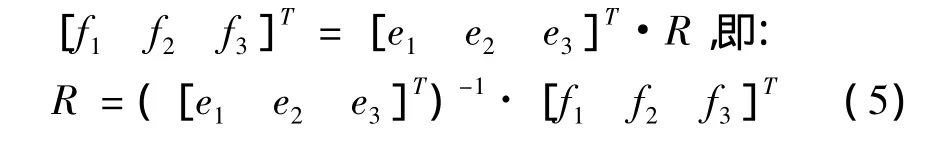
结合式4 和式5 可计算出a,b,c之值,而tx,ty,tz之值可由下式计算得到:

对UCS0坐标系按上述参数进行平移和旋转,即可得到匹配后的坐标系。
2.3 测量与计算
在加工中心上一次加工好模型件(图2)和基准测量件(图3),利用基准测量件上的上平面、圆柱、侧面直线等元素采用3-2-1法建立工件坐标系UCS1,按照公式1平移后得到模型件的加工坐标系UCS0。导入加工用CAD模型,在模型件曲面上均布采点,测量软件根据采点位置在理论模型上查找理论值,评价各点偏差。此时,由于基准定位误差,导致测量结果偏差很大,多数点超差。



将所有测量点构造成特征组,使用特征组最佳拟合坐标系,软件将按照上述方法对坐标系进行最佳匹配,产生新的坐标系,使得测量数据尽可能地包容曲面CAD模型。重新测量曲面,结果表明仅局部超差。根据检测结果对模型件修正,按上述方法检测,结果表明全部满足设计要求。经台式三坐标测量机上检验结果验证,在机检测数据达到控制加工质量的预期目的。
3 结语
由于基准定位误差是曲面轮廓测量误差的主要来源,故可通过对测量数据的匹配计算,对坐标系进行平移和旋转,使得测量数据尽可能地包容曲面CAD模型,也使测量数据与曲面之间的距离误差最小。
在零件坐标系下加工简单结构、便于建立坐标系的基准测量件的方法,在工件相对机床坐标固定的情况下,可以很好地解决复杂曲面在机检测无法定位基准的问题。
[1]王亚平,郑彦龙.三维测量软件系统中坐标系的建立方法[J].工业计量,2004,14(6):27 -30.
[2]黄沛丽.关于三坐标测量机坐标系的建立[J].科技信息,2010(18):112-113.
[3]Besl P J,Mckay N D.A Method fo r Reg istration of 3D Shapes[J].IEEE Transaction on Pattern Analysis and Machine Intellig ence,1992,14(2):239-256.
[4]严思杰,周云飞,彭芳瑜,等.大型复杂曲面零件加工余量均布优化问题研究[J].华中科技大学学报,2002,30(10):35 -37.
[5]严思杰,周云飞,彭芳瑜,等.大型复杂曲面加工工件定位问题研究[J].中国机械工程,2003,14(9):737 -740.
[6]沈兵,帅梅,高君,等.大型复杂曲面类毛坯最佳适配算法的研究[J].西安交通大学学报,1999,33(11):90 -94.
[7]武殿梁,黄海量,丁玉成,等.基于遗传算法和最小二乘法的曲面匹配[J].航空学报,2002,3(3):285 -288.
[8]彭芳瑜,严思杰,周云飞,等.基于能量法的大型叶片毛坯曲面重构[J].机械设计与制造工程,2002,31(4):47 -49.
[9]严庆光,李明哲,李东成.多点成形件检测中三维数据配准方法的研究[J].中国机械工程,2003,14(19):1648 -1651.
[10]刘元朋,刘晶,张力宁,等.复杂曲面测量数据最佳匹配问题研究[J].中国机械工程,2005,16(12):1080 -1082.
