滚动导轨结合部法向动态特性参数的双自由度测试方法*

杨 尧 袁军堂 汪振华 周 乐

(南京理工大学机械工程学院，江苏南京 210094)

滚动导轨作为现代数控机床的重要核心部件，其结合部的动态特性在很大程度上影响着数控机床的刚度、精度以及精度保持性。因此为实现机床结构动态优化设计，提高机床整体性能，对滚动导轨结合部动态特性参数测试方法的研究具有十分重要的意义。

在滚动导轨结合部动态特性参数测试方法上许多学者作了大量的试验研究［1－3］，归纳起来就是采用模态试验的方法识别得到的结构模态参数(主要为模态频率和模态向量)后，再反求动态特性参数(主要为刚度和阻尼)。这其中就存在一个问题，即结构模态参数虽然反映着结构质量和刚度的分布状态，但在选取的某阶显著模态中，模态质量与实际质量间存在误差，因而直接对滚动导轨结合部动态特性参数的准确识别成为一个热点和难点。

在动态特性参数识别上，K.Shye和M.Richardson［4］提出了一个直接由实测频响函数数据计算系统结构的质量、刚度和阻尼阵的方法。M.J.Roemer和D.J.Mook［5］用一种集成算法来识别系统的动态特性参数矩阵。S.Y.Chen［6］等在分离阻尼阵后，对质量和刚度阵进行了估计，提出了一种由实测频响函数估计系统动态特性参数的方法。李杰和陈隽［7］通过对结构动力学矩阵方程的分解，提出了一种在输入信息未知的条件下识别系统动态特性参数的方法。侯军芳等［8］在研究六自由度隔振平台动态特性参数辨识问题时，提出一种基于单点激励法的频响函数分组测试、垂向重心位置迭代辨识和各子系统动态特性参数分别辨识的方法。以上动态特性参数识别法多是应用于建筑学、地震往复试验台反演等问题的研究，而少见对机械结构的动态特性参数辨识。

本文在分析滚动导轨结合部结构以及导轨安装特征基础上，建立直接识别滚动导轨法向动态特性参数的等效双自由度测试模型，并基于测试模型研制滚动导轨法向动态特性参数测量装置，并对GZB45型滚柱导轨进行试验，获得其法向接触动刚度及阻尼数据。

1 滚动导轨结合部动态特性参数测量模型

1.1 滚动导轨结合部特点

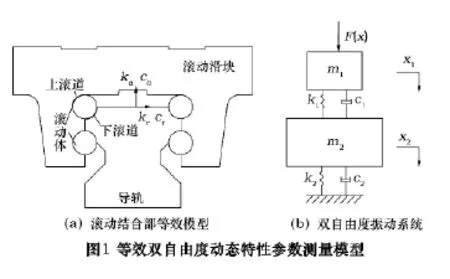
直线滚动导轨结合部主要是由导轨、滚动滑块及滚动体(滚珠、滚柱或滚针)组成，通常采用四列圆弧接触型结构通过上下滚道与滚动体形成滚动结合面，其接触方式为点接触或线接触，结合面处的接触刚度远小于导轨、滑块的结构刚度，因此滚动结合面也是滚动导轨副中的薄弱环节。对滚动导轨结合部动态特性建模实际上就是将滚动结合面处接触动刚度和阻尼等效为法向和切向两个方向上的刚度kα、kr和阻尼cα、cr，如图 1a 所示。

1.2 等效双自由度法向测量模型

数控机床进给系统中，工作台与滚动导轨滑块和导轨与床身间均通过螺栓固连，而滚动导轨结合部中滚动滑块与导轨之间通过滚动体接触连接，因而滚动结合面处的接触刚度也要远小于系统结构刚度，所以可将移动部件和基座看作两个刚性质点m1和m2。滚动导轨结合部与基座和垫铁结合面可视为线性弹簧和粘性阻尼的组合，线性弹簧刚度分别为k1和k2，粘性阻尼为c1和c2。

在正弦力的F(t)作用下建立如图1b所示双自由度振动系统，其运动微分矩阵方程为

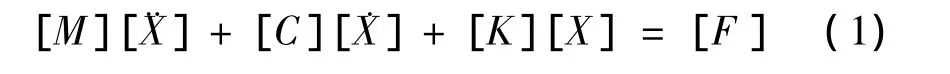
易得其位移频响函数矩阵为:

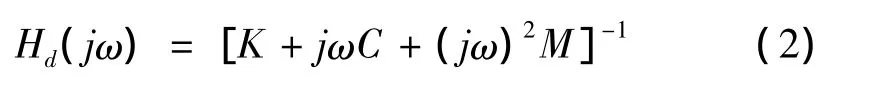
其中，

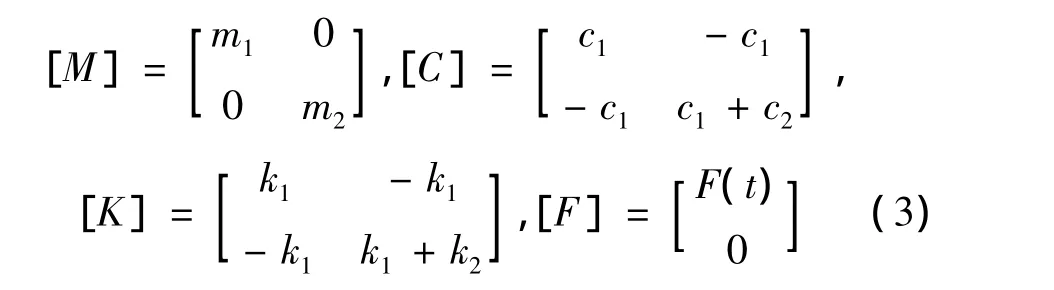
联立式(1)～(3)分别得到移动部件位移频响函数Hd11(jω)和基座位移频响函数Hd12(jω)为

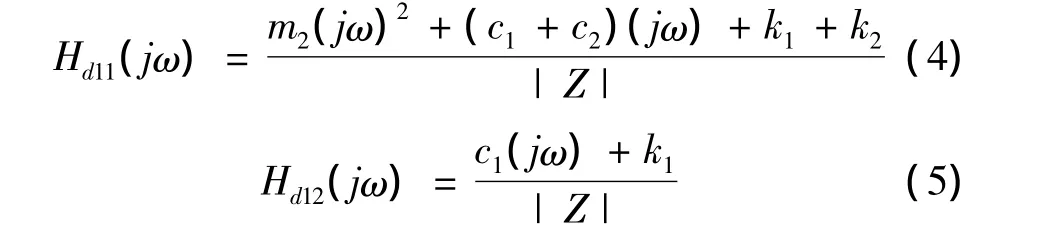
其中特征行列式为:

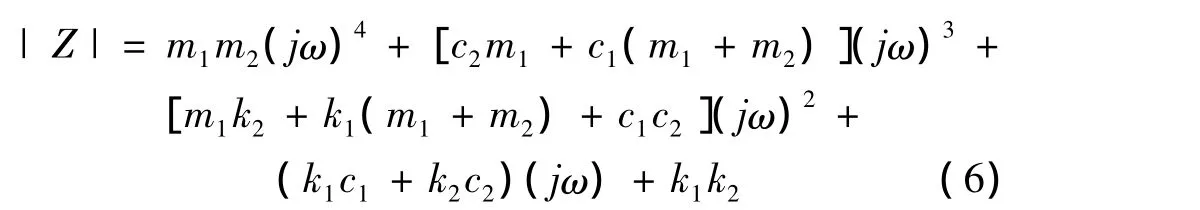
1.3 动态特性参数识别方法

位移频响函数中每个元素都可以写成有理分式的形式，并拥有相同的分母多项式，将位移频响函数的分子分母同除以(m1m2)，并把分子分母多项式按照降幂排列，得到位移频响函数:

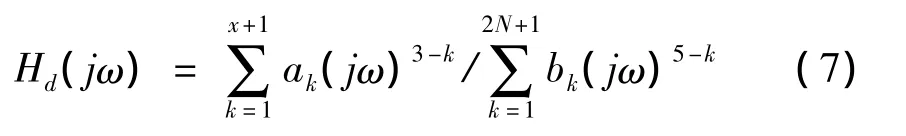
其中，N表示系统自由度数，x=2N－3，b1=1。对于本文N=2。

则可由移动部件和基座频响函数的分子和分母多项式系数推得动态特性参数表达式:

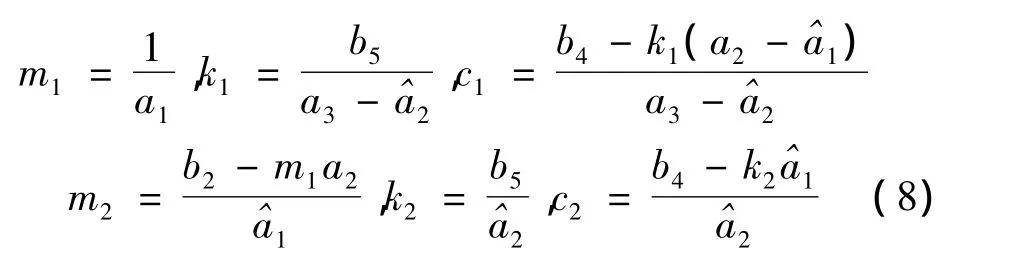
其中，bk(k=1，2，3，4，5)为分母多项式系数，ak(k=1，2，3)为移动部件位移频响函数Hd11(jω)的分子多项式系数，而(k=1，2，3)为基座位移频响函数Hd12(jω)的分子多项式系数。

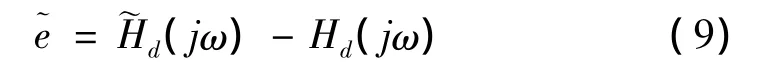
定义目标函数为

采用最小二乘法使得E最小，就可以求解得到式(7)的分子分母系数ak，bk。

根据测得移动部件和基座的位移频响函数，联立式(9)～(11)，并在Matlab中编制了以(jω)为底的幂基多项式拟合程序，分别求出分子与分母多项式系数，就能通过式(8)计算出物理参数。

2 测试装置

结合建立的等效双自由度滚动导轨动态特性参数测试模型，搭建了如图2的测试装置。装置采用双滚动导轨结构，以桥板连接导轨滑块构成移动部件，激振器在桥板上表面中心处激振，导轨与安装板之间用螺栓固连，安装板固定在底座上，底座垂直放置在四块垫铁上，垫铁通过地脚螺栓混凝土结构嵌于地面内。

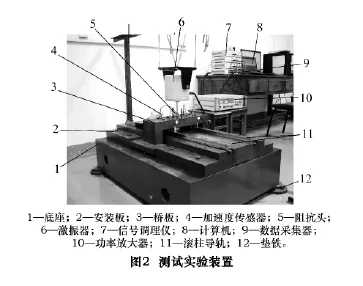
试验时激振器通过刚性细杆连接阻抗头对桥板进行激振，输出的力信号由阻抗头拾取，而桥板及基座的振动加速度信号由加速度传感器测得，力信号和加速度信号进电荷放大器放大后输入到数据采集器中。测试所用的仪器及其主要参数如表1所示。

计算机处理得到的电压信号转化为力和加速值，通过快速傅里叶变换就可以得到各测点的加速度频响函数Hα(jω)，从而易得实测位移频响函数Hd(jω)=Hα(jω)/(jω)2。

表1 实验仪器

3 试验结果与验证

对某装备制造厂生产的GZB45AAMM1P02×1000型滚柱导轨进行了法向物理参数识别。已知移动部件(主要为桥板和滑块)的总质量M1=89 kg。为使得加速度传感器获得很好的精度测量效果并避开刚体模态对试验的影响，取试验的频率采集范围为100～800 Hz，测试试验反复进行多次，任取10次试验，测试计算结果如表2所示。

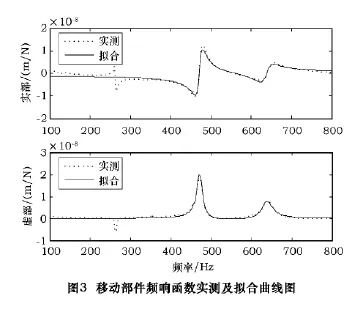
第1组数据的试验得到的移动部件频响函数实测曲线和拟合曲线如图3所示。

采用多次测量取平均值法，计算得到移动部件质量m1=90.69 kg，基座质量m2=2 504.36 kg，k1=1 390.97 MN/m，c1=25 816.4 N·s/m，k2=906.09 MN/m，c2=249 573.5 N·s/m。则单根滚动导轨的法向刚度与阻尼系数为:kα=695.485 MN/m，cα=12 908.2 N·s/m移动部件的实际质量与实测质量的误差仅为1.9%，可见测试结果十分理想。

4 结语

本文对机床进给系统中的关键部件滚动导轨结合部动态特性参数测试进行了研究，得到如下结论:(1)在分析滚动导轨结合部的结构特征基础上，建立了等效的双自由度滚动导轨结合部动态特性参数测试模型，提出动态特性参数识别方法，并根据测试模型研制了测试系统，获得了滚动导轨结合部法向动刚度和阻尼的精确测量方法。(2)以GZB45导轨为研究对象，对其结合部动态特性参数进行了测试，测试结果表明单根滚动导轨的法向刚度与阻尼系数分别为:kα=695.485 MN/m，cα=12 908.2 N·s/m。(3)提出的滚动导轨结合部法向动态特性参数测试方法可以用于识别各种类型的滚动导轨结合部动态特性参数，具有较强的通用性。

表2 测试结果

［1］伍良生，张威，赵宏林，等.数控机床滚动导轨力学性质的实验研究［J］.制造技术与机床，2006(7):26 －28.

［2］李磊，张胜文，于洋，等.滚动导轨结合面参数识别及仿真分析［J］.江苏科技大学学报，2009，23(2):142 －145.

［3］孙伟，汪博，闻邦椿.直线滚动导轨结合部动力学特性测试及参数识别［J］.东北大学学报:自然科学版，2011，32(5):716 －719.

［4］Shye K，Richardson M.Mass stiffness and damping matrix estimates from structural measurements［J］.Proceedings of the 5thInternational Modal Analysis Conference，1987(1):756－761.

［5］Roemer M J，Mook D J.Mass，stiffness and damping matrix identification:an integrated approach［J］.Journal of Vibration and Acoustics，1992，114:358 －363.

［6］Chen S Y，Ju M S，Tsuei Y G.Estimation of mass，stiffness and damping matrices from frequency response function［J］.Journal of Vibration and Acoustics，1996，118:78 －82.

［7］李杰，陈隽.子结构物理参数识别与输入地震动的复合反演研究［J］.振动与冲击，1998，17(1):58 －62.

［8］侯军芳，李荣利，魏火明.六自由度微动隔振平台的物理参数辨识［J］.噪声与振动控制，2011，8(4):73 －76.