三辊斜轧空心减径的辊形设计及实验验证

贾尚武，王召林，刘松，帅全志

(1.中国重型机械研究院股份公司，西安 710000;2.山西王坪煤电有限责任公司，山西 朔州 036000;3.山西省太重煤机煤矿装备成套有限公司，太原 030000)

在生产高精度小直径无缝钢管时，使用冷拔减径工艺的较多。因冷拔工艺在生产过程中容易产生污染，现在被逐步淘汰。在生产小直径无缝钢管的中大型企业中使用定减径工艺的较多，采用空心减径的越来越多。其特点是单机减径量大、工艺灵活、产品调整方便，适于小批量、多规格生产。文中基于小直径无缝钢管斜轧特性和钢管变形的理论基础，对三辊斜轧空心减径过程的工艺原理进行研究，用有限元软件分析辊型在斜轧过程中对钢管变形的影响，并通过工业试验对模拟结果进行验证。

1 辊形设计[1－2]

根据经验公式，轧辊最大直径按式(1)校核:

式中:Dmax为轧辊的最大直径;dmin为轧制后毛管的最小直径;f'为相应两个轧辊间的间隙，f＇=2.5 mm。

轧辊的入口锥角β1的计算如式(2):

式中:β1为轧辊的入口锥角;φ为轧制过程中的辗轧角;β1'为带辗轧角时的入口锥角。

入口锥角β1减小时可以改善咬入条件和轧件内表面质量，但是入口锥角太小，轧件所受到轧辊的压缩次数便会增多，影响成形结果。在实际生产过程中入口锥处可以设置成2个锥角。入口锥角通常取2.5°～4.3°。

三辊空心斜轧时轧辊的入口锥长度计算式为:

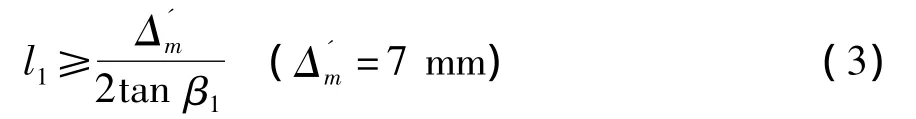
在计算轧辊均整段长度时，为确保轧件的壁厚均匀，轧辊均整段的长度必须使轧件任意截面上金属在均整段上轧制2次以上，所以:

式中:DZ为荒管外径，mm;α为送进角。式中的Zch用最大值代入。

均整段长度的选取由所生产钢管的质量和精度决定。在实际生产过程中，当轧制过程中轧件的内径与外径之比小于0.5时，轧件必须在均整段上经过10次以上的整形才能消除轧件在咬入段及减径段时产生的椭圆度。由于在文中所提到的轧件的内外径之比要大于0.5，所以轧制时轧件在均整段内经历2次以上的整形即可满足要求。当带辗轧角时平整段的辊面角近似于辗轧角φ。

在计算轧辊出口锥角的过程中，轧制厚壁管时，出口锥角β4可选2°～3°，轧制薄壁管时，可选3°～4°。当带辗轧角时，有如下关系:

轧辊出口锥长度的计算如式(7):

对于 DZ/δZ≤12 的毛管，Δ =0.03(dz+ δz)，dz为轧后钢管内径，对于DZ/δZ＞12的管子，Δ取[0.4～0.5]DZ/δZ。

文中实验采用的设备如图1所示，此结构是基于50三辊穿轧机与阿塞尔轧机结构所设计的，最大可轧制坯料为50 mm的管坯。

图1 实验设备Fig.1 Laboratory equipment

由上述公式初步设计的辊型参数见表1。

依据上面的参数，使用三维建模软件ProE建立轧件及轧辊的模型。辊型的二维及三维图如图2所示。

表1 辊型尺寸Table1 The dimensions of roll

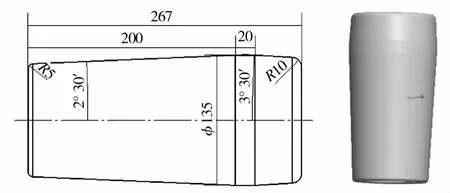
图2 辊型的二维和三维图Fig.2 Roller-type two-dimensional and three-dimensional drawing

2 三辊斜轧过程的有限元仿真模拟

根据以上设计的辊型，应用ANSYS/LS-DYNA大变形弹塑性显示分析动力学模块，进行有限元模拟，分析辊型曲线对成形过程的影响。

2.1 有限元模型建立

在进行模拟时，将外径为 φ42 mm，壁厚为4 mm，长度为150 mm的轧件划分为3600个单元，进行网格划分后的模型如图3所示。

图3 有限元模型Fig.3 Finite element model

模拟时设置的具体参数:轧制温度为1050℃，动摩擦因子为0.25，静摩擦因子为0.35，轧件的初速度为 0.05 m/s。

建立的模拟方案见表2。

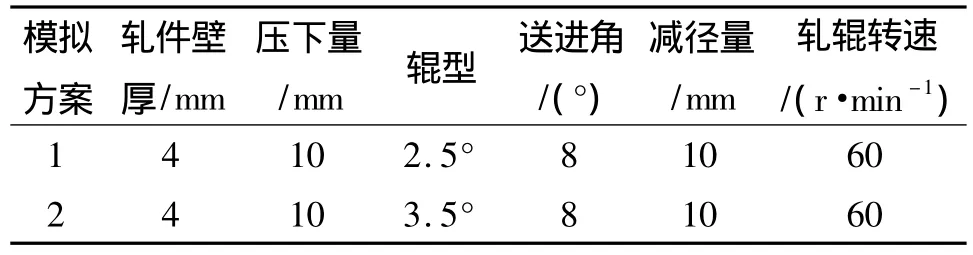
表2 不同的辊型曲线对成形结果的影响Table2 The forming results with the different roll of curves

2.2 模拟结果与分析[3]

按照表2辊型进行模拟，即送进角为8°，壁厚为4 mm，减径量为10 mm时，比较入口锥角为2.5°和3.5°时的轧制力以及应力应变情况。

2.2.1 轧制力分布

轧制力曲线如图4所示。

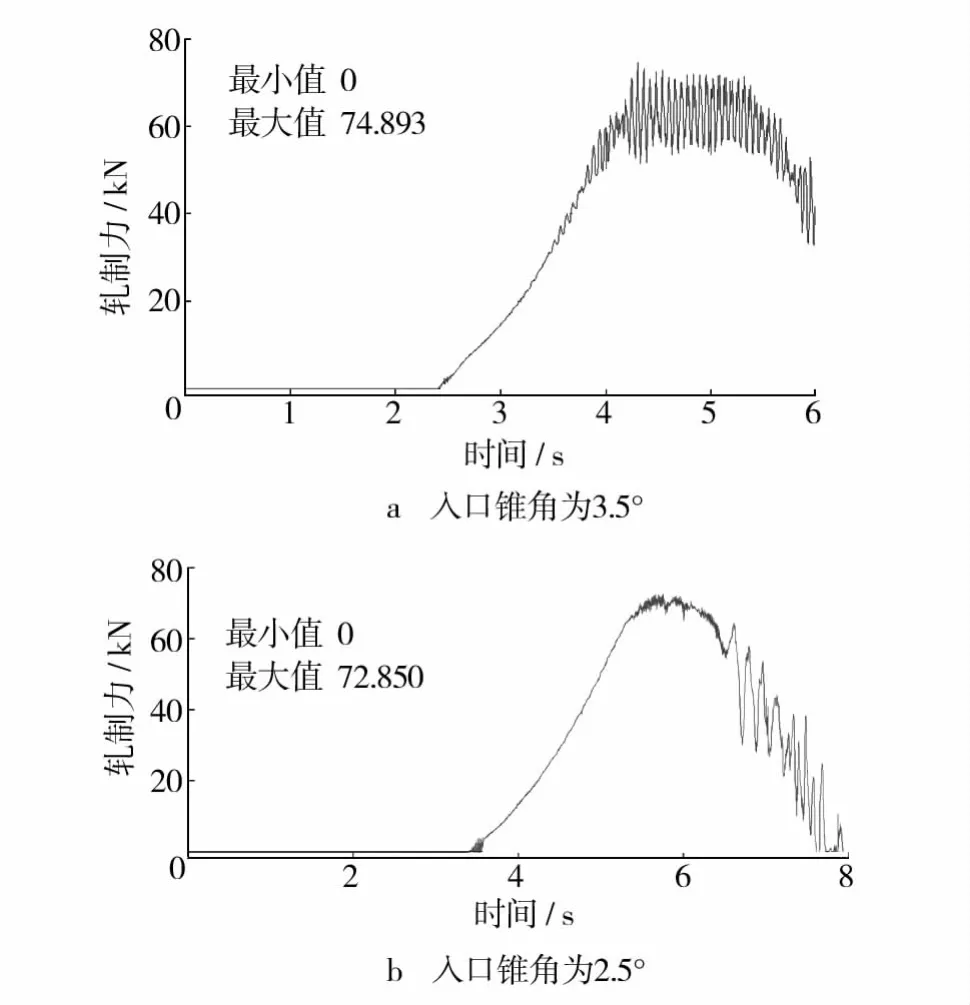
图4 轧制力分布曲线Fig.4 The rolling force distribution curves

由图4可以发现，入口锥角为3.5°时的最大轧制力大于入口锥角为2.5°的最大轧制力，并发现入口锥角为3.5°时的轧制力曲线在最大轧制力附近摆动幅度较大且持续摆动，这说明当入口锥角为3.5°时的三辊斜轧空心过程不稳定。单元沿轧制方向的速度曲线如图5所示，可以发现，入口锥角为2.5°时的轧件单元沿轧制方向的变形速度比较稳定，而入口锥角为3.5°时的轧件单元沿轧制方向的速度波动相对较大。当轧件逐渐咬入时，出现轧制速度突然降低的现象。这是因为刚开始轧件与轧辊接触时有一个咬入的过程，这个时候接触面积非常小，轧辊给轧件的摩擦力很小，但阻力相对较大。

2.2.2 应力与应变分布[4]

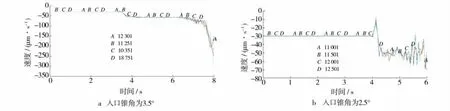
图5 单元沿轧制方向的速度曲线Fig.5 Unit speed curve along the rolling direction

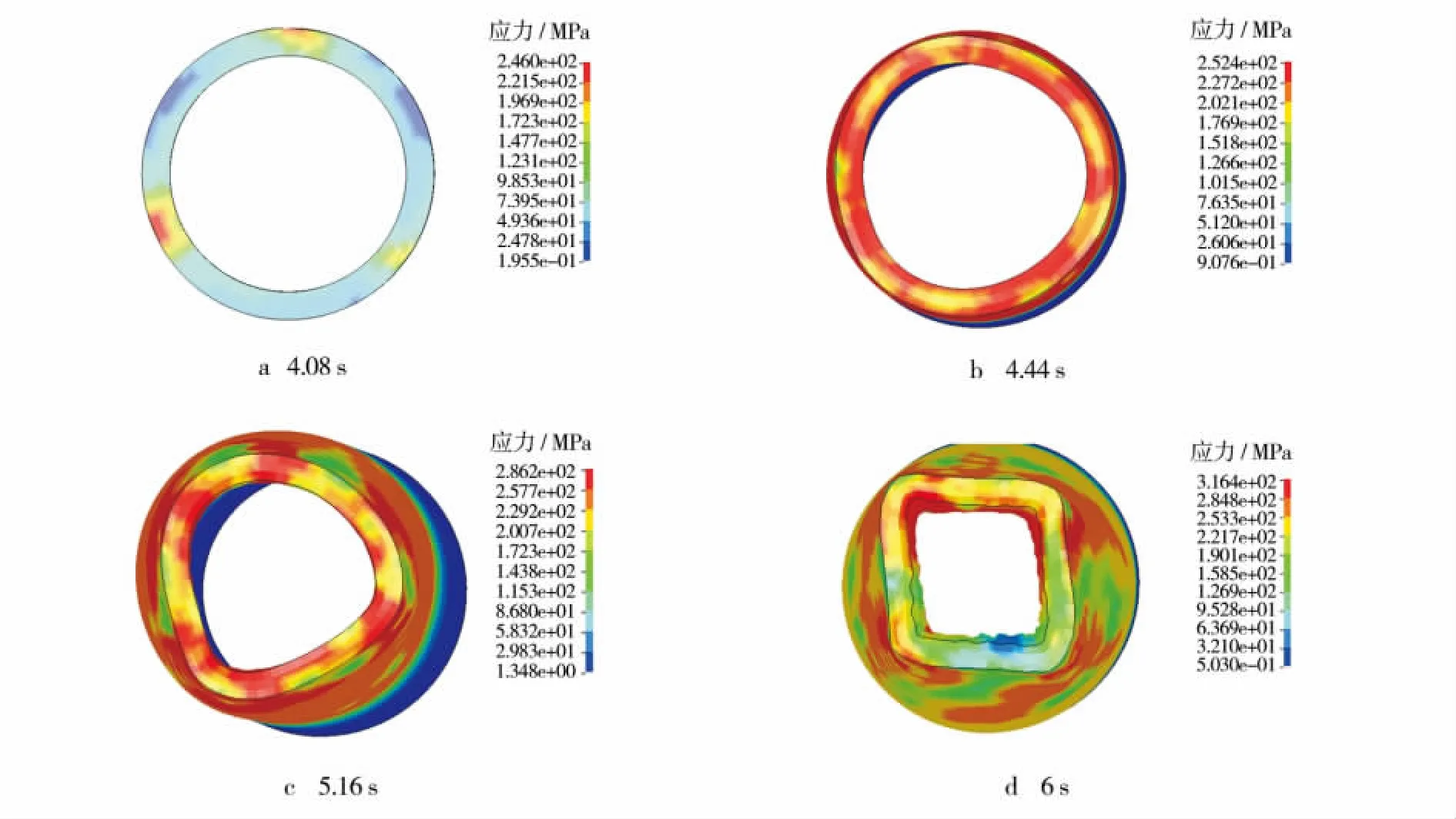
图6 轧制过程中的应力分布Fig.6 Stress distribution of the the rolling process

入口锥角为3.5°时轧件在整个斜轧空心减径过程中代表性时刻的应力分布如图6所示。图6a为刚开始时刻，轧制情况比较正常。从图6b发现，出现了三角形截面，这符合三辊斜轧成形规律，但其中2个顶端已不明显，过渡成圆弧，两边出现了新的顶端，且其中的2组拉压应力均出现在新形成的锥形端部。断面上出现了6个应力集中处，且顶端在一对应力的中间，即拉应力和压应力中间，这也符合三辊成形规律。从图6c发现，轧件端面出现不规则的五边形，也出现了3个拉应力和3个压应力。对比入口锥角为2.5°时产生的这种现象可以解释为:其一，入口锥角变大导致轧件与轧辊的接触面积太小，从模拟结果来看，轧制力比入口锥角为2.5°的大，所以导致轧件受到的单位应力变大，从而引起附加应力增大，使得轧件金属向周向流动加快，从而产生多边形;其二，从轧制力曲线可以看到，轧制过程极不稳定，轧制力不断变化，导致轧件金属在复杂应力作用下形成多边形。

入口锥角为3.5°时轧制过程中各个时刻的应变分布如图7所示，可以发现，入口锥角为3.5°时三辊斜轧空心减径过程中的应变分布随时间的变化由均匀变得不均匀。

从图8可以发现，当轧件斜轧减径后，轧件端面呈正四边形，而且轧件表面产生明显的螺纹状，轧件壁厚极不均匀，内表面质量较差。

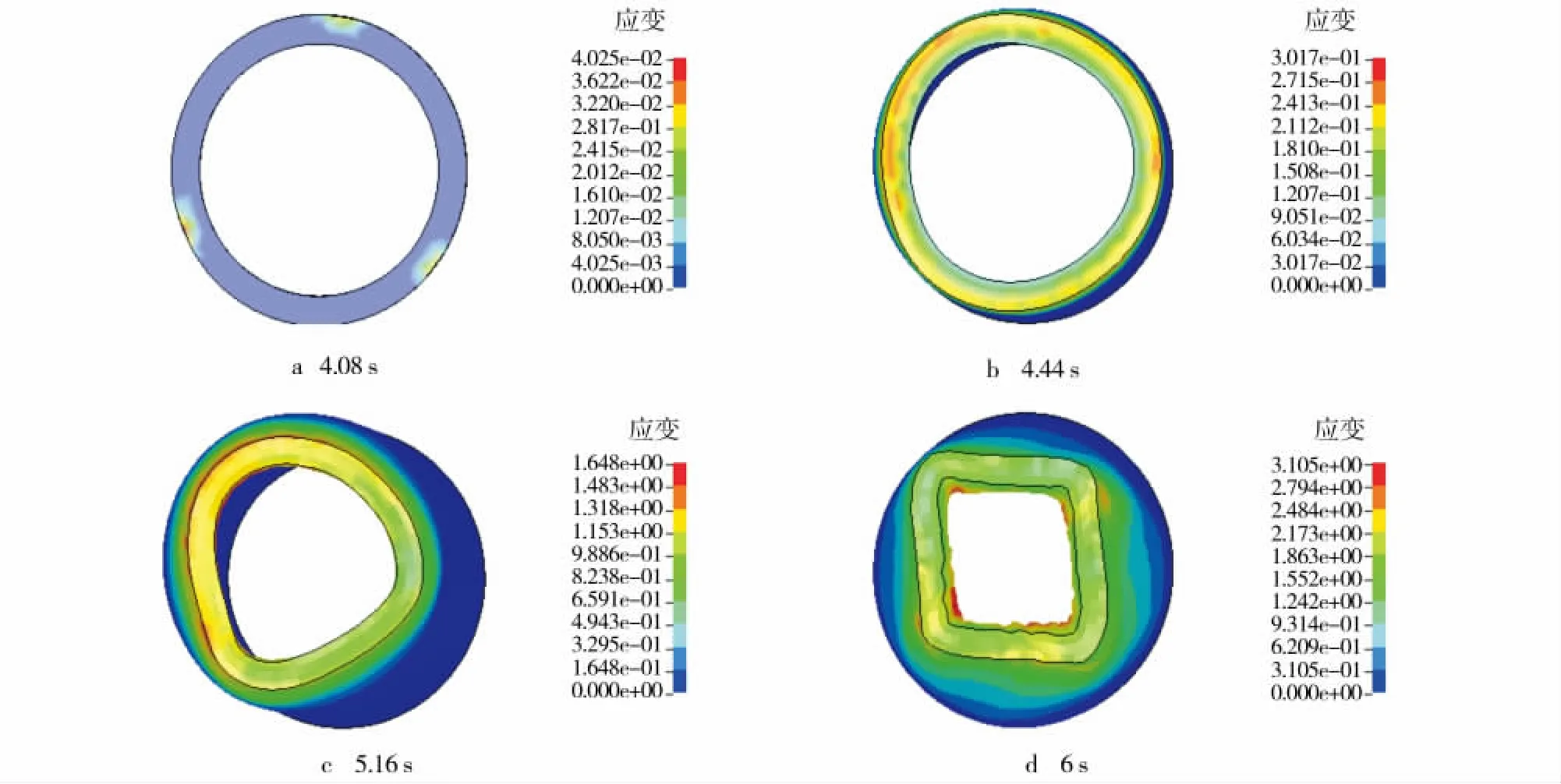
图7 轧制过程中各个时刻的应变分布Fig.7 Strain distribution of the various moments in the rolling process

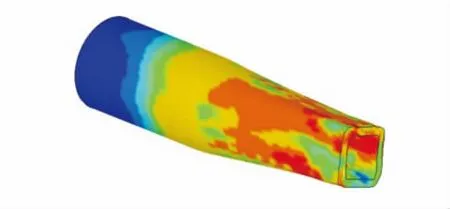
图8 毛管前段成形后的形状Fig.8 Shape of the front part of pipe blank after forming

3 实验过程及结果

为了保证轧制过程的顺利进行以及确保能够正确反映真实的结果，在实验的过程中对同一种方案进行多次测试，最后选择共性的具有代表性的样品进行分析。在实际试验的过程中还将进行一些交叉的数据实验，因此实际实验的方案比模拟的方案多。下面用在给定相关参数进行试验时选出的代表性样品，说明相关参数对成形过程的影响规律。

轧辊在轧制成形过程中起着关键的作用，辊型设计合理是保证工艺成功的关键。由于三辊斜轧空心减径过程中轧辊所受到的应力非常复杂，辊型设计一般不太可能通过纯数学公式计算得到，一般根据现成的理论经验公式计算出初步的辊型，然后使用辊型对轧制成形过程进行有限元模拟，同时通过改变辊型的参数来观察不同辊型参数对轧制结果的影响，最后选择出最合理的辊型。该次的模拟方案选用2组辊型进行试验，最终选择有利于轧制过程成形的辊型[5]。

采用方案1使用2种不同辊型进行轧制时所得到的具有代表性的实验图片如图9所示，图9a，b分别为采用入口锥角为2.5°与入口锥角为3.5°轧制后的结果。从实验结果发现，当采用入口锥角为2.5°的辊型时，能保证轧制出小直径无缝钢管，所以在其他相关工艺参数相同且确定的情况下，与入口锥角为3.5°的辊型相比，从工艺角度来说，当减径量小的情况下采用入口锥角为2.5°更合理。采用入口锥角为3.5°的辊型在轧制过程中会出现轧卡或四边形现象，多次试验结果基本相同。图9c是入口锥角为3.5°的辊型所对应的轧件模拟后的结果，可见，实验结果与模拟结果一致。当对2种不同辊型的方案进行轧制实验时发现，在咬入段，两者的轧制成形相差并不明显，它们的变形都很均匀，轧制过程中，轧件都是经历从圆截面到三角形截面的变形过程。当快接近均整段的时候，入口锥角为3.5°的辊型对应轧件的端面逐渐变成四边形，有时会出现电机保护跳闸的情况。入口锥角为2.5°的辊型对应的轧件在接近均整变形区时金属流动十分平缓和均匀，轧件前端面也从三角形截面逐步变为圆截面。综上所述，最后认定采用入口锥角为2.5°的辊型合理。

图9 辊型对轧制结果影响Fig.9 The rolling results with roll of curves

入口锥角为3.5°的辊型所对应的轧制过程出现四边形现象[6]，其产生的原因很多，包括网格划分不细，轧制条件的设定与真实有差别等。采用入口锥角为2.5°的辊型模拟出的结果较好，是因为轧件在轧制变形的过程中会产生复杂的应力、应变。在沿轧件切向方向上受切向压缩，在轴向方向上受到轴向延伸变形，沿径向方向上所受到的径向压缩是主要的变形，其余2种变形是次要的。由于在轧制过程中金属会向着阻力小的方向流动，所以当轧件在径向方向受到较大的阻力时金属便沿着切向方向进行扩展，这使得轧件的椭圆度增加，最后造成轧卡。

从模拟结果结合实验部分分析可以发现[7]，造成闷车及轧件截面呈四边形的主要变形阶段在减径阶段，主要原因为:斜轧减径过程中轧制带较长时不容易出现截面呈四边形甚至发生闷车现象;当轧件端面上受到的最大等效应力分布比较对称均匀时，轧制出来的毛管效果较好，反之，则易出现多边形截面。通过分析，入口锥角为2.5°时，轧件与轧辊的接触带较长，比入口锥角为3.5°的轧制带长20 mm左右，而且入口锥角为2.5°时轧件端面上的最大等效应力分布也较均匀，而入口锥角为3.5°时轧件端面上受到的最大等效应力分布不均匀，导致四边形截面的产生。

在进行工艺摸索的过程中，发现对于42 mm的棒材，当采用小于10 mm的减径量时，直径方向上壁厚增加约2 mm;当采用小于14 mm的减径量时，直径方向上壁厚增加2.5～3 mm，而长度方向上都有所延伸，呈现出减径量越大，长度方向上延伸越长的规律[8－10]。符合变形规律。

4 结语

通过对三辊斜轧空心减径过程中不同辊型的模拟及实验情况进行对比分析，得到以下结论。

1)当减径量小于10 mm时，最好使用入口锥角为 2.5°的辊型;

2)当减径量在14 mm左右时，应使用入口锥角为 3.5°的辊型。

实验中轧件的变形规律与数值模拟中大致相同。

[1]王海文，李绍山.三辊轧管机的发展及轧辊辊型设计[J].钢管，1992，21(2):16 －19.WANG Hai-wen，LI Shao-shan.Three-roll Rolling Machine Development and Design of Roll-type[J].Pipe，1992，21(2):16 －19.

[2]刘立忠，刘相华，王国栋.轧制过程的显式动力学有限元模拟[J].力学与实践，2001，23(5):34 －36.LIU Li-zhong，LIU Xiang-hua，WANG Guo-dong.Rolling Process Explicit Dynamic Finite Element Simulation[J].Mechanics in Engineering，2001，23(5):34 －36.

[3]沈红伟.中空钢三辊斜轧过程的数值模拟[D].秦皇岛:燕山大学，2009.SHENG Hong-wei.Three Hollow Steel Rolling Process Simulation[D].Qinhuangdao:Yanshan University，2009.

[4]李晓红.我国小直径无缝钢管生产发展与装备选择之探讨[J].钢管，2012，41(1):14 －22.LI Xiao-hong.Development of Small-diameter Seamless Steel Pipe Production Equipment Choice and Explore[J].Pipe，2012，41(1):14 －22.

[5]常建设，庄钢，钟锡弟.我国小直径无缝钢管生产机组的发展[J].钢管，2012，41(5):15 －21 CHANG Jian-she，ZHUANG Gang，Zhong Ti－ Di.China＇s Small Diameter Seamless Steel Pipe Production Unit Development[J].Pipe，2012，41(5):15 －21.

[6]杨志强.三辊轧管的几个工艺问题[J].钢管，1989，19(5):8－10.YANG Zhi-qiang.Three-roll Rolling Process Issues[J].Pipe，1989，19(5):8 －10.

[7]胡友民，杨文华.Transval型三辊轧管机活动机架液压回转机构数学模型推导[J].武汉冶金科技大学学报，1996，19(2):198 －202.HU You-min，YANG Wen-hua.Mathematical Model of Hydraulic Rotating Mechanism for The Transval Type 3-rollTube Mill＇s Moving Housing[J].Journal of Wuhan University of Science and Technology，1996，19(2):198 －202.

[8]MEDINA S F，MANCILLA J E.Static Recrystallization Modelling Of Hot Deformed Steels Containing Several Alloying Elements[J].ISIJ International，1996，36(8):1070－1076.

[9]李云霞.轧制过程的有限元模拟[D].昆明:昆明理工大学，2009.LI Yun-xia.Finite Element Simulation of Rolling Process[D].Kunming:Kunming University of Science，2009.

[10]GULYAYEV YU G，MAMUZIC＇Ilija，SHYFRIN YE I，et al.Perfection of Processes of Seamless Steel Tubes Production[J].Garmashev Metalurgija，2011，50(4):285 －288.