对海上落水人员漂流轨迹的预测研究

刘凯燕

（上海海事大学 信息工程学院，上海 201306）

随着我国海洋经济的发展，海上遇险事故的发生也在所难免的避免。如何在海难事故发生后尽快的找到遇难人员，减少生命损失一直都是研究的重点[1]，也是我国目前海上搜救研究的难点。海上搜救是我国根据《1979年国际海上搜寻救助公约》所承担的一项重要国际义务和一项十分重要的社会职能，也是我国履行国际义务，维护良好声誉的要求。

国内外学者对海上漂浮的漂移特性都进行了许多实验和研究。其中，Allen A和Plourde J.V等人[2]在总结前人研究的基础上对风压作用漂浮物的运动特性进行了比较系统的研究，将海上漂浮物进行详细分类，并通过线性回归的方法建立了风压与海面10 m高处风速之间的线性经验回归方程。Breivik等[3]建立了挪威海和北海的搜救模型，其流场计算采用POM模式，并采用了蒙特卡洛算法确定搜寻区域，计算效果较好。国内于卫红等[4]通过计算海流、风生流、风压差等对搜寻目标的影响，预测搜寻基准，并考虑位置或然误差、可用搜寻力量和覆盖因数等，对搜寻区域确定进行研究，建立搜寻区域确定模型，但模型是基于解析法，整体误差过大。对此本文以落水人员为研究对象，利用粒子仿真法在计算机上模拟目标漂移的概率过程，讨论了对流场数据进行线性插值算法之后，漂移模型的误差变化。

1 海上落水人员漂移数学模型

一般而言落水人员在海面上可以看做是无动力漂移目标，在不考虑垂向运动的情况下，受风、浪、流三类力的共同影响在海面上水平漂移[5]。当目标长度（一般小于50米，包括船舶碎片、落水人员、救生筏等）相对于海浪波长较小时，忽略波浪的影响 ，即对于海上落水人员而言，漂移速度主要受到了两方面的影响，即暴露于海面上的身体部分所受到的风致漂移和身体在海水中的部分所受到的流速漂移，则目标的漂移速度为：

式中，VL为目标的风致漂移速度，VC为表层海流的流速（文中采用海面下0.5 m处的流速），根据目标的受力分析可知目标的漂移运动方程[8]为：

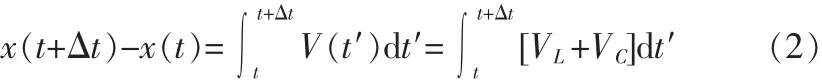
2 风致漂移和流场数据线性插值

2.1 风压分解

风致漂移是由于漂浮物暴露于空气中的部分受到风压作用引起的。将风压分解为顺风分量（DWL）和侧风分量（CWL）[6]，如图1所示。风压角存在一定的不确定性，即风压角可能是在风速顺时针偏右方向，也可能是在相反方向，定义在风速方向偏右的侧风分量为正，偏左为侧风负分量。因此，漂浮物也可能向左右漂移，在初始条件下，目标向两个方向漂移的概率是均等的，但在确定目标在某一方向漂移后，它的漂移方向将不会改变。

图1 风压分解图Fig.1 Wind pressure exploded

由于目标的形状、大小以及位于水上和水下的部分面积之比都对风致漂移产生了很大影响，则不同的海上漂移物体拥有不同的漂移特性，所以一定的风速对其的影响也不尽相同，国内外的学者都对不同的漂流目标进行了不同的实验研究。1999年美国海岸警卫队Allen Plourde等[7]人对不同类型搜救目标的风压试验数据进行了总结，并确定了不同类型的漂浮目标的风致漂移速度与海面上空10 m高处的风速之间的关系。

2.2 无约束风压模型（风压Y-模型）

风压O-模型是在现有的经验数据上增加约束条件统计回归得到的，顺风方向风压矢量、侧风方向风压矢量与海面10 m高出风速之间的线性回归方程为:

通过查2005年Allen建立的Leeway Formula Table风压系数表可知，aDWL=0.017 1，aCWL-=0.013 6。为了弥补风压试验中数据采集中所存在的误差，将风压系数进行小幅的扰动，扰动公式为：

对上述模型进行1 000次扰动以后，顺风分量的风压经验估计值与海面10 m高处风速之间的关系图2所示，虽然风压O-模型在速为0时，顺风分量也为0，但在风速较小时也可能产生较大的误差。

2.3 流场数据的线性插值算法

流场数据的精确度越大，我们对目标漂移的预测误差就越小。为了更贴近的表示海上流场数值的变化，在流场计算过程中一般是使用插值函数来描述内部各个点的值。插值的目的就是数值逼近的一种手段，而数值逼近，为的是得到一个数学问题的精确解或足够精确的解。内插法是已经长期使用的传统方法，其主要缺点是计算具有很大的盲目性和随意性，但由于该方法简单易于计算，还能长期存在下去。

图2 O-模型顺风分量风压经验值与海上10 m高处风速关系图Fig.2 Relationship diagram of the wind speed at 10 m and the tailwind component of the O-wind pressure model

线性插值是数学、计算机图形学等领域广泛使用的一种简单插值算法。 假设我们已知坐标（X0，Y0）和（X1，Y1），要得到这两点之间的某一点的坐标，根据图3所示，我们得到（YT0）（X1-X0）=（Y1-Y0）（X-X0）。假设方程两边的值为 a，那么这个值就是插值系数从X0到X的距离与X0到X1距离的比值。由于X值已知，所以可以从公式得到a的值。这样就可以求得两点之间的任何一点，这种方法就叫作线性外插，如图3所示。

图3 线性插值示意图Fig.3 Schematic diagram of linear interpolation

在流场插值计算过程中，为了贴近实际流场变化，我们将时间分割。将采样间隔的这段时间内分割为更小的时间段，采用插值算法获得未知数据，满足空间数据建模的需要。通过对流速的扰动来模拟实际海上流速的变化，减小误差。本文所采用的流场采样数据一般是间隔10分钟的采样值，在之前的研究中我们都认为在这10分钟内流场值是保持不变的，即使扰动也是小幅的随机扰动，并在10分钟之后的一段时间内流场值直接采用另一采样值。那么，其实在这10分钟内的流场值肯定不是保持不变的。因此，本文考虑采用流场插值来模拟实际流速的变化，流场插值的间隔文中采用1分钟。在采集数据的时间段内，认为流速在更小的时间段内是保持不变的，即如图4所示。

3 实验和实例分析

3.1 实验方法

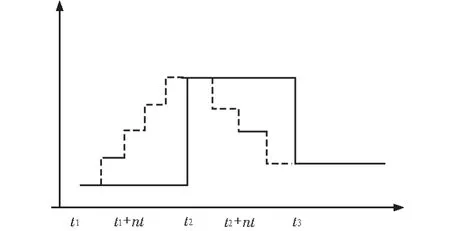
图4 对流场数据进行线性插值算法后的示意图Fig.4 A schematic diagram of calculating the flow field data by linear interpolation algorithm

利用蒙特卡罗法将搜寻目标抽象成粒子，对每个粒子都赋予目标的一切属性并受外部海洋环境的作用而产生漂移，并大量复制这些粒子，最终通过确定粒子群中心点的漂移轨迹来作为目标的预测漂流轨迹。 蒙特卡洛 （Monte Carlo）模拟[8]又称随机模拟（Random simulation）方法，有时也称为随机抽样（Random Sampling）技术或统计试验方法，是20世纪40年代美国科学家Velleman和Von Neumann首先应用于原子弹的研制并以摩纳哥世界闻名的赌城Monte Carlo命名的一种数值计算方法。它是一种通过设定随机过程，反复生成时间序列，计算参数的估计量和统计量，进而研究其分布特征的方法。一般将被抽象为粒子的目标在海面上漂流的过程描述为马尔科夫过程，该过程被称为零阶马尔科夫模型或随机游走模型[12]，即粒子在漂浮过程中t+1时刻所处的位置仅仅与t时刻所处的位置相关。在此，假设每个粒子相互独立，则为了表征每个粒子自己的特性，将风速和流速的大小进行微小的扰动。

3.2 实例分析

文中采用的是美国佛罗里达州大西洋大学所进行的穿救生衣落水人员漂流实验数据[9]，并在Matlab中进行了仿真[10]。为了讨论流场数据的精确度对落水人员的漂流预测轨迹的影响，假设初始位置误差为0，即以事发的初始位置为中心，以100 m为半径，在此圆中释放10 000个成正态分布的粒子。在这里将实验数据的初始时间设置为0，观察随着时间的增长，粒子群中心点的漂流轨迹，并与目标的实际漂流曲线相比较。文中以粒子群中心点位置到目标实际位置的空间距离作为误差，部分实验结果如下图所示。

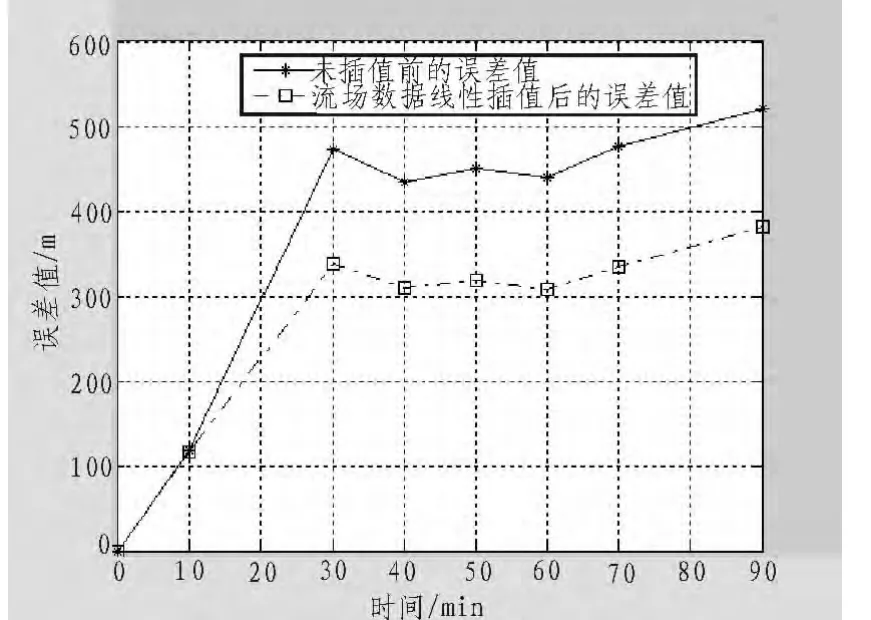
图5 A3-B组数据的仿真图Fig.5 Group of A3-B data simulation

图6 A6-O组数据的仿真图Fig.6 The group of A6-O data simulation

图7 A8-O组数据的仿真图Fig.7 The group of A8-O data simulation

通过实验证明随机粒子仿真法较能够准确地预测目标的漂移轨迹，当风速和流速比较稳定的时候，利用实验数据比较能够准确的拟合漂流曲线，但当风速或流速出现较大地突变时会使得漂流预测轨迹出现大的偏移。 由于对于海上落水人员而言，流速的变化对其的漂移影响比较大，所以流场数据的精确度对模型的实验误差有着至关重要的作用。为此，利用线性插值算法对流场数据进行处理，增大其在时间上的精确度。实验结果也表明了对流场数据进行线性插值后的误差均有所减小。

4 结束语

近年来我国的海上救助活动已引起了广大的社会关注度，而海上救助成功率也是衡量一个国家的发达水平。对海上漂浮物的漂移特性进行研究能够为海上搜救行动提供方向和位置支持，缩短搜救时间，具有很大社会意义。文章通过分析影响海上落水人员漂移的因素，采用蒙特卡罗法对其在相同的实验条件下，流场数据插值前后的误差进行了比较，试验表明将流场数据进行线性插值后的模型具有较好的效果。但文中只对流场数据的线性插值算法进行了探讨，缺乏对其他插值算法研究和比较，以及对如何进一步结合现有的流场预测模拟算法，减小预测误差，将是下一步研究的关键问题。

[1]王焕.我国海上搜救情况浅析[J].天津航海，2010（3）:59-61.

WANG Huan.Analysis of the situation of China’s maritime search and rescue[J].Tianjin Navigation，2010（3）:59-61.

[2]Allen A.Leeway divergence[R].USA：US Coast Guard Research and Development Center，2005.

[3]姜华林.海上搜救中搜寻区域的确定模型研究 [D].大连:大连理工大学，2011.

[4]于卫红，贾传荧.海上搜救中搜寻区域确定方法研究[J].中国航海，2006（2）:34-37.YU Wei-hong，JIA Chuan-ying.Maritime search and rescue search area method for determining[J].Navigation of China，2006（2）:34-37.

[5]刘海峥，赵怀慈，赵春阳.基于Monte Carlo方法的搜救区域预测算法[J].船海工程，2010，39（2）:132-135.

LIU Hai-zheng，ZHAO Huai-ci，ZHAO Chun-yang.Search and rescue region prediction algorithm based on the Monte Carlo method[J].Ship and ocean engineering，2010，39（2）:132-135.

[6]肖方兵.海上搜救决策支持系统关键技术的研究 [D].大连:大连海事大学，2011.

[7]Allen A A，Plourde JV.Review ofLeeway:Field Experiments and Implementation，No.GGD-08-99[R].U.S.Coast Guard Research and Development Center Report，1999.

[8]刘儒勋，王志峰.数值模拟方法和运动界面追踪[M].北京:中国科技大学出版社，2001.

[9]娄安刚，王学昌，于宜法，等.蒙特卡罗方法在海洋溢油扩展预测中的应用研究[J].海洋科学，2000，24（5）:7-10.

LOU An-gang，WANG Xue-chang，YU Yi-fa，et al.Monte carlo method in marine oil spill extended forecast[J].Marine Science，2000，24（05）:7-10.

[10]韩利竹，千华.MATLAB电子仿真与应用[M].北京：国防工业出版社，2003.