基于预测型灰色控制的列车自动运行速度控制器建模与仿真
2013-09-25陆小红王长林
陆小红 王长林
(西南交通大学信息科学与技术学院,610031,成都∥第一作者,硕士研究生)
对于城市轨道交通系统高效率高密度的要求来说,列车自动运行(ATO)系统是轨道交通列车自动控制(ATC)系统的重要组成部分,也是必须解决的关键理论和技术问题之一。在对其进行国产化过程中,ATO控制算法的设计是最重要的内容。
20世纪60年代开始,将经典控制理论PID(比例积分微分)控制运用到ATO当中,利用PID控制的稳态误差实现ATO速度的准确调整。但是,PID控制存在着响应速度慢和控制速度时操作档位切换次数过多的缺点。20世纪80年代,随着智能控制算法的兴起,开始利用模糊控制、专家系统控制以及神经网络控制等智能控制算法来控制ATO系统[1]。模糊控制主要是根据经验定控制规则,专家系统控制主要模拟人类专家解决领域问题;这两种控制方法均存在对人类经验依赖性太强的问题,神经网络控制的自学能力强,但不能解释自己的推理过程[2-4]。由于上述智能控制方法存在一定的缺点,需要寻求新的控制理论应用于ATO系统。
1982年,邓聚龙教授提出的灰色系统理论[5],主要应用于信息不完全性和非唯一性的系统,体现决策多目标、方法多途径,定性与定量相结合以确定一个或几个满意的解。它与ATO系统具有较好的贴合性,可应用于ATO控制。又由于灰色理论分析的系统是少数据不确定系统,故需要结合预测算法来预测形成更多的数据和信息,在线滚动优化和反馈校正,以便更好地应对环境的变化和干扰的存在。
1 系统分析与控制算法提出
ATO速度控制器为达到舒适、节能、准时的运行并精确停车的控制目标,根据对已知的授权和列车当前速度、位移,以及之前的速度、位移、档位等已知信息的分析,参考运行模式曲线,决策下一周期应采用的档位,传送到车辆接口进行速度控制。分析可知,与“大样本不确定性”系统用模糊理论相比,ATO速度控制器的“少样本不确定”性,更符合灰色系统部分信息已知、部分信息未知,主要通过对“部分”已知信息的生成、开发,提取有价值的信息,实现对系统运行行为、演化规律的正确描述和有效监控的特征,故本文采用灰色理论来构建列车自动运行控制的数学模型。其中:运行模式曲线的速度、位移、档位、时间形成了参考序列,即速度控制器的理想方案;计算采用不同档位作用下的各方案与理想方案间的灰色关联度(关联度越大,则方案与理想方案越接近,也就越优)。即采用灰色关联分析对其进行方案决策。
由于跟随性、舒适性、准时性、节能性和停车精度等性能指标对ATO速度控制器计算操纵变量(牵引、制动、惰行、巡航档位)的影响不一致,故需根据各性能指标的影响度分配权重,从而使各方案与理想方案之间的灰色关联度更能体现各决策目标的影响。
对于ATO速度控制器这个非线性、大滞后、多目标、多变量的复杂系统,模型预测控制技术能显示出良好的控制性能。相对于经典的PID控制,它是根据过程当前的和过去的输出测量值和设定值的偏差来确定当前的控制输入,预测控制以根据对象的历史信息和未来输入预测其未来输出的预测模型为基础,采用在线滚动优化指标和反馈校正策略,既具有优化功能又利用了实时反馈信息,结合了最优控制与反馈控制的特点,力求有效地克服被控对象的不确定性、迟滞和时变等因素的影响,并使系统具有良好的鲁棒性。因此,将预测控制思想与灰色控制策略相结合是解决具有不确定性、非线性、迟滞和时变的速度控制器系统控制问题的重要手段。基于预测型灰色系统理论的ATO速度控制器流程如图1。
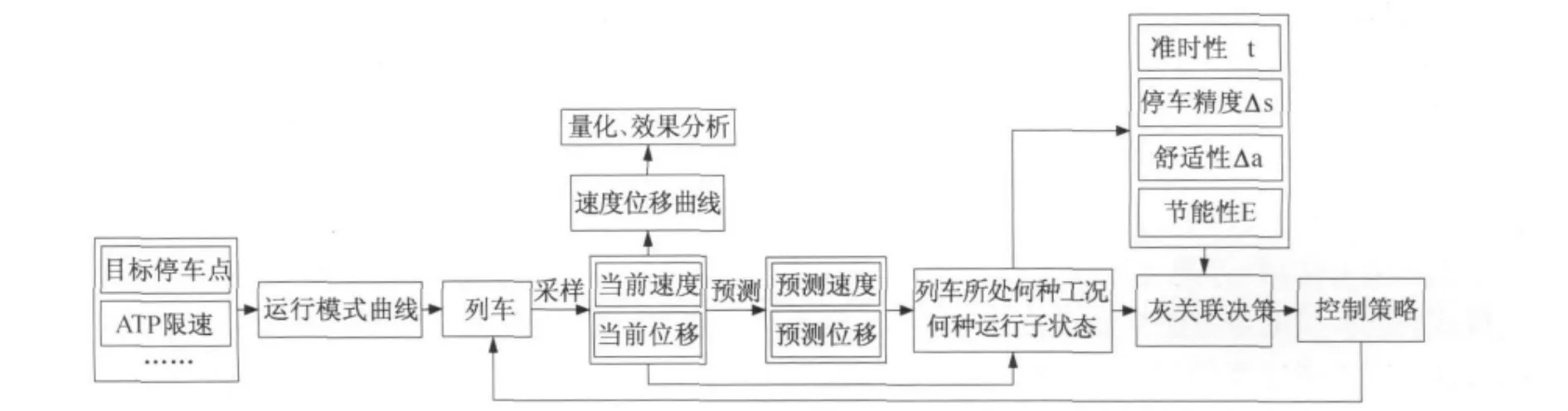
图1 基于预测型灰色系统理论的ATO速度控制器
2 基于预测型灰色控制的速度控制器建模
本文的ATO控制目标是速度控制器满足舒适性、节能性、准时性、高效性、停车精度等性能指标。其具体表征方法如下。
舒适性指标:用加速度变化率Δa来表征舒适性。

式中:
at——本周期列车加速度,m/s2;
a0——上周期列车加速度,m/s2;
Δt——时间步长,s。
Δa越小即舒适性越好。
节能性指标:列车牵引制动力所作的功E来表示能耗。E越小即节能性越好。
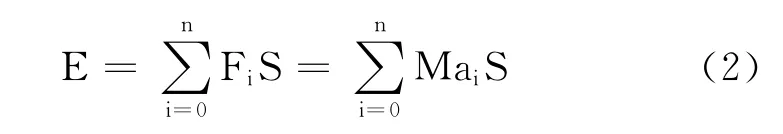
式中:
M——列车载重,kg;
ai——列车加速度,m/s2;
S——列车运行距离,m;
n——加速度变化次数,次。
准时性指标为列车实际运行时间与计划运行时间的差Δt。
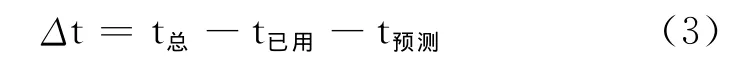
式中:
t总——列车规定运行总时间,s;
t已用——列车已运行时间,s;
t预测——预测列车距停车还需使用时间,s。
Δt越小准时性越好。
停车精度指标为列车实际停车点与目标点的距离Δs。

式中:
s目标——目标停车点,m;
s实际——列车实际停车位置,m。
Δs越小即停车精度越高。
为使速度控制器平稳地控车,需要对系统进行误差分析处理。ATO速度控制器根据列车速度位移计算操纵档位时,由于测速误差、定位误差、传输时延、系统计算精度,操作时延及模型误差的存在,导致车辆模型传输给ATO的列车速度位移存在一定的误差,故在档位调整时需考虑误差范围,在误差可接受范围内不进行档位调整。该策略可以在一定程度上保证舒适度和节能性。另经测试,本仿真平台的车辆模型最大定位误差为±4m,最大测速误差±0.8km/h,故在运行过程中,为增加预测的准确性,减少列车定位误差的影响,预测控制均以信标为分割点进行控制。
具体控车过程分为起动、惰行、停车制动三个阶段。
2.1 起动阶段
当列车准备就绪,ATO系统收到列车数据、地面数据及移动授权后,速度控制器参考运行模式曲线;同时为防止因瞬时施加牵引力过大而产生空转打滑,采用逐渐加大牵引力的策略加速起动。当达到最大牵引力作用后,速度控制器每一周期均与运行模式曲线提供的参考速度位移进行比较。当列车当前速度在参考速度的误差范围内,不进行档位的调整,否则根据预测算法计算下一信标处的速度。若预测速度在参考速度误差范围内,则采用预测档位,调整速度。
2.2 惰行阶段
列车在惰行阶段测速较稳定,若此时列车速度与参考速度有误差,由于换挡操作反应时间和定位误差的存在,档位调整后误差增大的可能性极高,故基本采用参考档位的策略。但若速度过大,通过预测控制,在临制动阶段采用制动4档提前制动。
2.3 停车制动阶段
停车制动阶段分成起始制动、减速制动和停车三部分进行分析和决策。
1)列车定位误差的存在,致使列车决策存在更大的困难,故在运行模式曲线进入制动阶段时,速度控制器亦进入制动阶段。
2)其后列车操纵档位的决策采用灰色关联决策在信标定位校正处进行决策。
① 确定事件集A={跟随运行模式曲线,即保证列车速度位移在误差范围内};
确定对策集B={制动4档、制动3档、制动2档、制动1档};
构造局势集S={s11=(跟随运行模式曲线,制动4档),s12=(跟随运行模式曲线,制动3档),s13=(跟随运行模式曲线,制动2档),s14=(跟随运行模式曲线,制动1档)}。
② 确定决策目标:跟随性k1=Δv=v预测-v参考;舒适性k2=Δa=a预测-a当前;准时性k3=Δt=t总-t已用-t预测;节能性k4=ΔE=M·a·s预测。
③ 不同局势下sij在k目标下的效果值:

④k目标下局势效果序列u(k)的均像值仍记为u(k):

考虑决策目标分配权重wk=(w1,w2,w3,w4)
由于运行模式曲线生成时已考虑了准时性、舒适性、节能性和停车精度等性能指标,列车跟随运行模式曲线运行将是较优化的运行策略,故跟随性这一决策目标的权重为0.4,而舒适性、准时性和节能性权重均为0.2,这也是经多次不同权重分配方案实验,具有最优控制效果的权重分配方案。

⑤ 由④结果写出局势sij的效果向量

⑥ 求理想最优效果向量
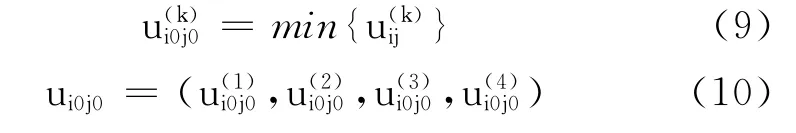
⑦ 计算uij与ui0j0的灰色绝对关联度
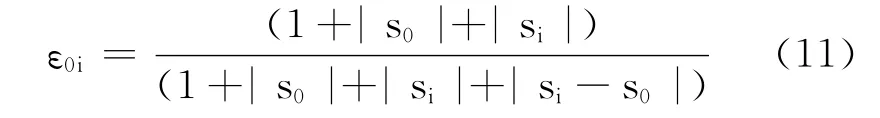
其中,

将根据灰色关联决策定的操纵档位传输给车辆接口,得到次优的控制效果。
3)列车进入站内停车程序后,列车所受制动率由大逐渐变小。当列车速度小于一定速度后,采用恒定制动率将列车停稳。
3 系统仿真与结果分析
3.1 仿真平台
本文的ATO数学模型在ATC仿真平台上进行了仿真。仿真技术平台包括:基于二乘二取二硬件平台的车载ATP,双机热备的车载ATO,ATS(列车自动监控),DSU(轨旁数据单元),ZC(轨旁区域控制单元)与车辆模型(见图2)。其中:车辆模型的主要功能是模拟列车运行,计算列车速度,并将速度值转化为雷达速度传感器和轮轴速度传感器的信号传送给车载ATO设备;同时,车辆模型还根据列车速度计算列车位移,并与地面信标数据库进行核对,向车载ATO发送定位信息。

图2 ATO仿真平台
3.2 仿真过程与分析
列车在模拟线路上运行,预测型灰色控制下列车实际速度距离曲线与参考运行模式曲线贴合度较好。
3.2.1 起动阶段
参考运行模式曲线逐渐增大牵引力,直至列车在最大牵引力下加速运行,如图3所示。

图3 列车起动阶段
3.2.2 停车制动阶段
操纵档位切换点在信标处,故存在图4所示列车速度出现负误差时,减小制动档位,到下一信标处列车超调,根据预测型灰色控制,再调节操纵档位,使列车在目标停车点范围内停车。
3.2.3 列车停车精度分析
参照相关标准定义,停车范围为距目标停车点±0.25m。经千次试验,停车准确度为98.89%,停车误差均值为E(x)==0.13m,标准差为σ(x)==0.743,体现了良好的停车精度和停车误差稳定性。
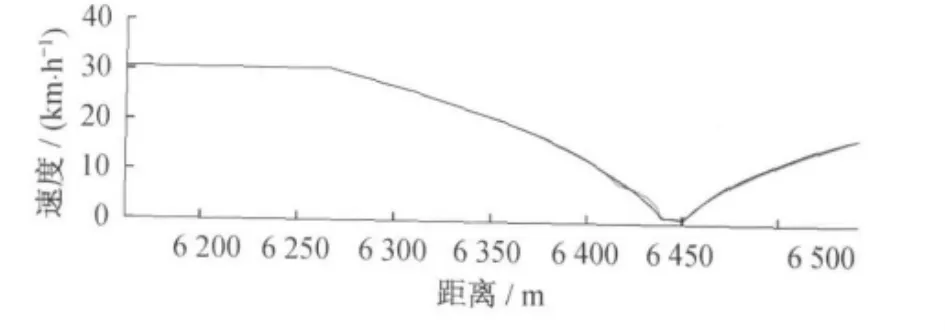
图4 列车停车制动阶段
由图5知,根据试验98.89%的列车停车在距目标停车点±0.25m范围内,而仍存在少许没有停准的情况,其产生原因是由于在站内停车阶段,测速测距产生较大误差,超出常规可调误差范围,对精确停车造成较大影响,使得最终未在停车范围内停车。针对这一情况,系统加入了列车未进入停车范围停车的对策,若列车提前停车则以低牵引档位重新使列车前行再停车,若列车超出停车范围,则使列车处于后退工况,低档牵引倒退再停车。
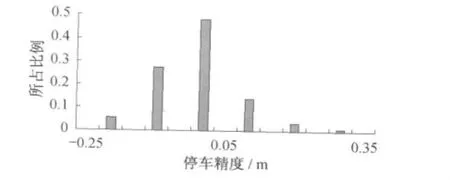
图5 停车精度柱状图
3.2.4 列车准时性分析
设列车运行准时性为规定运行时间误差±10s。经千次试验,准点率为96.04%,列车运行准点误差为E(x)==5.22s,标准差为σ(x)==E{[|x|-E(x)]2}=3.145。
由图6知,由于系统误差的存在,控制算法以信标为分割点进行控制,不可避免地与运行模式曲线存在不同的控制策略,故存在一定的运行时间偏差。由于运行模式曲线换挡位置与本系统的换挡位置差距较大,导致几例试验运行时间误差超过±10s。

图6 准时性柱状图
4 结语
本文的ATO速度控制器参考运行模式曲线,通过预测和灰色控制决策下一周期的列车操纵档位,输出给车辆接口进行速度控制。本仿真系统考虑了车辆模型传输给速度控制器的列车速度位置的误差存在、牵引或制动力的逐渐施加、列车空转打滑情况的存在等因素,大大提高了研究价值以及对现场应用的参考价值。
ATO系统在工程应用中还需要考虑车轮状况、线路湿滑、风速等因素对速度控制的影响,这也是有待今后进一步研究的方向。
[1]唐涛,黄良骥.列车自动驾驶系统控制算法综述[J].铁道学报,2003,25(3):98.
[2]黄磊,唐涛.灰色控制在城轨列车自动驾驶系统的应用研究[J].中国科技信息,2008(2):79.
[3]吴亚娟,王强.地铁列车驾驶的模糊控制技术[J].城市轨道交通研究,2000(8):30.
[4]李玉生,侯忠生.基于遗传算法的列车节能控制研究[J].系统仿真学报,2007,2(19):384.
[5]邓聚龙.灰色系统基本方法[M].2版.武汉:华中科技大学出版社,2005.
