含假人模型的跨坐式单轨车辆碰撞安全仿真分析

杜子学 徐道雷 张晓旭

（重庆交通大学轨道交通研究院，400074，重庆∥第一作者，教授）

近年来，跨坐式单轨交通以其线路占地小、噪声低、建设投资费用较低以及完成的运量在公共交通中的比例也越来越大等优越性，在国内多个城市先后建成。其车辆安全的重要性就越来越不容忽视。因此车体的碰撞安全性研究已成为轨道交通车辆设计的重要研究课题。国外已经开展了城轨车辆碰撞仿真技术以及列车的被动防护性的研究，并进行了单车和两车的碰撞试验。随着显式有限元技术的发展以及高性能计算机软、硬件资源的出现，应用计算机数值方法进行车体的碰撞模拟，也成为国内研究城市轨道车辆安全性能的主要手段，但是含假人模型的城市轨道车辆碰撞安全仿真还处于起步阶段。本文将探索模拟含有假人模型的跨坐式单轨车辆在一定初速度下与固定刚性墙的正面碰撞过程。

1 显式有限元算法

机车车辆碰撞接触过程包含了接触体系在运动和变形中所表现的几何非线性、材料非线性和接触摩擦的边界非线性，其物理本质又决定了其仿真只能采用小的时间步长，否则就会带来收敛性问题或过大的计算误差。因此城市轨道车辆碰撞采用显式仿真算法，即采用中心差分法［1］。

将碰撞过程时间域［0，T］划分成时间步Δtn（n＝1，2，…，nTS）。nTS为时间步的数量。设tn和dn＝dn（tn）分别表示第时间步的时间和位移。定义时间增量为：

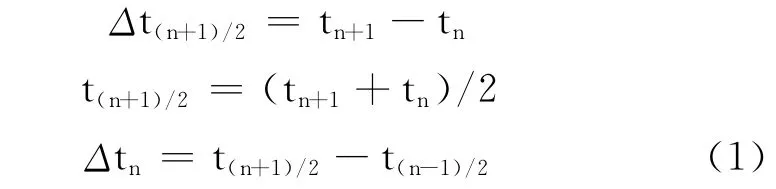
速度的中心差分公式为：

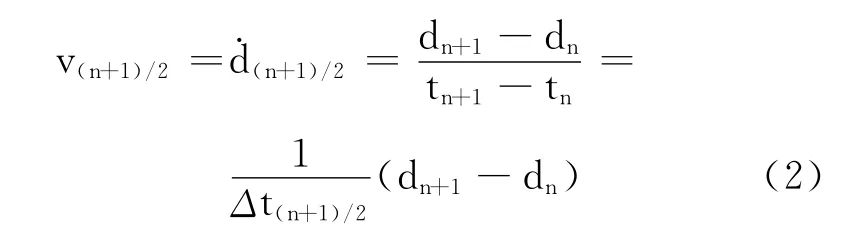
重新安排式（2）中各项，可以将差分公式转化为积分公式：

加速度和相应的积分公式为：

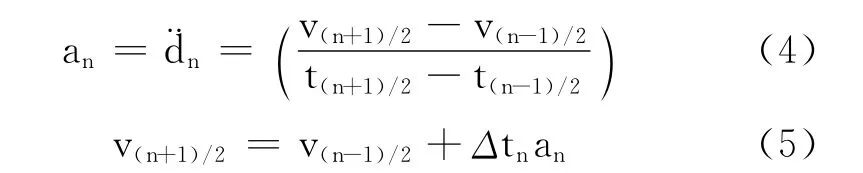
将式（1）和式（2）代入式（4），得到直接由位移的形式表示的加速度

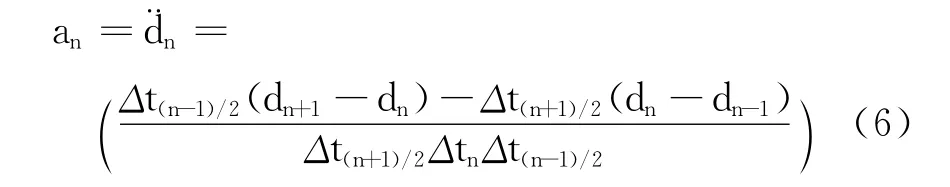
碰撞运动方程的时间积分公式可表示为：

式中：

M——质量矩阵；

fext，fint——分别是外部节点力和内部节点力（内、外部节点力都是节点位移和时间的函数）。

将式（7）代入（5），得到：

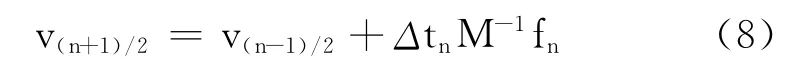
设碰撞过程已知的边界条件为：

在已知的边界条件下，位移dn已知，顺序地运算应变—位移方程、本构方程和节点力方程，可以确定节点力fn。这样式（8）中的右侧项全部已知，可以得到v（n＋1）／2，然后由式（3）可确定位移dn＋1。依次类推，可以达到碰撞过程整个时间域的位移，从而得到应变和应力。

2 含假人模型的跨坐式单轨车辆车体碰撞仿真有限元建模

2.1 有限元模型建立

跨坐式单轨车辆采用铝合金刚体材料，如A6N01S－T5、A7N01S－T5、A5083P－0和 A5083S－H112等铝型材。在有限元前处理软件Hypermesh中，车体各板梁采用板壳单元进行模拟。车体的两端是能量吸收结构，在划分网格时，车体两端的单元划分一般较密。单元以四节点四边形板壳单元为主，辅以三角形单元划分有限元网格。车体上的设备、管线、门窗等采用质量单元模拟，质量单元位置与实际结构中设备位置相同。

考虑到车轮与轨道的摩擦及后面车辆对头车的影响，模型中又添加了简化的转向架及中车模型。所采用的人体模型为完全基于试验的HybridⅢ50th型假人［2］。模拟试验时假人模型佩带三点式安全带，同时限制驾驶员的腰部和上半身。建立的车体有限元模型（含假人模型）如图1所示。

图1 含假人模型的跨坐式单轨车辆前两节车体有限元模型

2.2 焊接及接触模拟

综合考虑软硬件条件，对零件焊接的处理采用刚性连接spotweld为主，头车与中车的连接处采用springs来模拟。在本模型中并没有考虑碰撞过程中焊点的断裂失效和螺栓受剪切力断开的情况。

跨坐式单轨车辆车体正面碰撞有限元模型定义了3个接触对。首先定义的是车体总体单面的自接触，用于所有车辆部件可能发生的接触检测。第二个接触为车体前端与刚性墙的接触，并考虑摩擦，摩擦系数取0.25，其中所用的算法是主从面法。第三个接触是轮对与轨道的面接触。另外，假人模型接触算法采用了自动单面滑移接触算法，这种算法是罚函数接触算法中的一种［3］。

3 初速度42.43km／h下的跨坐式单轨车体正面碰撞仿真分析

跨坐式单轨车辆运行最高速度一般为60～80 km／h。根据英国标准GM／RT 2100，选择60km／h作为可能的目标速度［4］。由于计算模型中刚性墙固定，由动量定理和能量守恒定律可知，在机车车体塑性变形吸收同样能量的情况下，机车与同质量静止机车碰撞速度，与机车与固定刚性墙碰撞速度存在倍的关系［5］。即跨坐式单轨车辆与固定刚性墙正面碰撞速度取为v＝60／km／h＝42.43km／h。通过LS－DYNA求解器计算正面碰撞前150ms的过程。

3.1 跨坐式单轨车体正面碰撞仿真分析

3.1.1 车体骨架的变形分析

以初速度为42.43km／h的跨坐式单轨车辆车体与固定刚性墙发生正面碰撞，车体的变形历程如图2所示。

从图2中可以看出：从开始到碰撞3ms内，车体和刚性墙并未发生碰撞，从3ms开始，车头收到刚性墙的撞击，变形逐渐增加，直至65ms，此时变形最大值为232.7mm，其后的时间里，车头的变形保持不变，剩余能量经由地板、车体骨架等传至车体后部以及中车车厢，实现了能量的分散。如图3所示，整车骨架的碰撞变形区主要集中在头车前部，跨坐式单轨车体的司机室、左右侧墙、车顶及底架的前端在碰撞过程中产生了明显的塑性变形。车体后端由于第二节车的撞击发生的变形，此时车钩吸能达到最大，车钩完全实现了塑性变形。第二节车辆前端发生很小的塑性变形，这说明以这种速度与其它车辆撞击，对第二节车辆车也会产生影响。

图2 车体变形的时间历程图

图3 在t＝150ms时一位端墙变形情况

3.1.2 车体变形速度随时间变化分析

从变形速度随时间变化曲线图4中可以看出，随着撞击的开始，变形速度也逐渐增加，在12ms时达到最大值，约为7.56m／s，随后一直下降直至0，可以发现，变形速度仍在继续下降，出现了负值，这是因为材料本身的性能，在受到撞击之后，会出现一定回弹。从图4中还可以发现，变形速度的增加和回落都非常快，这说明车体的撞击比较剧烈，对于人体的损伤是一个比较大的隐患。

图4 车体变形速度－时间曲线

3.1.3 碰撞能量分析

从总动能随时间变化曲线图5得出，头车的初始动能为3 469kJ，碰撞完成后的末动能为962kJ，故头车的车体在撞击过程中耗散的总动能为2 507kJ。

图5 能量－时间曲线

另外，沙漏能只有28.6kJ，占总能量的0.8%，一般仿真要求沙漏能占总能量的比例小于5%。同时，能量总和大于初始总能量，这是因为在碰撞过程中，产生了一定的非法能量；但是该能量所占的比例很小，因此计算结果可信。

3.2 人体响应情况及损伤情况

目前我国轨道车辆还没有明确的碰撞法规要求，考虑到其碰撞形式以及乘员损伤形态，本文参照美国道路交通安全局（NHTSA）制定的美国机动车安全法规的损伤标准，使用头部损伤和胸部压缩量进行评估。其标准分别为头部损伤不超过700，胸部压缩量小于50mm［6］。

含人体模型的整车在130ms时仿真的变形过程如图6所示。碰撞开始20ms后，车辆有一定的变形，人体由于惯性力作用向前移动。在60ms时，人体响应如图（b），人体头部下倾有所增加，腿也开始弯曲。在115ms时，人体的响应如图（c），人体蜷曲现象更加严重，在130ms时，人体的响应如图（d），人体的腰部、胸部、颈部、腿部弯曲有所好转，发生回弹现象。

根据仿真分析计算得到的假人损伤值如图7所示。

从图7中可以看到，头部加速度仅为670m／s2，计算得到的人体头部HIC值为562，胸部压缩量为38mm，人体各损伤值距离法规阀值都还有一定的距离，证明了该车的结构安全性较高。

图6 人体的响应情况

图7 人体损伤值

4 结语

利用有限元软件LS－DYNA，通过计算机模拟了含有假人模型的跨坐式单轨车辆在初速度为42.43 km／h下与固定刚性墙的正面碰撞过程；车体骨架变形结果说明车体具有较好的耐撞性能。同时还得出碰撞过程中假人的响应与伤害程度，即：假人头部HIC值为562mm，胸部压缩量为38mm，人体损伤低于损伤标准，车辆结构安全性也符合要求。本研究对跨坐式单轨车辆车体结构设计具有一定的参考价值。

［1］董黎生，雷成.基于显示有限元的机车碰撞模型研究［J］.内燃机车，2008（7）：6.

［2］赵广耀，樊新华.车辆碰撞计算机模拟分析与评价［J］.东北大学学报，2008（7）：1020.

［3］郝连山.ANSYS12.0／LS－DYNA非线性有限元分析［M］.北京：机械工业出版社，2010.

［4］杜子学，张晓旭.跨坐式单轨车辆的耐碰撞性设计［J］.铁道机车车辆，2010，30（50）：69.