过渡金属配合物磁化率的测定与分析*

2013-09-25师唯徐娜王庆伦杨光明

大学化学 2013年1期

师唯徐娜王庆伦杨光明

(南开大学化学学院天津 300071)

综合化学实验是把化学的基础理论知识、实验操作技能及数据分析讨论等加以整合归纳的一种实验教学形式。该实验课程的教学目的是培养学生运用化学的理论知识和实验技能解决实际问题的能力，进而激发学生自主学习和创造性研究的积极性[1]。

近几十年来，由于晶体场理论在讨论过渡金属配合物的光学、磁学、动力学和热力学稳定性等物理化学性质时十分有效而被广大化学工作者所研究和应用，并已成为中级/高级无机化学课程中的主要内容之一。然而，该部分内容的理论性较强，学生学习时常感到枯燥难懂。如能开设相关的实验课程，将理论与实验结合起来不失为一种有效的尝试。目前，在一些大学开设的综合化学实验中，涉及晶体场理论的相关实验较少。作者结合所在高校的实验条件，设计了一个使用晶体场理论解释配合物基本磁-构关系的综合化学实验。实验中采用两种不同的合成方法制备出具有不同配位环境的Ni(Ⅱ)配合物，并对其单晶结构以及室温磁化率进行了测量，在此基础上使用晶体场理论对实验结果进行分析。通过本实验，学生不仅可以了解分子磁性的相关基础知识，还能掌握过渡金属配合物的常见合成方法、晶体结构和磁化率的测试手段，并应用晶体场理论对相应的磁现象进行初步解释。该综合实验有助于增强学生实际操作和理论分析的综合能力。

1 实验目的

(1) 掌握过渡金属配合物的基本合成方法。

(2) 掌握磁化率的意义及其与物质结构的关系。

(3) 学会测量配合物室温磁化率的方法。

(4) 应用晶体场理论对相应的磁现象进行初步解释。

2 实验原理

磁性是物质的基本性质之一，与物质的内部结构有密切的关系，所以测定物质的磁性是研究物质结构的基本方法之一。在化学上常用摩尔磁化率χM来表示物质的磁性。摩尔磁化率χM=∂M/∂H，式中M为物质的摩尔磁化强度，H为磁场强度，摩尔磁化率χM是一个张量。如果样品为各向同性时，则摩尔磁化率χM是一个标量。当外场不太强时，摩尔磁化率χM是不依赖于外磁场的物理量，即1mol物质在单位外场作用下所产生的磁化强度，可用下式计算：

在研究物质的磁性时，也常使用有效磁矩μeff来进行分析，其与摩尔磁化率的关系为：

式中T为绝对温度。根据Pauli原理，同一轨道上成对电子的自旋磁矩相反，互相抵消，只有未成对电子才能产生磁矩。有效磁矩的大小可由下式表示：

式中J为未成对电子的总角动量量子数，J=L+S，S为总自旋角动量，L为总轨道角动量。

在大多数第一过渡系列金属配合物中，由于轨道角动量被晶体场全部或部分淬灭，也就是轨道对磁矩的贡献要比自旋的贡献小得多，因此对于大多数过渡金属(除六配位的Co2+，Mn3+等外)，有效磁矩可用下式表示：

因此，当通过实验测得磁化强度后,可求得摩尔磁化率和有效磁矩，进而计算出未成对电子数n。在很多实际情况中，计算值和实验值会有一定的差距，这主要是因为轨道磁矩被忽略的缘故。

使用晶体场理论对配合物进行磁-构分析是现代配位化学的基本内容之一。晶体场理论是在离子模型的基础上发展起来的理论分析方法，它不再像离子模型那样把配合物的配体和中心离子看成是无结构实体，而是考虑由于配体所产生的电场对中心离子内部结构的影响。配体用点电荷或点偶极子表示，即假定作用在中心离子电子上的电场是由点电荷或点偶极子产生的。研究证明，在处理过渡金属离子配合物时讨论电场，只要考虑处在中心离子周围的相邻组分就能达到很好的近似效果，离得更远的晶格组分对电场的贡献可以忽略，即由直接与中心离子配位的原子的几何排布所形成的对称性是最重要的[2]。在形成配合物时，中心离子受到晶体场的影响，它的电子状态会发生改变，其电子组态也会随之发生改变。有些组态只被晶体场移动，而另一些则被分裂。这时中心离子的电子填充模式也会发生变化，并因而导致配合物的宏观磁性质因晶体场对称性的不同而改变。

本实验中，我们将对合成的两个过渡金属镍(Ⅱ)配合物N,N′-二水杨乙二亚胺基合镍(Ⅱ)(1)和二(N-异丙基水杨醛亚胺基)合镍(Ⅱ)(2)进行室温磁化率的测量，结合单晶结构分析，使用晶体场理论初步探讨其电子结构与磁性之间的关系[3-6]。

配合物1的合成反应方程式如下：

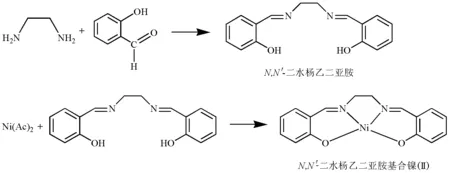
配合物2的合成反应方程式如下：

3 仪器与试剂

磁天平(或者振动磁强计、超导量子干涉SQUID磁强计)，X射线单晶衍射仪，体式连续变倍显微镜，X射线粉末衍射仪，元素分析仪，烧杯，圆底烧瓶，回流冷凝管，吸滤瓶，布氏漏斗等。

四水合乙酸镍，水杨醛，乙二胺，异丙胺，甲醇，乙醇，乙醚。以上试剂均为分析纯。

4 实验步骤

4.1 镍(Ⅱ)配合物的合成[7-8]

4.1.1 N,N′-二水杨乙二亚胺基合镍(Ⅱ)(1) 的合成

向100mL圆底烧瓶中依次加入12.2g水杨醛、20mL甲醇和3.0g乙二胺，搅拌加热回流1小时，冷却至室温，有固体析出，减压过滤，分别用甲醇和乙醚各洗涤产品两次后得到淡黄色固体，再用150mL甲醇重结晶，得到亮黄色晶体，在烘箱中65℃干燥30分钟，冷却后称量，得到N,N′-二水杨乙二亚胺配体，产量11.5g，产率86%。将得到的配体与等物质的量的四水合乙酸镍放入圆底烧瓶中，加入50mL乙醇，搅拌加热回流1小时，冷却，减压过滤得到棕红色晶状产物。用乙醇洗涤3次，干燥，称量。产量9.9g，产率71%。

4.1.2 二(N-异丙基水杨醛亚胺基)合镍(Ⅱ)(2)的合成

4.2 单晶结构测试[9]

配合物1和2的产品均为纯净晶体，在20～50倍体式显微镜下挑选质量好的单晶样品。适合X射线单晶衍射测试的晶体需形状规整、透明、无裂纹、表面干净，且尺寸与所用单晶衍射仪的X射线光柱直径匹配。用AB胶将大小合适的一颗单晶粘在载晶台的玻璃丝顶部，将载晶台固定在X射线单晶衍射仪内，把晶体调节到测角器中心上。首先通过预实验获得若干张衍射图像，经过计算机寻峰并指标化其中的衍射点，进而初步决定晶胞参数和取向矩阵。一般情况下，按照软件的缺省设置可以满足晶体衍射数据的收集，或者根据经验设置出收集衍射数据的最优化条件后，开始正式收集完整的衍射数据。数据收集完毕后经过仪器自带的数据还原程序对衍射数据进行还原，再使用结构解析/精修软件(如Shelxtl或Olex2等)解析并精修单晶结构，得到两个样品的单晶结构数据。

4.3 样品纯度表征

使用元素分析仪测试了配合物1和2的C、H、N的含量。配合物1(C16H14N2NiO2)的理论值(%)为：C 59.13，H 4.34，N 8.62；测量值(%)为：C 59.52，H 4.79，N 8.71。配合物2(C20H24N2NiO2)的理论值(%)为：C 62.70，H 6.31，N 7.31；测量值(%)为：C 63.04，H 6.78，N 7.24。该分析结果表明两个样品的化学组成纯度较高。

配合物1和2的X射线粉末衍射谱图与用单晶数据获得的模拟谱相一致(图1)，表明配合物1和2样品相纯度较高。

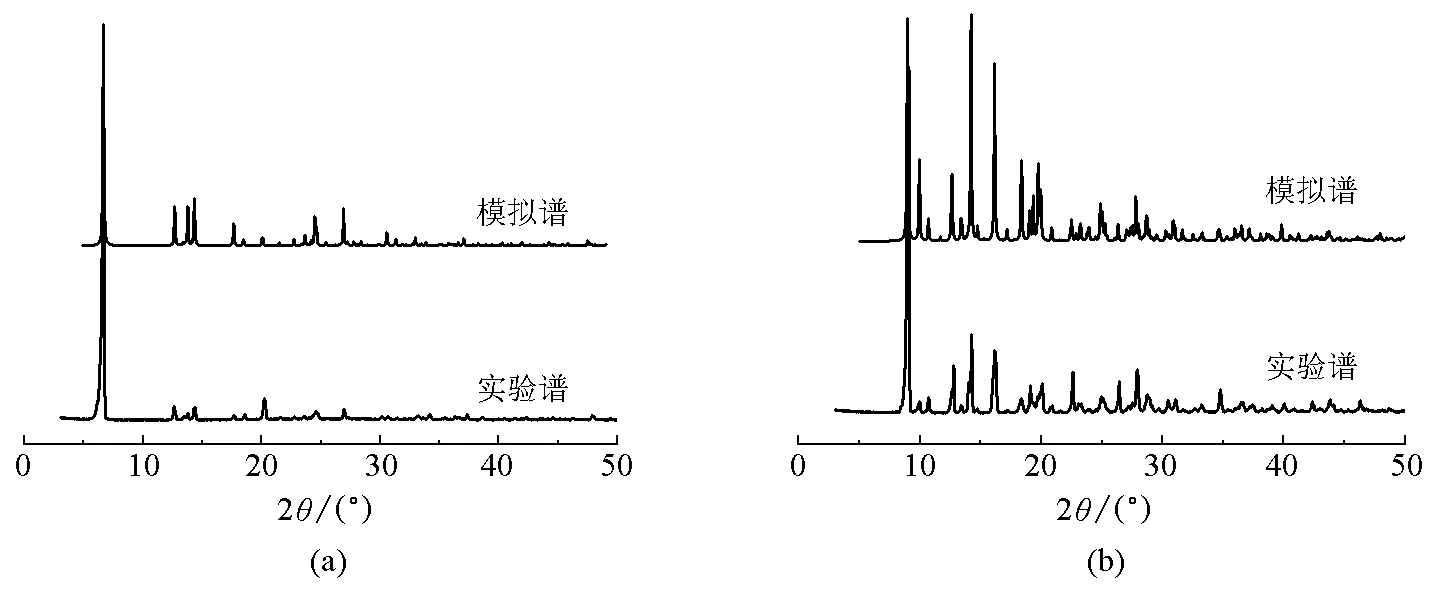
图1 配合物的X射线粉末衍射图(a) 配合物1；(b) 配合物2

4.4 磁性测量[10]

4.4.1 开机与调试

打开MB-1A磁天平，预热。将探头置于电磁铁的中心架上，调节特斯拉计的调零电位器，使其输出显示为零；调节探头最佳位置；确定样品管内应装样品的高度。

4.4.2 空样品管的测量

取一支清洁干燥的空样品管悬挂在磁天平的挂钩上，使样品管正好与磁极中心线平齐，不可与磁极接触。准确称量零外场(H0)下空样品管的质量m1(H0)；调节电流调节电位器，使特斯拉计显示0.300T(特斯拉)，迅速称得m1(H1)；逐渐增大电流，使特斯拉计显示0.350T，称得m1(H2)；将电流略微增大后再降至0.350T，称得m2(H2)；将电流降至0.300T，称得m2(H1)；最后将电流调节至特斯拉计显示0.000T，称得m2(H0)。这样调节电流由小到大再由大到小的测定方法是为了抵消实验时磁场剩磁的影响。

式中Δm1(H1)=m1(H1)-m1(H0)；Δm2(H1)=m2(H1)-m2(H0)；Δm1(H2)=m1(H2)-m1(H0)；Δm2(H1)=m2(H2)-m2(H0)。

4.4.3 装样和测量

在样品管中装入研细干燥的莫尔盐(标样)，填实，按4.4.2方法将样品管置于磁天平上称量。用清理干净的同一样品管,采用相同方法分别测量配合物1和2的Δm空管+样品(H1)和Δm空管+样品(H2)。得到的3组样品数据可以分别采用直接法和标样法来计算所得配合物的磁性数据。

实验结束后，调节调压旋钮使特斯拉计显示为零，关闭电源。

除了使用磁天平进行磁性测试外，还可以根据所在学校的具体情况使用振动磁强计、SQUID磁强计等其他磁性测量仪器进行测试。在此，我们也提供了使用SQUID磁强计测量的配合物1和2的室温磁化率数据作为参考。

5 实验结果与计算

5.1 单晶结构

X射线单晶衍射测试得到的结构数据显示配合物1的化学式为C16H14N2NiO2，配合物2的化学式为C20H24N2NiO2。使用仪器自带的绘图软件或Diamond 2.0试用版软件观察这两个镍(Ⅱ)配合物的晶体结构[11-12]。Diamond具有晶体结构的绘图功能，可以在Windows操作系统下使用鼠标灵活操作，绘制出各种分子图、堆积图和拓扑结构图等。打开该软件，载入晶体数据文件(*.cif或*.res)；点击“Molecule”生成分子结构图，点击“Adjust”调整图形大小，点击“Rotation X/Y”调整分子显示的角度和方位；可通过鼠标单击选择某个或多个原子和化学键，右键用“Delete”删除多余部分，只留下一个中心金属离子以及与其配位的配体分子，再点击“Adjust”调整图形；可在原子列表中选择所有的H原子并删除，调节其他原子的颜色以及化学键的颜色和尺寸；点击“Objects/Text…”标出原子标号。还可通过一些更复杂的操作得到键长和键角等数据。结构图画好后,可以通过“Edit/Copy”操作，粘贴到文档中。如图2所示，配合物1和2中的Ni(Ⅱ)离子分别处于平面四边形和正四面体配位环境中。

图2 配合物的单晶结构图(a) 配合物1；(b) 配合物2(所有氢原子已省略)

以上步骤可根据所在学校的具体情况选用。晶体结构数据也可从网络获得。

5.2 磁性

5.2.1 磁天平测量结果

表1 采用直接法得到的配合物磁性测量结果

μB=9.27×10-24J·T-1,下同。

表2 采用标样(莫尔盐)法得到的配合物磁性测量结果

5.2.2 SQUID磁强计测量结果

使用Origin软件绘制磁化率测量图，摩尔磁化率可由图中斜率得到。

表3 SQUID磁强计对配合物磁性的测量结果

5.3 讨论

由单晶结构分析可知，配合物1的中心Ni(Ⅱ)离子处于平面四方形的配位环境中。根据晶体场理论，5个d轨道在平面四方形场中会分裂成4组，分别属于eg，a1g，b2g和b1g不可约表示，其中b1g轨道能量最高，eg轨道能量最低，如图3(a)所示。根据能量最低原理和Pauli不相容原理，Ni(Ⅱ)离子的8个d电子填充到能量较低的4个轨道当中，其成单电子数为0，因而理论有效磁矩为0。配合物2的中心Ni(Ⅱ)离子的配位构型为正四面体，5个d轨道分裂成两组，分别属于e和t2不可约表示，其中t2轨道能量较高，e轨道能量较低。同样根据能量最低原理和Pauli不相容原理，Ni(Ⅱ)离子的4个d电子填入能量较低的e轨道，另外4个d电子填入能量较高的t2轨道，如图3(b)所示，其成单电子数为2，因而理论有效磁矩值为2.828μB。以上分析与磁化率的测量结果一致。

图3 d8电子组态在平面四方形(a)和四面体(b)晶体场下的电子填充图

6 结语

本文在实验目的、实验步骤和测量方法，以及专业知识的运用等方面，密切结合高校本科实验教学的实际情况，设计了一个适合于高年级本科生的综合性实验。本实验在训练学生实验动手能力的同时，使学生了解利用单晶衍射仪和磁强计等现代仪器对配合物类材料进行结构和磁性表征的基本方法，以及应用晶体场理论对磁-构关系进行基本分析，培养和锻炼了学生的实际操作和理论分析的综合能力。

参考文献

[1] 吕占霞,贺维军,高珍,等.大学化学,2011,26(1):14

[2] Schläfer H L,Gliemann G.配体场理论基本原理.曾成,王国雄,朱忠和,等译.南京:江苏科学技术出版社,1982

[3] Kahn O.Molecular Magnetism.New York:VCH Publishers,1993

[4] Carlin R L,Van Duyneveldt A J.Magnetic Properties of Transition Metal Compounds.New York:Springer-Verlag,1977

[5] Peddie W.Molecular Magnetism.London:Edward Arnold & Co,1929

[6] 洪茂椿,陈荣,梁文平.21世纪的无机化学.北京:科学出版社,2005

[7] Kondo M,Nabari K,Horiba T,etal.InorgChemCommun,2003,6(2):154

[8] 吴世华,邱晓航,王庆伦.无机化学实验.北京:科学出版社,2010

[9] 陈小明,蔡继文.单晶结构分析的原理与实践.北京:科学出版社,2003

[10] 王秋长,赵鸿喜,张守民,等.基础化学实验.北京:科学出版社,2003

[11] Siegler M A,Lutz M.CrystGrowth&Des,2009,9(2):1195