关于理想气体混合熵变的讨论
2013-09-25岳凡陈华梅孙都成
岳凡 陈华梅 孙都成
(新疆大学化学化工学院 新疆乌鲁木齐 830046)
物理化学是大学化学专业学生必修的四大专业基础课之一,而化学热力学则是物理化学中非常重要的内容之一。化学热力学理论性强,数学处理比较复杂,公式较多,而且公式的使用限制条件也较多,学生不易掌握。因此,在物理化学教学中,可尽量通过比较形象化的方式使学生理解,并适当地将理论与实际相联系,使学生体会到学习物理化学的乐趣,从而达到在有限的教学课时内使学生对本课程内容更好掌握的目的[1]。
在文献[2]第3章第87~88页中,讨论了理想气体的等温等容混合熵变,这是一个比较容易出错和容易混淆的概念。
原文提出,对于相同理想气体的等温等容混合,如图1所示。
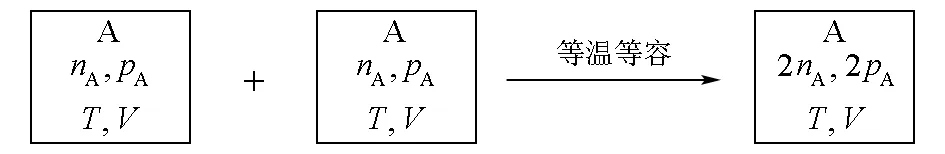
图1 相同理想气体等温等容混合
由于是相同分子的混合,每个分子在混合后的活动范围缩小一半,相当于体积缩小一半,气体被压缩,所以混合后熵减少,其熵变为:
不同理想气体的等温等容混合如图2所示。

图2 不同理想气体等温等容混合
因为是理想气体的等温物理变化过程,所以ΔmixU=0。终态压力p=pA+pB,有:
Δ(pV)=pV-(pAV+pBV)=0
所以有:
ΔmixH=ΔmixU+Δ(pV)=0
对于不做非膨胀功的等容可逆过程,QR=ΔmixU=0,所以
ΔmixS=0
因为是不同理想气体的混合,根据理想气体的微观模型,气体分子之间的相互作用力可以忽略不计,分子本身的体积也可以忽略,所以混合前后两种不同分子的活动范围都没有发生变化,混合时没有热效应,所以也就没有熵的变化。
关于这点,学生学习时会感到很迷惑,其一是,书中对第二种情况推导所得的ΔmixU=0以及ΔmixH=0在对第一种情况似乎同样适用,当然这一步事实上是正确的。那么问题就在下一步,“对于不做非膨胀功的等容可逆过程,QR=ΔmixU=0,所以ΔmixS=0。”这段话,应该只适用于第二种情况,而对相同气体的这一过程来说,这段话并不适用,学生对于这一点有疑义,由于这种怀疑心理而产生的不确定感,导致学生认为物理化学课程学习有些不可掌握,从而产生一定程度的陌生感及厌学情绪。为克服学生的这些负面感觉,在教学过程中可采用学生较熟悉的推导过程来证明这一结论;另外,由于形象化教学更易理解,更易记忆,在教学过程中也被尝试采用。
首先,用学生比较熟悉的两个过程来模拟这一过程,从而证明这一结论的正确性。
对于相同的理想气体,先设计第一步,将两等压等体积的相同理想气体,经一等温等压过程,合并为两体积的理想气体,如图3所示。

图3 相同理想气体等温等压混合
学生很容易从这一过程得出熵变为0的结论。
第二步,将这一气体等温压缩至体积为原来的一半,即上述过程的终态。在这一过程中,由于是等温变化,所以ΔU=0,QR=-WR。对于等温可逆过程,有:
所以有:
与课本结果相同。
对于不相同的理想气体,也经过同一过程(图4)。

图4 不同理想气体等温等压混合
在第一步时,由于是不同气体发生混合,则混合熵可根据前面第2节的结论,得计算结果为:
然后将这一混合气体等温压缩为原来的一半,这时,根据与上面同样的理由,可得此时的熵变为:
将两式相加,可得这一过程的总熵变为0。
通过以上过程的证明,一方面使学生对该问题有了可掌握感,另一方面,也是对以前教学内容的一种复习巩固。
另外,为形象地解释这种熵变产生的原因,可由熵的玻尔兹曼定义[2]S=klnΩ(Ω为微观状态数)对这一过程进行讨论。
在相同气体分子进行混合时,为简化讨论,将其设为一个小球在两个格子里的排列,对于两体积气体混合前后的过程,可以简化表示如图5。

图5 相同理想气体等温等容混合简化统计表达
此时总的微观状态数为3,小于前两者分开时总的微观状态数4。经观察之后,学生可发现,在A1+A2状态时,第3种状态由于A1与A2的不可区分性,由两种状态变成了一种状态,就是由于这一原因,造成同一理想气体在等温混合时产生了熵减。
对于不同理想气体等温等容混合时,其统计学图像简化如图6。此时,混合前后微观状态数不变。
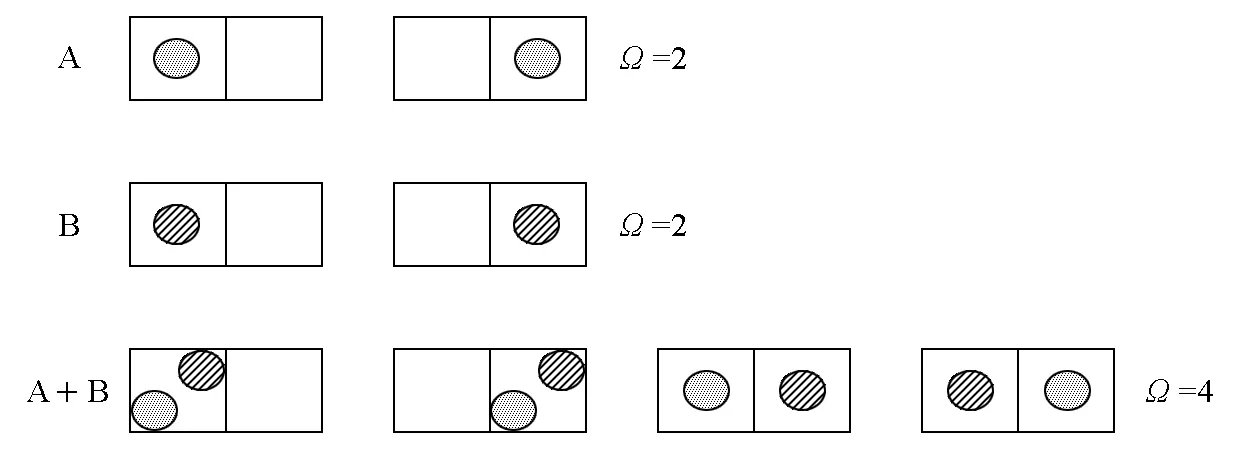
图6 不同理想气体等温等容混合简化统计表达
从统计角度可清楚地揭示两种混合状态物理图像的差别。在A+B中,第3种状态与第4种状态是不同的,表明此时A在左与A在右有区别,就好像A+B之后,A仍然独立地占有两个格子;所以,对于A来说,这是一个等容过程。而在A1+A2中,这两种状态变成不可区分的一个状态,此时A1在左与A1在右没有区别,就好像A1+A2后,A1只占据其中一个格子一样;所以,对于A1来说,这是一个体积减小了一半的非等容过程。
问题讨论到此,学生还有一个疑问,就是关于这个问题的热力学解释的实际意义。如果不能应用于解决实际问题,就纯粹是一个抽象的理论游戏,这样学生就缺乏掌握此概念的动力,认为这是一个既麻烦,又无用的章节。下面采用一个在化工生产中非常重要的反应来进行说明。
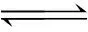
对于这个反应来说,达到平衡时,有如下关系:
ΔrG=ΔrH-TΔrS=0
对此体系加入一惰性气体,使总压增加一倍,而体积保持不变。这就相当于上面讨论的不同理想气体等温等容混合。因为是理想气体等温混合过程,所以没有混合热,此反应的ΔrH不变。对于O2(g)及CO(g)来说,由上面结论可知,两物质的熵也不改变,所以ΔrG仍然等于0,平衡不发生改变,与用平衡常数讨论的结果相同。而当加入反应气体时,由于混合熵改变,将导致反应平衡被打破。
通过以上讨论,能使学生从多个角度来理解理想气体混合熵变这一过程,使抽象的问题具体化。通过该教学设计,不但不会加重学生的负担,反而会提高学生对不同过程熵变的计算及其推论的理解,在介绍新概念的同时,达到复习旧课程、提高记忆准确性的目的。在实施新课改的今天,我们让学生从不同的角度认识和解决同一类问题,有利于培养学生分析问题和解决问题的能力,提高学习效果。
参 考 文 献
[1] 刘瑞泉,张金萍.乌鲁木齐成人教育学院学报,1997(2):54
[2] 沈文霞.物理化学核心教程.第2版,北京:科学出版社,2009
