基于强度折减法的三维边坡稳定性与破坏机制
2013-09-22年廷凯张克利刘红帅徐海洋
年廷凯,张克利,刘红帅,徐海洋
1.大连理工大学土木水利学院/海岸和近海工程国家重点实验室,辽宁 大连 116024
2.成都理工大学地质灾害防治与地质环境保护国家重点实验室,成都 610059
3.中国地震局工程力学研究所,哈尔滨 150080
0 引言
工程边坡大多呈现三维状态,且具有独特的地质环境和几何形态特征,而二维分析往往不能真实反映边坡的实际受力状态和失稳破坏模式,因此三维分析在边坡安全性评价和加固设计中更具有实际意义。当前较为有效的三维边坡稳定性分析方法是基于强度折减技术的弹塑性有限元法,已经受到国内外学者的广泛关注和普遍认可,且开展了大量的基础性研究工作,如:边界条件对三维边坡稳定性的影响[1-5],含软弱夹层的三维边坡稳定性分析[6-7],坡顶超载条件下的三维边坡安全性评价等[7],均取得了一些很有意义的成果,但对复杂地质环境及负载条件下的三维边坡稳定性及破坏机制的研究还很少开展。基于这一现状,笔者结合典型算例,探讨边界条件、岩土强度参数、坡顶局部超载、地震荷载等因素对三维边坡稳定性及潜在滑动面的影响;在此基础上,着重研究含软弱夹层及地下水的三维复杂边坡在负载条件(坡顶局部超载与地震荷载)下的失稳破坏模式及滑动机制,以期为三维边坡稳定性评价及灾害预测提供科学依据。
1 强度折减有限元法
强度折减有限元法具有极限平衡法无法比拟的优势,计算过程中无需假定潜在滑动面的形状和位置,自动搜索潜在滑动面并确定稳定性系数,且能够得出与极限平衡法相近的安全系数和临界滑动面[8],为三维边坡稳定性数值分析提供了极大的便利。
1.1 强度折减技术
利用大型有限元程序ABAQUS[9],进行强度折减有限元计算,边坡土体采用Mohr-Coulomb破坏准则与非关联流动法则的理想弹塑性本构模型。考虑目前存在的4种主要边坡失稳判据高度一致性[10],笔者以数值迭代不收敛并结合坡面特征点位移陡增作为边坡失稳判据,即在此时的强度折减系数为边坡稳定安全系数。强度折减计算中,折减后的强度参数表达为
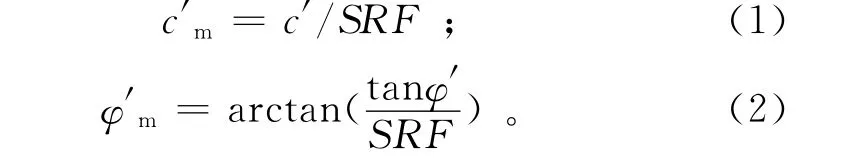
式中:c′和φ′分别是土体的实际有效黏聚力和内摩擦角;c′m和φ′m分别是土体发挥的有效黏聚力和内摩擦角;SRF为强度折减系数。强度折减计算中需满足φ-v(即摩擦角-泊松比)不等式要求[11-12]。
1.2 有限元计算模型及边界条件
数值计算的3D模型如图1所示。
3D边坡稳定性计算可根据实际情况选用3种不同的边界条件,即自由边界、半约束边界和全约束边界,具体实施见表1。为减少计算工作量,若为自由边界和全约束边界时,在Z=L/2处对称取半。
1.3 合理网格密度的选取
算例1 三维边坡几何模型如图1[6]所示,W1=W2=S=2 H,L=2 H。边坡尺寸与材料参数如下:坡比为 H∶L=1∶2,c′/(γH)=0.2,其中,坡高H=10m,重度γ=20kN/m3,土的黏聚力c′=40 kPa,φ′=10°;变形参数E=105kPa,v=0.3。考虑自由边界和半约束边界2种情况(全约束边界对称取半计算,类似半约束边界模式,故省略),采用20节点六面体单元,以5、4、3、2、1.5、1m 网格大小进行强度折减对比计算,所得强度折减系数与无量纲位移的变化曲线如图2所示,安全系数列于表2。

图1 三维边坡几何模型Fig.1 3Dslope geometry model

表1 三种边界的描述Table1 Description of the 3Dslope boundary conditions
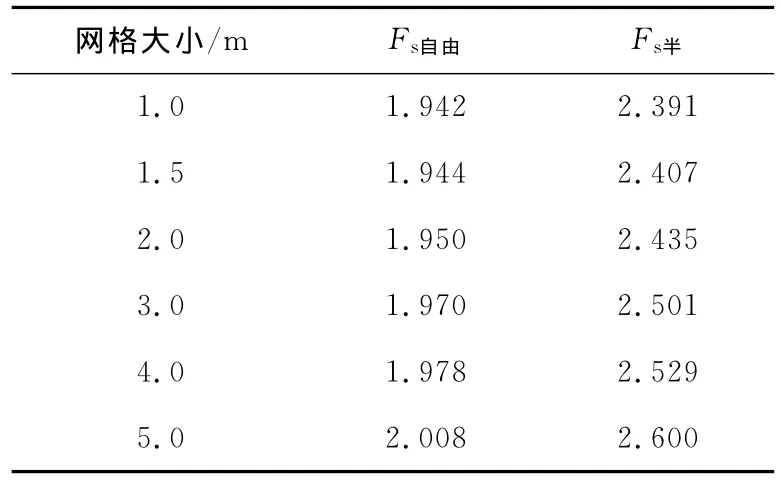
表2 网格密度对安全系数(Fs)的影响Table2 Effect of density of elements on the factor of safety
由图2可见,随着强度折减系数的增加,Mohr-Coulomb强度参数逐渐降低,当降低到某一值时,无量纲位移Eδmax/(γH2)迅速增加,进而计算不收敛,等效塑性区亦贯通为连续的滑动面,其中δmax为边坡坡面上的最大位移。进一步分析图2可见:自由边界条件下网格大小对安全系数和无量纲位移的影响相对较小,当网格小于2.0m时安全系数趋于相等;半约束边界条件下网格大小对安全系数和无量纲位移的影响相对较大,但随着网格变小对安全系数的影响逐渐减弱,当网格大小控制在1.5m以下时对安全系数的影响可忽略。
由表2亦可看出,当单元尺寸控制在1.5m以下时,其对安全系数的影响小于5%。因此在三维边坡强度折减有限元分析时,建议网格大小为1.0~1.5m(相对网格大小0.1~0.15)。
2 边坡破坏模式与机制探讨
2.1 边界条件及强度参数对潜在滑动面的影响
算例2 边坡几何形状与材料参数如图3所示,其中Z方向长度L=2 H,内摩擦角φ=20°,黏聚力c分别取25、50、100kPa。针对3种边界条件,考察不同坡比条件下黏聚力对潜在滑动面边坡安全系数的影响,所得计算结果列于表3,潜在滑动面如图4所示。
由表3可以看出:全约束边界条件下边坡稳定安全系数最大,而自由边界条件下最小;1∶1边坡安全系数远高于直立边坡,且随着黏聚力增加,前者的安全系数增长幅度也远大于后者。
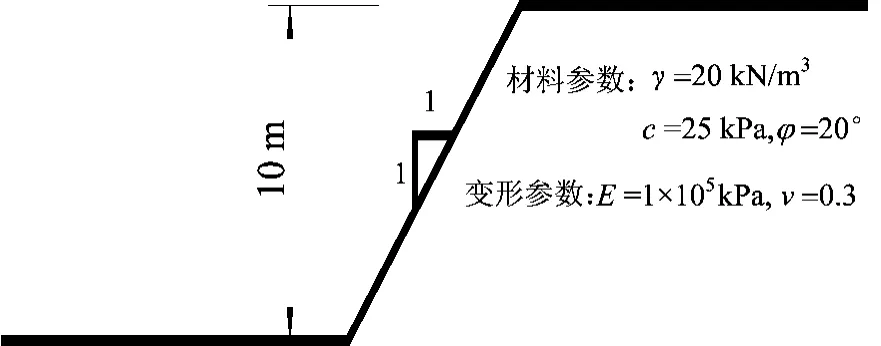
图3 三维边坡截面图Fig.3 Cross-section of 3Dslope
由图4可见,自由边界条件下随着黏聚力的增大,边坡潜在滑动面表现出如下变形破坏规律:滑坡体的剪出位置远离坡脚,滑坡后沿远离坡肩,滑坡深度加深,滑坡体积增大。对比分析,在半约束和全约束边界条件下(图略),随着黏聚力的增大亦表现为相似的变形破坏规律,但自由边界条件下上述特征更突出;当黏聚力较小时滑动面贴近坡面,接近于浅层滑动。对于直立边坡(坡比为1∶0)得到的规律与上述相同。

表3 不同条件下黏聚力对边坡安全系数的影响Table3 Fswith different boundary conditions and cohesion
2.2 负载对边坡潜在滑动面的影响
2.2.1 均布荷载对潜在滑动面的影响
采用算例2,坡顶局部受均布荷载作用(图5),荷载强度q分别取0、150、300kPa,离坡肩的距离为2m,面积2m×8m。不同约束条件下的安全系数列于表4,其中自由条件下的等效塑性应变(PEEQ)分布如图6所示。
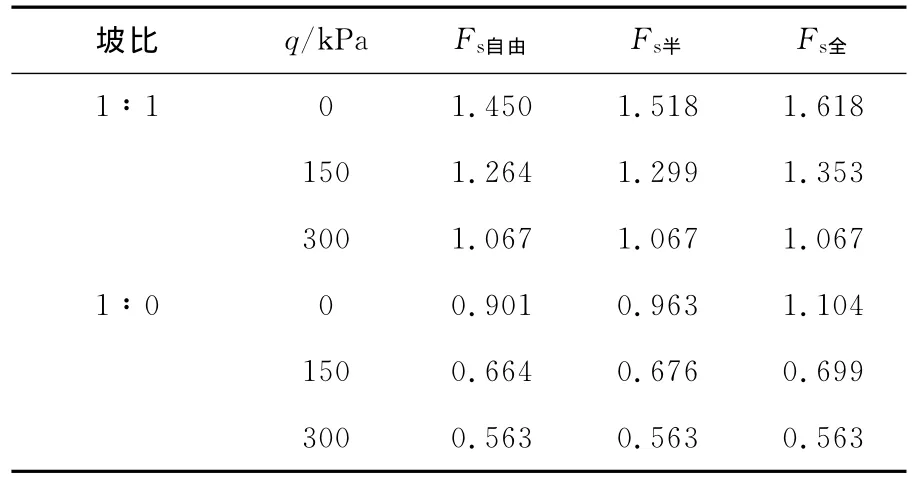
表4 不同均布荷载下边坡的安全系数Table4 Fsof the slope with different uniform loads
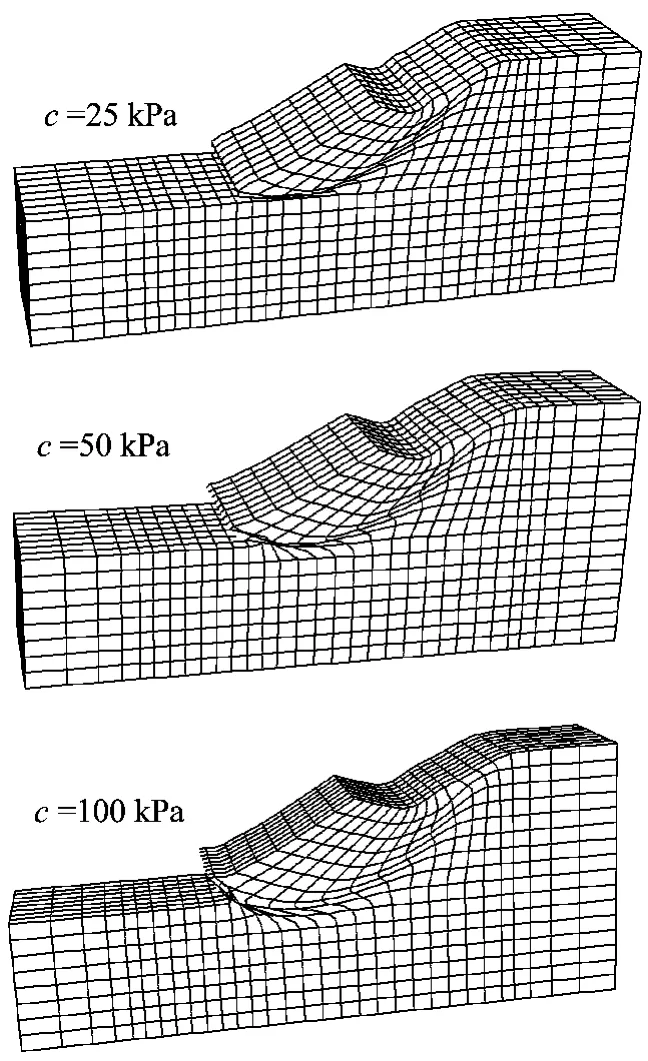
图4 自由边界条件下边坡变形破坏模式(坡比为1∶1)Fig.4 Deformed mesh of the slope (1∶1)under free boundary

图5 三维边坡截面图Fig.5 Cross-section of 3Dslope
由表4可见,不论是缓坡还是陡坡,当超载强度较低时(150kPa),边界约束条件对边坡稳定安全系数的影响明显;当超载强度较高时(300kPa),这种影响可忽略。分析图6(坡比为1∶1)可见:当均布荷载q较小时(150kPa),边坡表现为整体破坏模式,其破坏机制为由岩土体固有强度参数、边坡边界条件和均布荷载共同控制;当均布荷载较高时(300 kPa),其等效塑性应变区发生了很大变化,由大范围整体塑性变形转变为局部塑性变形,破坏模式由整体破坏转变为局部破坏,其潜在滑动面由均布超载控制为主,几乎不受边界条件影响。对于直立边坡得到的结论与上述相同。

图6 均布荷载下等效塑性应变分布(坡比为1∶1)Fig.6 Distribution of equivalent plastic strain with different uniform load(slope ratio 1∶1)
2.2.2 地震荷载对边坡潜在滑动面的影响
同算例1,地震加速度特征值取ah=0.2g,仍采用3种边界约束条件计算安全系数和潜在滑动面。对于V∶H=1∶2边坡,其结果分别为Fs=1.355,1.499和1.696(不考虑地震力时 Fs=1.944、2.407、2.600),相应的潜在滑动面如图7所示;对于直立边坡,Fs=0.803,0.863和0.962(不考虑地震力时Fs=0.964、1.126、1.273)。
通过比较图7a,b可见,地震荷载作用下边坡的潜在滑动面后沿远离坡肩,滑动深度略微变浅,边坡整体稳定性显著下降。
2.3 含软弱夹层和地下水的复杂边坡破坏分析

图7 地震荷载下边坡变形破坏模式Fig.7 Deformed mesh of slope under earthquake load
算例3 该边坡考虑4种工况:一是均质边坡;二是假设该边坡内含有软弱夹层;三是假设为均质边坡,考虑地下水的影响;四是假设边坡含有软弱夹层和地下水。具体的边坡几何形状如图8所示,考虑地下水时的渗流场分布如图9。该算例首先被Zhang[1]所采用,随后被许多学者广泛引用来校核三维边坡稳定性分析方法的正确性[3,13-14]。Zhang假定滑裂面为对称的椭球面,即滑裂面在XOY平面内是圆弧,在z轴方向有椭圆面生成。

图8 算例3三维边坡截面图Fig.8 Cross-section of 3Dslope in Example 3
工况1 -4采用半约束边界条件,计算得到的安全系数与文献结果对比列于表5。由表5可见,本文解与其他解非常接近,相对误差在5%左右。
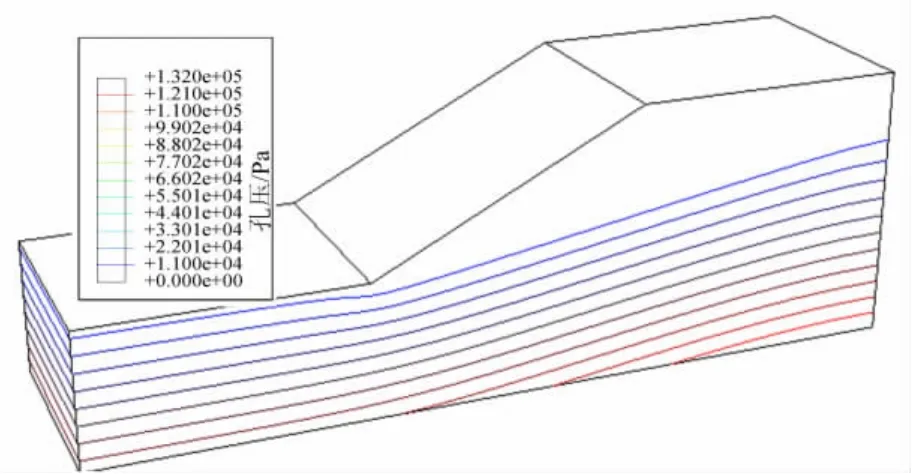
图9 考虑地下水时的渗流场分布Fig.9 Distribution of seepage contours

表5 三维边坡安全系数对比Table5 Comparison of Fsof 3Dslope
图10显示了4种工况下边坡的变形网格,可见工况1和工况3的潜在滑动面呈曲面,是否为椭球曲面仍有待进一步研究;结合表5可见,考虑地下水后边坡的稳定性显著下降,且潜在滑动面加深,滑坡体体积有所增大。工况2和工况4的潜在滑动面在软弱夹层以上呈曲面,在软弱夹层处被截断,沿夹层呈平面伸展至剪出口。
2.4 负载条件下复杂边坡的破坏模式分析
仍采用算例3,在工况1、工况2及工况3中考虑均布荷载(q=200,300kPa)和拟静力地震荷载(ah=0.2g),计算安全系数列于表6,PEEQ 分布如图11和图12所示。

表6 复杂边坡的安全系数Table6 Fsof slopes under surcharge and seismic loads

图10 各工况下边坡变形图Fig.10 Deformed meshes of slopes under four cases
由表6可看出,在考虑坡顶超载和地震荷载时,地下水或软弱夹层的存在都会使边坡的稳定性安全系数明显降低。
由图11a、b及图12对比可见,在均布超载与地震荷载作用下,含软弱夹层的边坡等效塑性应变分布完全不同,其边坡破坏模式亦不同;均布超载作用下,含软弱夹层的边坡破坏是由于潜在滑坡体与相对稳定区竖向剪切和软弱夹层水平错动的联合作用结果,而地震荷载作用下该类边坡破坏归因于软弱夹层水平错动起主导作用。
3 结论
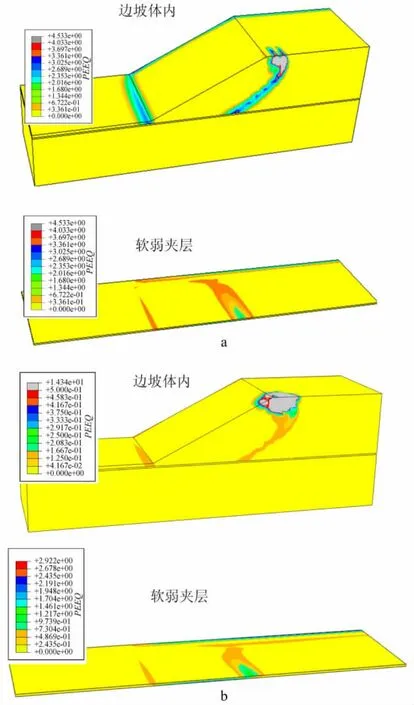
图11 均布超载下边坡等效塑性应变分布Fig.11 Distribution of equivalent plastic strain for slopes under surcharge
1)三维边坡弹塑性有限元分析时,相对网格大小对边坡稳定安全系数有一定的影响,随着网格变小计算安全系数趋于稳定;算例分析表明,相对网格大小控制为0.10~0.15时比较合理。
2)随着黏聚力增加,三维边坡潜在滑动面的剪出位置远离坡脚,滑坡后缘远离坡肩,滑坡深度加深,滑坡体积增大。边坡越缓这一特征越突出,自由边界条件下上述特征更突出。
3)边坡稳定性及潜在滑动面的剪出点、滑坡深度和滑坡后缘,与边坡土体强度、地下水分布及外荷载有着密切关系。当坡顶超载强度q较小时,边坡破坏模式由土体强度、边界约束条件和均布超载共同控制;当q较大时,以均布超载控制为主;受地震荷载作用时,边坡潜在滑动面后缘远离坡肩,滑动深度略微变浅,整体稳定性显著下降。

图12 地震荷载作用下边坡等效塑性应变分布Fig.12 Distribution of equivalent plastic strain for slopes under earthquake loads
4)含软弱夹层的三维边坡,其潜在滑动面呈折线型;当受超载作用时其破坏模式和滑动机制与地震作用下截然不同:前者归于潜在滑坡体与相对稳定区的竖向剪切和软弱夹层的水平错动联合作用结果,而后者归于软弱夹层水平错动起主导作用。
(References):
[1]Zhang X.Three-Dimensional Stability Analysis of Concave Slopes in Plan View[J].Journal Geotechnical Engineering,ASCE,1988,114(6):658-671.
[2]Chugh K A.On the Boundary Conditions in Slope Stability Analysis[J].International Journal for Numerical and Analytical Methods in Geomechanics,2003,27:905-926.
[3]Griffiths D V,Marquez R M.Three-Dimensional Slope Stability Analysis by Elasto-Plastic Finite Elements[J].Geotechnique,2007,57(6):537-546.
[4]方建瑞,许志雄,庄晓莹.三维边坡稳定弹塑性有限元分析与评价[J].岩土力学,2008,29(10):2667-2672.Fang Jianrui,Xu Zhixiong,Zhuang Xiaoying.Appraisal and Analysis of Three-Dimensional Slope Stability Based on Elastoplastic FEM[J].Rock and Soil Mechanics,2008,29(10):2667-2672.
[5]刘红帅,年廷凯,万少石.三维边坡稳定性分析中的边界约束效应[J].吉林大学学报:地球科学版,2010,40(3):638-644.Liu Hongshuai,Nian Tingkai,Wan Shaoshi.Effect of Boundary Constraint Condition on the Stability Analysis of 3DSlope[J].Journal of Jilin University:Earth Science Edition,2010,40(3):638-644.
[6]万少石.涉水边坡稳定性的三维强度折减有限元分析[D].大连:大连理工大学,2009.Wan Shaoshi. Three-Dimensional Slope Stability Analysis by Shear Strength Reduction Finite Element Method(SSR-FEM)Under Drawdown Condition[D].Dalian:Dalian University of Technology,2009.
[7]Wei W B,Cheng Y M,Li L.Three-Dimensional Slope Failure Analysis by the Strength Reduction and Limit Equilibrium Methods[J].Computers and Geotechnics,2009,36:70-80.
[8]Manzari M T,Nour M A.Significance of Soil Dilatancy in Slope Stability Analysis[J].Journal of Geotechnical and Geoenvironmental Engineering,2000,126(1):75-80.
[9]Hibbitt,Karlsson,Sorensen,et al.ABAQUS/Standard User’s Manual;ABAQUS/CAE User’s Manual;ABAQUS Keywords Manual;ABAQUS Theory Manual;ABAQUS Example Problems Manual;ABAQUS Verification Manual[M].[s.l.]:HSK Corporation,2005.
[10]万少石,年廷凯,蒋景彩.边坡稳定强度折减有限元分析中的若干问题[J].岩土力学,2010,31(7):2283-2288.Wan Shaoshi,Nian Tingkai,Jiang Jingcai.Discussion on Several Issues in Slope Stability Analysis Based on Shear Strength Reduction Finite Element Methods[J].Rock and Soil Mechanics,2010,31(7):2283-2288.
[11]郑宏,李春光,李焯芬,等.求解安全系数的有限元法[J].岩土工程学报,2002,24(5):626-628.Zheng Hong,Li Chunguang,Lee Chackfan,et al.Finite Element Method for Solving the Factor of Safety[J].Chinese Journal of Geotechnical Engineering,2002,24(5):626-628.
[12]段庆伟,王玉杰.试论强度折减有限元法变形参数折减的必要性和相应判据[J].水利学报,2008,39(11):1251-1256.Duan Qingwei,Wang Yujie.On the Necessity of Reducing Deformation Parameters for Strength-Reduction FEM and Corresponding Criteria[J].Journal of Hydraulic Engineering,2008,39(11):1251-1256.
[13]Chen Z,Mi H,Zhang F,et al.A Simplified Method for 3DSlope Stability Analysis [J]. Canadian Geotechnical Journal,2003,40(3):675-683.
[14]Chen Z,Wang J,Wang Y,et al.A Three Dimensional Slope Stability Analysis Method Using the Upper Bound Theorem:Ⅱ:Numerical Approaches,Applications and Extensions[J].International Journal of Rock Mechanics & Mining Sciences,2001,38:379-397.
